在人工智能算力需求呈指数级增长的今天，支撑其运行的 AI 芯片正面临着双重挑战：一方面，传统硅基芯片基于冯・诺依曼架构的设计范式逐渐逼近量子物理极限，能耗过高与数据搬运效率低下的问题日益凸显；另一方面，生物神经系统在能效比和并行处理上的天然优势，为芯片架构创新提供了全新的仿生学视角。本文将从底层物理原理与生物信息处理机制出发，系统梳理现有技术瓶颈与前沿探索方向，揭示 AI 芯片从 "硅基逻辑" 向

利用长短时记忆网络（LSTM）捕捉价格序列中的长期依赖关系，预测未来N日收益率。

LSTM通过三个“门”实现对信息的筛选与控制：- **遗忘门（Forget Gate）**：决定丢弃哪些旧信息（如短期噪声）。- **输入门（Input Gate）**：选择接纳哪些新信息（如突破关键均线的信号）。- **输出门（Output Gate）**：控制输出用于预测的信息（如收益率的非线性组合）。

bsidian：从笔记工具到全能生态，重新定义数字时代的知识管理与创作范式

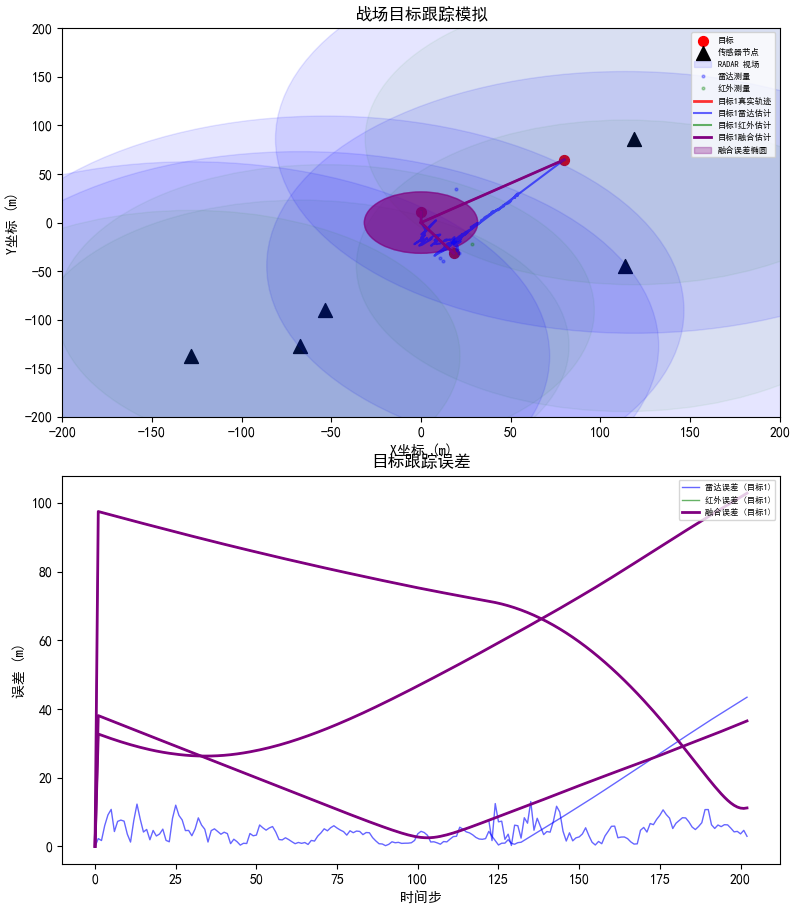
在复杂空战环境中，单一传感器（如雷达或红外）受限于探测精度、视角盲区和电磁干扰，难以提供可靠的目标跟踪数据。本文通过构建六维目标运动模型，结合卡尔曼滤波算法实现多传感器数据融合，解决目标状态估计的噪声抑制与轨迹平滑问题。并用Python基于相关理论构建多传感器融合仿真应用，在推动传感器融合技术在复杂动态环境中的实际应用有一定借鉴意义。

文章聚焦混合专家模型（MoE），阐述其通过“分治策略”将大模型拆解为专精“专家模块”，利用门控网络动态路由实现稀疏激活，突破传统稠密模型的算力与参数规模瓶颈。内容涵盖架构原理（专家网络与门控机制、对比稠密模型的计算效率优势）、训练策略（数据分片引导专家分工、负载均衡技术、分布式训练优化及成本对比）、大规模数据处理优势（参数扩展能力、多任务自适应、翻译/生成等场景性能提升），并分析其模型复杂度、路由

通过deepseek调用pollinations API 生成图片的方法

本地化部署Deepseek关于Ollama 安全加固方案（新手易学）

Flask 个人开发者常见需求特征、应用实例及技术栈

文章聚焦混合专家模型（MoE），阐述其通过“分治策略”将大模型拆解为专精“专家模块”，利用门控网络动态路由实现稀疏激活，突破传统稠密模型的算力与参数规模瓶颈。内容涵盖架构原理（专家网络与门控机制、对比稠密模型的计算效率优势）、训练策略（数据分片引导专家分工、负载均衡技术、分布式训练优化及成本对比）、大规模数据处理优势（参数扩展能力、多任务自适应、翻译/生成等场景性能提升），并分析其模型复杂度、路由