一、有偏估计和无偏估计假设我们测量了变量xxx，测得的结果是x1,x2,⋯ ,xnx_1,x_2,\cdots,x_nx1​,x2​,⋯,xn​。令xˉ\bar xxˉ是它们的算术平均值，μ\muμ是xxx的真实值。我们使用标准（偏）差（Standard Deviation）来度量数据分布的分散程度。标准差越大，数据分布越离散，反之越集中。我们在小学/初中学过标准差的计算公式σ=∑i=1N(xi−

这里采用工科数学分析中对闭包的定义。前置知识：定义 设AAA是RnR^nRn中的一个点集，a∈Rna\in R^na∈Rn。若∃A\exists A∃A中的点列{xn}\{x_n\}{xn​}（xk≠a,k=1,2,…x_k\ne a,k=1,2,\dotsxk​​=a,k=1,2,…）使得lim⁡k→∞xk=a\lim \limits_{k\to\infty} x_k=ak→∞lim​xk​=

我们需要考虑三个坐标系：1. 世界坐标系；2. 相机坐标系；3. 图像坐标系。

在上一篇文章中我们介绍了在两个照相机像平面共面的情况下如何计算深度：深度与景物在图片中的位移成反比。这篇文章我们讨论更一般的情形，像平面不必共面，甚至不必平行。假设两个相机的内参（intrinsics）都是标定（calibrate）过的。

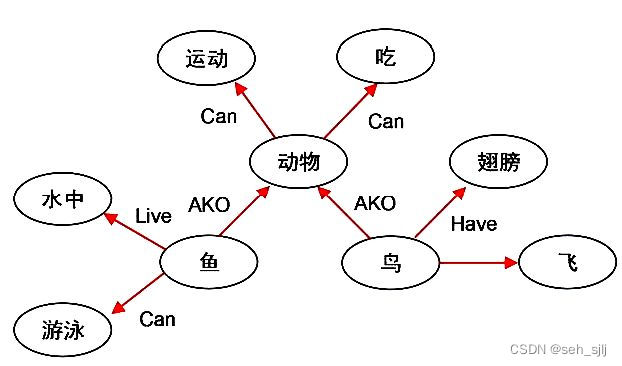
然后对三元组的数据进行知识融合，主要是实体对齐，以及和数据模型进行结合，经过融合之后，会形成标准的数据表示,为了发现新知识，可以依据一定的推理规则，产生隐含的知识，所有形成的知识经过一定的质量评估，最终进入知识图谱。知识图谱是一种语义网络（Semantic Network）的知识库，可以构建庞大的知识网络，包含世间万物构成的实体以及它们之间的关系，图文并茂地展现知识方方面面的属性，让人们更便捷地获

启发式搜索（Heuristic Search）：利用启发方式获得的领域知识，通过限定搜索深度或者限定搜索宽度来缩小问题空间，避开没有结果的搜索路径，也称有信息搜索

../aten/src/ATen/native/cuda/IndexKernel.cu:92: operator(): block: [0,0,0], thread: [15,0,0] Assertion `index >= -sizes[i] && index < sizes[i] && "index out of bounds"` failed.RuntimeError: CUDA error

一、格林公式二、平面线积分与路径无关的条件+无旋场、保守场、有势场三、高斯公式+散度四、斯托克斯公式+旋度五、重要的特殊向量场1. 无旋场（基于斯托克斯公式）2. 无源场（基于高斯公式）3. 调和场...

1. 检查你的网络连接是否可用。2. 如果可用，那么接下来关闭Windows防火墙。对于Win10，再任务栏里输入“防火墙”：点击“防火墙和网络保护”，进入如下页面：分别点击“域网络”、“专用网络”和“公用网络”，下图以“域网络”为例：点击这个按钮，使其变为“关”：在随后弹出的窗口（如果有的话）点击“是”。所有三个防火墙都关完后重新启动Matlab安装程序，多试几次，如果出现提示输入电子邮件的页面

吸收率：(1) A∨(A∧B)⇔A(1)\ A\lor(A\land B)\Leftrightarrow A(1) A∨(A∧B)⇔A(2) A∧(A∨B)⇔A(2)\ A\land(A\lor B)\Leftrightarrow A(2) A∧(A∨B)⇔A证明： 先证明这两个定律等价。由(1)(1)(1)：A∨(A∧B)⇔(A∨A)∧(A∨B)⇔A∧(A