
简介
该用户还未填写简介
擅长的技术栈
可提供的服务
暂无可提供的服务
Dependencies下爆红线、plugin爆红,比如spring-boot-maven-plugin红色
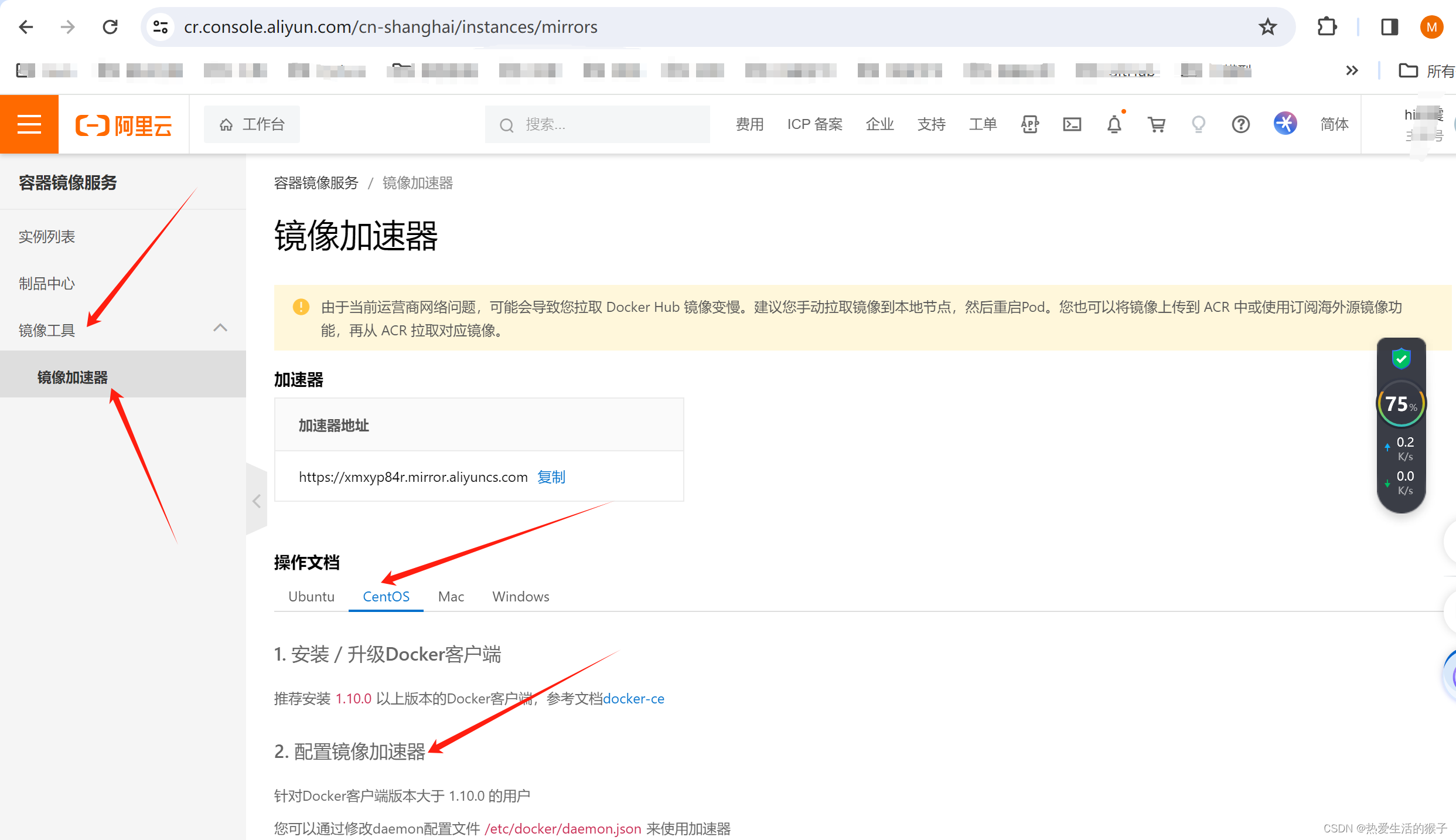
Error response from daemon: Get "https://registry-1.docker.io/v2/": net/http: request canceled (Client.Timeout exceeded while awaiting headers)、docker国内阿里云镜像配置、docker pull拉取失败
一个完整的神经网络训练流程详解

【概念+实例】一文搞懂机器学习、深度学习中的准确率、精确率、召回率、F1分数

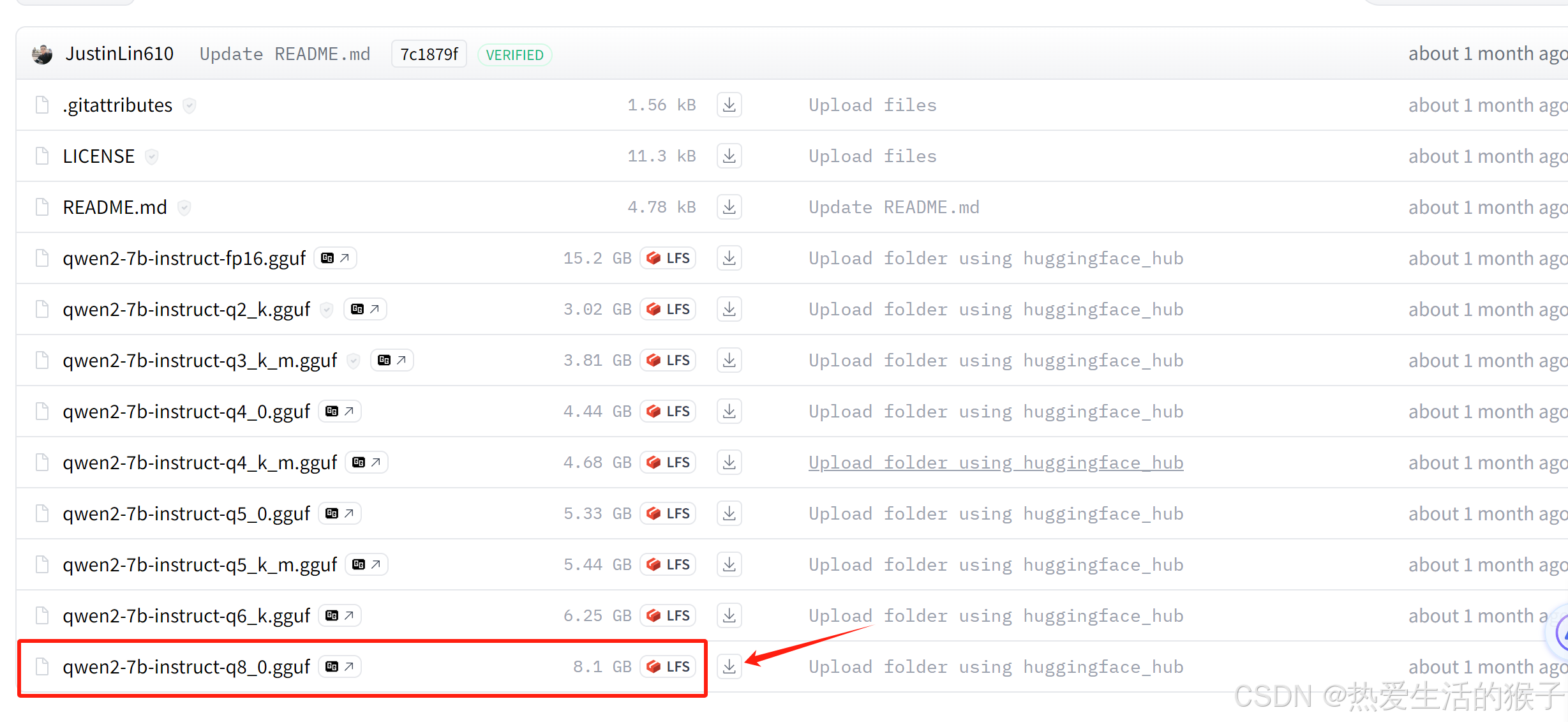
先附上llama.cpp的github地址:https://github.com/ggerganov/llama.cpp,build地址:https://github.com/ggerganov/llama.cpp/blob/master/docs/build.md。如果需要在内网服务器中安装,可以下载llama.cpp的源码文件或二进制文件,下载地址:https://github.com/gge

【内网Tesla T4_16G为例】超详细安装部署ollama、加载uugf格式大模型qwen2、chatglm3及大模型的使用
摘要: 时间复杂度和空间复杂度是衡量算法效率的核心指标。时间复杂度反映算法执行时间随输入规模(n)的增长趋势,常见类型包括O(1)、O(n)、O(n²)等,可通过循环或递归的嵌套层数判断。空间复杂度衡量算法运行中额外占用的内存,如变量、数组或递归栈的深度。判断时需注意:输入本身不计入空间复杂度,仅统计额外创建的存储结构。口诀总结:时间看操作次数,空间看额外内存。例如,单层循环为O(n),数组副本为
Word2Vec的使用,含示例——包括使用预训练Word2Vec模型和自训练Word2Vec模型

【内网Tesla T4_16G为例】超详细安装部署ollama、加载uugf格式大模型qwen2、chatglm3及大模型的使用

一个完整的神经网络训练流程详解











