本文详细介绍使用SPSS软件进行曲线回归的理论基础、操作步骤及结果分析。非线性关系本质是指不仅形式上呈非线性关系，而且也无法通过变量变换转化为线性关系，最行线性回归分析，建立线性模型。本实验针对本质线性模型进行。曲线估计的基本步骤：(1)绘制因变量与自变量的散点图，大致确定非线性关系的类型。(2)选择多个曲线回归预测模型，估计参数。(3)利用输出的检验统计量对回归预测模型进行各项显著性检验。(4)

本文详细介绍使用SPSS软件进行简单线性回归的理论基础、操作步骤及结果分析。回归分析是定量反映数值型变量之间明显存在的相关关系的一种统计推断方法。回归分析根据自变量的多少可分为简单回归分析和多元回归分析，根据关系类型可分为线性回归分析和非线性回归分析。简单线性回归分析就是在一个因变量与一个自变量之间进行的线性相关关系的统计推断。分析散点图、残差图判断线性关系是否真实存在，以及模型假设是否成立。根据

文章以spss26.0为基础，借鉴李永江老师等人的spss应用教程一书，包含数据文件的合并、数据排秩、个案加权的基本数据处理方法，包含各步骤截图，内容详细明了。

文章以spss26.0为基础，借鉴李永江老师等人的spss应用教程一书，包含结构重组、文件拆分、数据分组的基本数据处理方法，包含各步骤截图，内容详细明了。

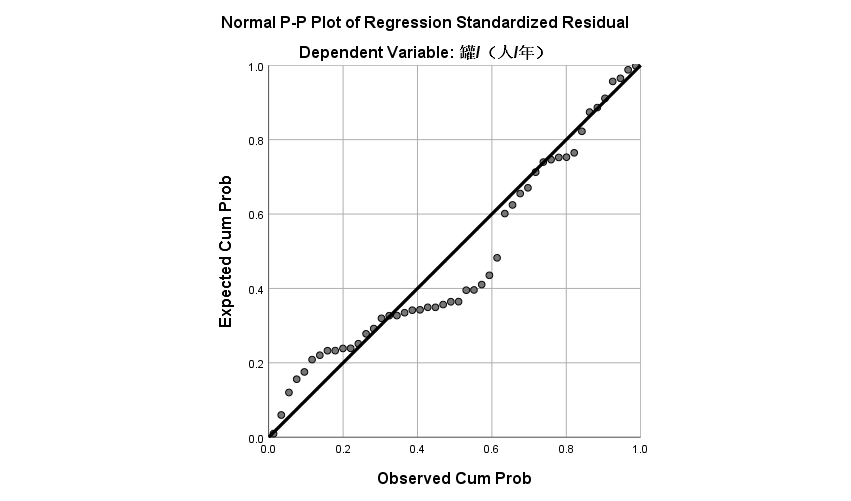
本文详细介绍使用SPSS软件进行多元线性回归的理论基础、操作步骤及结果分析。多元线性回归模型是指含有多个自变量的线性回归模型，用于解释因变量与其他多个自变量之间的线性关系。多元线性回归分析的基本步骤(1)确定因变量与自变量，并初步设定多元线性回归方程。(2)估计参数，确定估计多元线性回归方程。(3)利用检验统计量对回归预测模型进行各项显著性检验。(4)检验通过后，可利用回归模型进行预测，分析评价预

文章以spss26.0软件为基础，借鉴李永江老师等人的spss应用教程一书，包含spss软件的数据转置、样本筛选、分类汇总的基本数据处理方法。

将excel表处理成如下形式（预测指标放在最后一列），然后将excel数据另存为txt形式，可以在python中引用。其中，solver参数可选“lbfgs（优化器，小样本适用）、sgd（随机梯度下降）、adam（默认，大样本适用）”其中安装sklearn库前需要安装numpy、scipy、matplotlib库。（年份是我随便写的，实际应该是1990-2012，在代码画图时可以用到）pip in

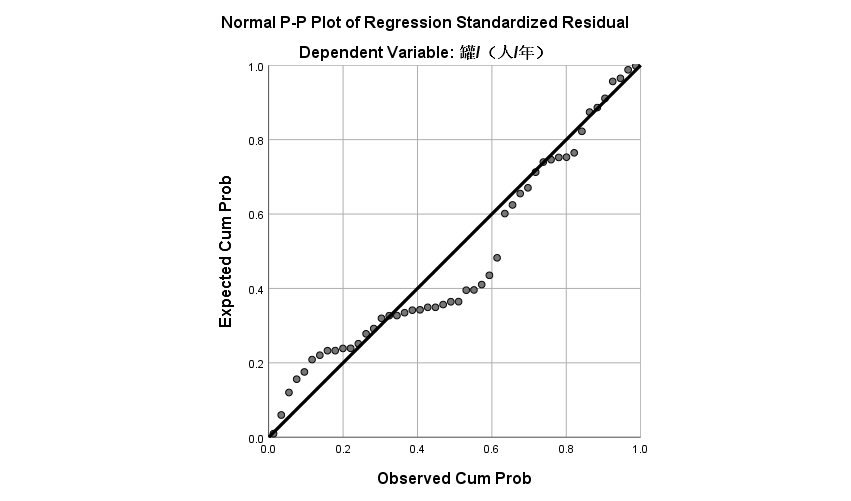
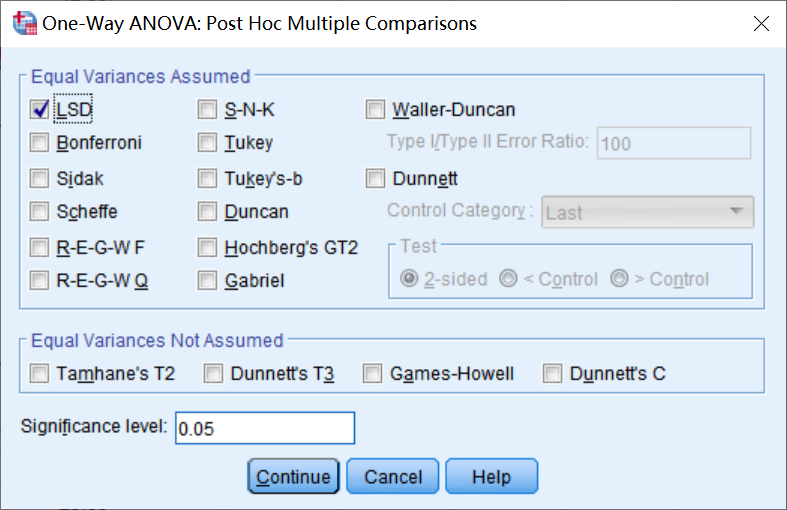
本文详细介绍使用SPSS软件进行单因素方差分析的理论基础、操作步骤及结果分析。方差分析是检验两个或两个以上的样本均值之间的差异是否具有统计学意义的一种方法，目的是推断两个或两个以上的总体均值是否相同。它所研究的是分类型自变量对数值型因变量的影响。当只涉及一个分类型自变量时，该分析称为单因素方差分析；涉及两个或两个以上的分类型自变量时，则称为多因素方差分析。包含例题的详细操作步骤及结果分析，保姆级教

本文详细介绍使用SPSS软件进行协方差的理论基础、操作步骤及结果分析。协方差分析是传统方差分析方法的一种延续。不论是单因素方差分析，还是多因素方差分析，都不曾考虑协变量的存在，但协变量却会对因变量产生显著影响。为了更准确地研究自变量(可控制变量)不同水平对因变量的影响，需要考虑协变量在其中的影响程度。这就是协方差分析所要解决的问题。

本文详细介绍使用SPSS软件进行多因素方差分析的理论基础、操作步骤及结果分析。方差分析中当涉及两个或两个以上的分类型自变量时，则需要进行多因素方差分析。进行多因素方差分析时，要首先确定因变量和若干个自变量，其次分析数值型因变量的方差，最后分别比较因变量总离差平方和各部分所占比例，进而推断自变量以及自变量的交互作用是否给因变量带来了显著影响。包含例题的详细操作步骤及结果分析，保姆级教程包会。