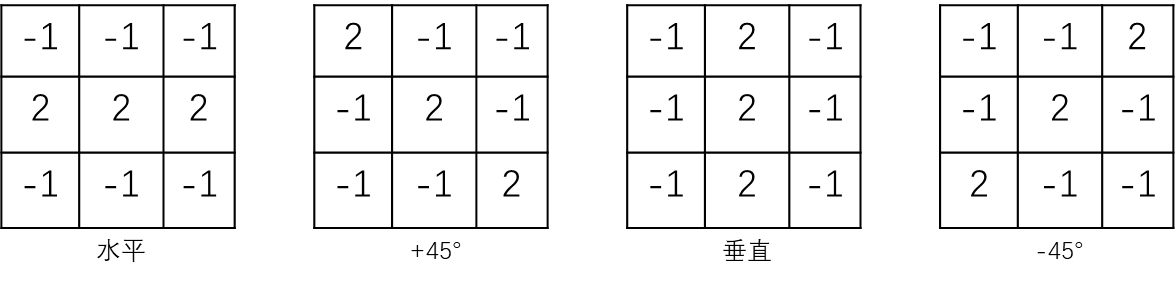
一、线特征提取1.1 模板线检测使用模板在一幅图像上移动，他会对特定方向上的（一个像素宽）线响应强烈。下面是常见检测模板：1.2 边缘检测边缘检测的基本思想是使用如下两个准则之一找到图像中快速变换的位置：1. 寻找灰度的一阶导数的幅值大于某个阈值的位置2. 寻找灰度的二阶导数有零交叉的位置matlab提供的函数：[g,t]=edge(f,'method',paramters)1.2.1 Sobel

项目场景：读取一幅二进制(uint16)raw原始图像并对其进行显示，以便后续的图像处理工作matlab代码：fid = fopen("F:\jihe0001.raw",'r'); %默认是小端存储data = fread(fid,[2048 12294],'uint16');%大小是2048*12294，取第一个通道data1 = mat2gray(data); %mat2gray将double

matlab最优化问题提纲以及工具箱

一、游戏策划1、游戏介绍  游戏背景是在火星的上空，主角和敌人是不同的太空飞行器，敌人迎面向主角飞来，主角通过射击消灭敌人来获得分数。如果主角战败，则游戏结束。2、游戏UI  屏幕上显示主角生命值以及得分。如果游戏结束，屏幕上显示“游戏结束“，同时显示“再来一次”按钮。按ESC键，游戏会处于暂停状态，显示“继续游戏”，“退出游戏”。3、主角  主角有三条性命，被敌人撞击一次性命直接清零，被敌方子弹

使用nuitka打包python的pyqt5项目详细过程介绍以及遇见bug解决方法

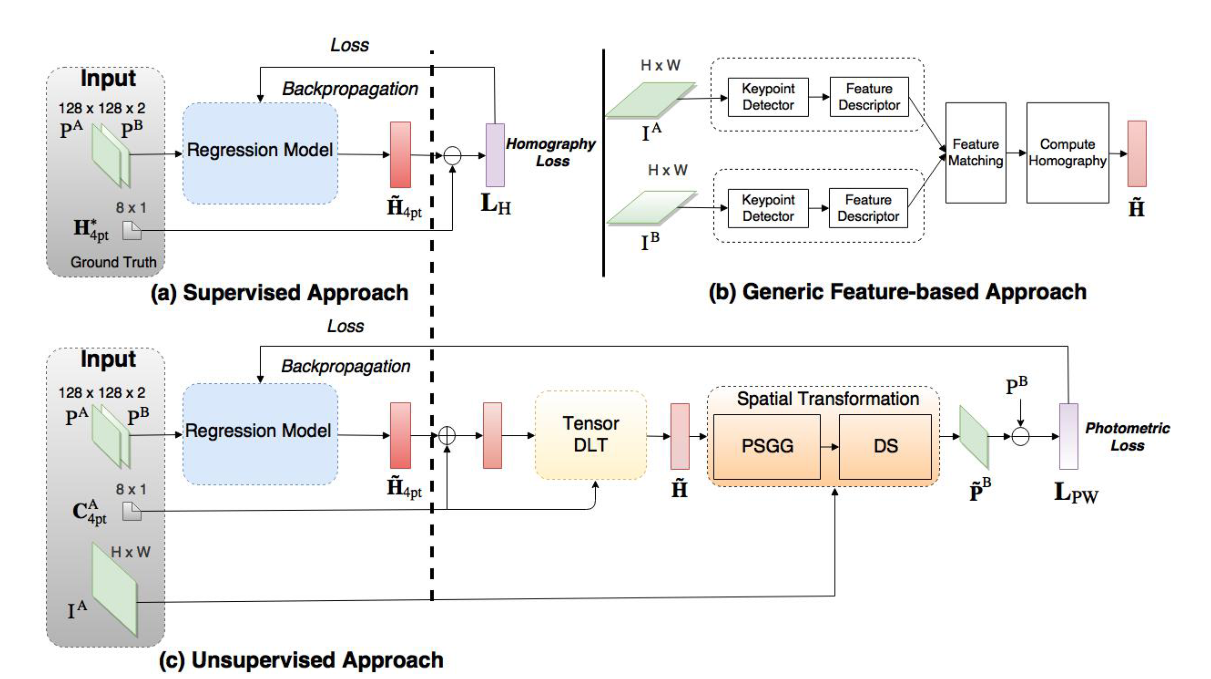
单应性是一个平面的两个图像之间从不同角度的映射。它们在机器人和计算机视觉应用中发挥着重要作用，例如图像拼接[1]、单目SLAM[2]、3D相机姿势重建[3]和虚拟漫游[4]、[5]。例如，单形文字适用于由任意移动摄像机远距离观看的场景[6]，这是UA V图像中遇到的情况。然而，要在空中多机器人环境中良好工作，单应性估计算法需要可靠和快速。单应性估计的两种传统方法是直接方法和基于特征的方法[7]。

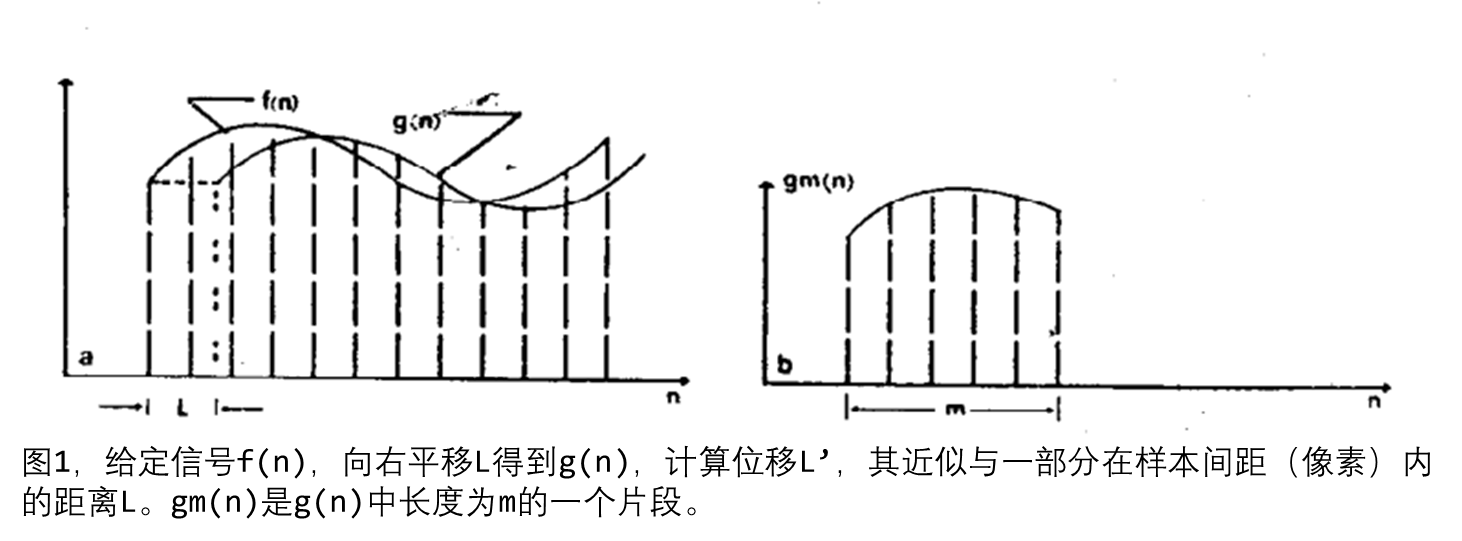
摘要本文分析了四种能以亚精确度重新排列图像的算法，分别是相关插值（correlation interpolation）、强度插值（intensity interpolation）、微分方法（differential method）和相位相关（phase correlation）。详细介绍了亚像素配准问题。影响配准的主要因素是插值函数，采样频率，每个像素的位数，图像的灰度范围(?)（frequenc

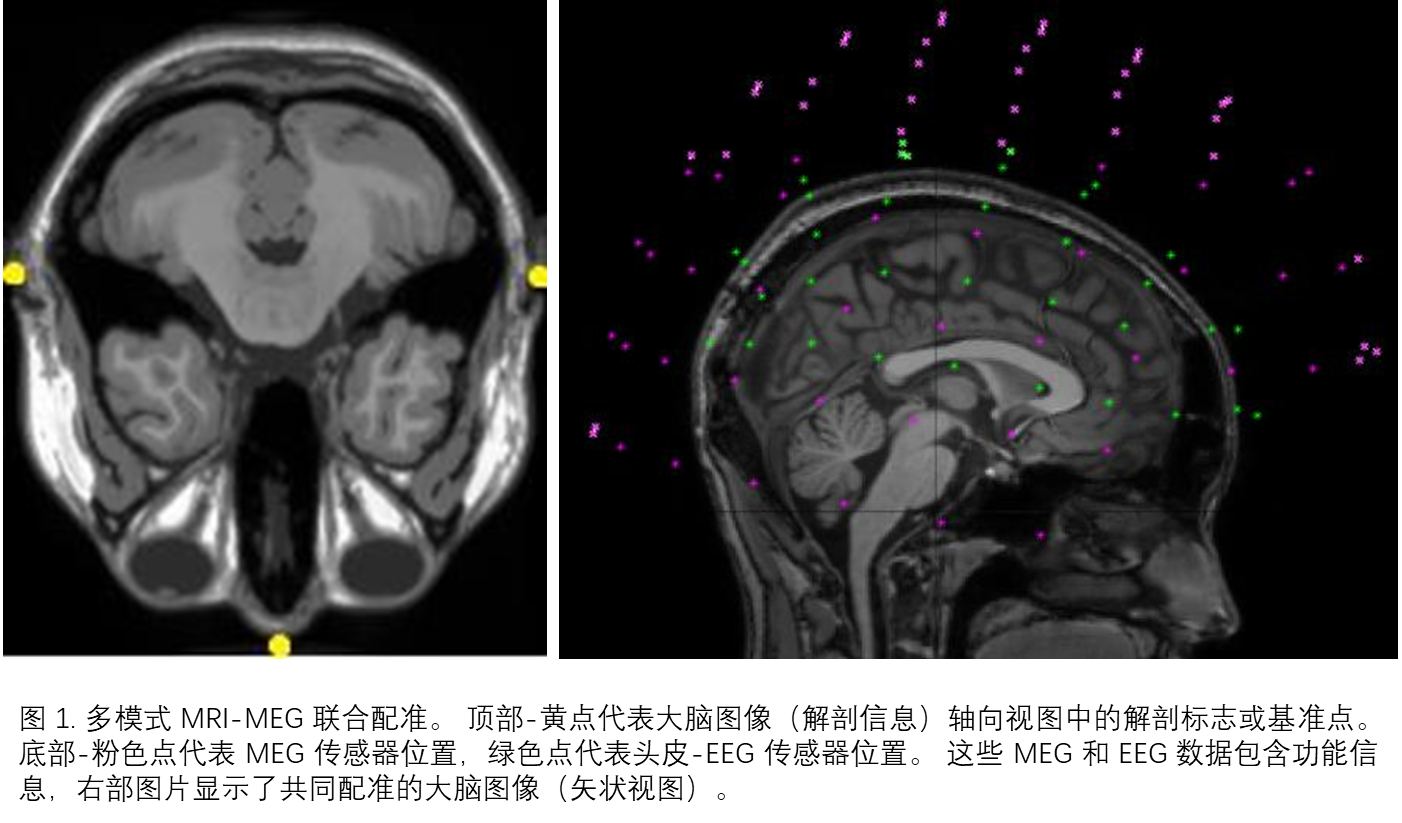
摘要图像配准是参考特定图像，将同一场景的两个或多个图像对齐的过程。图像配准可应用于医学、遥感和计算机视觉。 本文详细回顾了几种方法，并根据它们的贡献和缺点进行了相应分类。 还讨论了图像配准过程的主要步骤，提出了不同的性能指标来确定配准质量和准确性，以及提出了未来研究的范围。关键词——图像配准、分类、贡献、缺点、性能指标、配准质量、准确性、未来研究。一、引言图像配准： 被解释为将同一场景的两个或多个

一、基于灰度的模板匹配参考文章：https://blog.csdn.net/hujingshuang/article/details/477595791.1 MAD算法平均绝对差算法（Mean Absolute Differences，简称MAD算法）。它是Leese在1971年提出的一种匹配算法。算法的思想简单，具有较高的匹配精度。算法思路： 选模板Rm×nR_{m×n}Rm×n​，从搜索图SM

一、超定方程组超定方程组是指方程个数大于未知量个数的方程组。对于方程组Ax=bAx=bAx=b，AAA为n×m矩阵，如果R列满秩，且n>m。则方程组没有精确解，此时称方程组为超定方程组。在实验数据处理和曲线拟合问题中，求解超定方程组非常普遍。比较常用的方法是最小二乘法。如果有向量xxx使得下式的值达到最小，则称 xxx为上述超定方程的最小二乘解。二、矩阵形式的最小二乘法最小二乘法问题：E(x