看了网上很多答案，包括安装插件，如：nbextensions但是没起作用还看到说是因为其基于ipython，所以我又update了ipython，还是无效最后我发现，每当我在jupyter notebook里面按tab键的时候，terminal（mac的命令行）会出现错误提示，TypeError: __init__() got an unexpected keyword argument ‘col

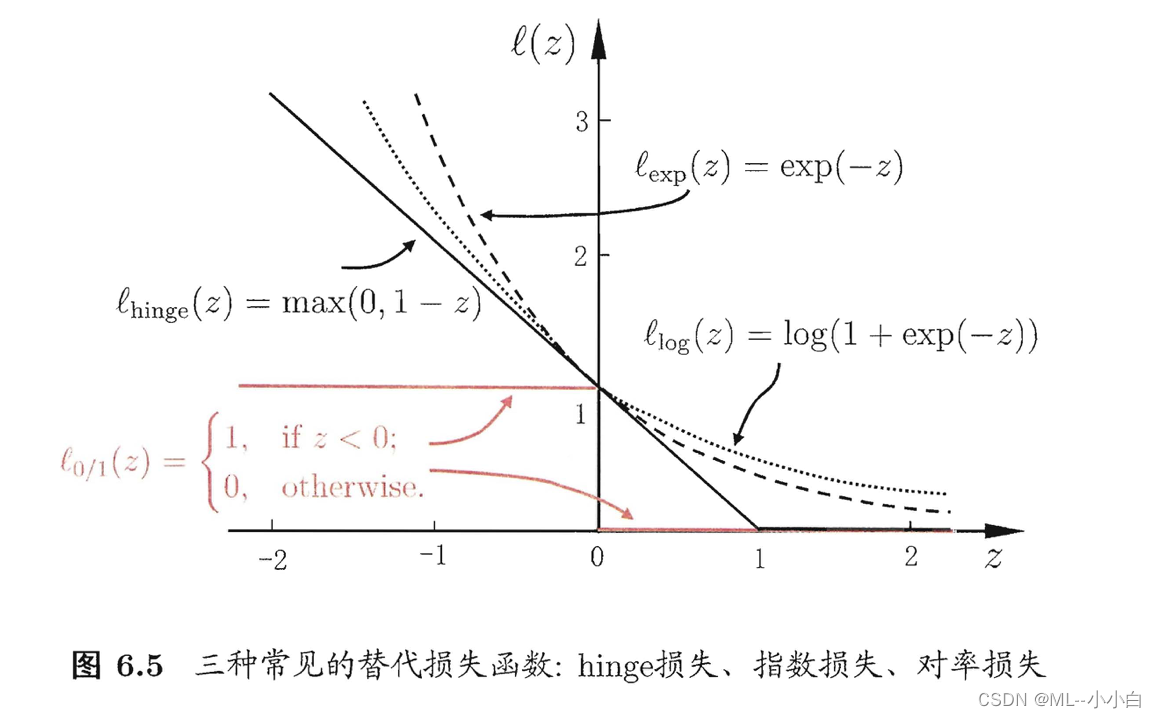
支持向量机（Support Vector Machine，SVM）的主要目的就是在特征空间中找到距离正反例最远的分离超平面，由于是“最远”因此与上一章感知机里初值敏感，由误分类点修正最后得到的“初值敏感”的超平面不同，对于线性可分的（linearly separable）数据集，SVM确定的分离超平面是唯一的，超平面上的点可以用“平面”方程表示：wTx+b=0\boldsymbol{w}^{\ma

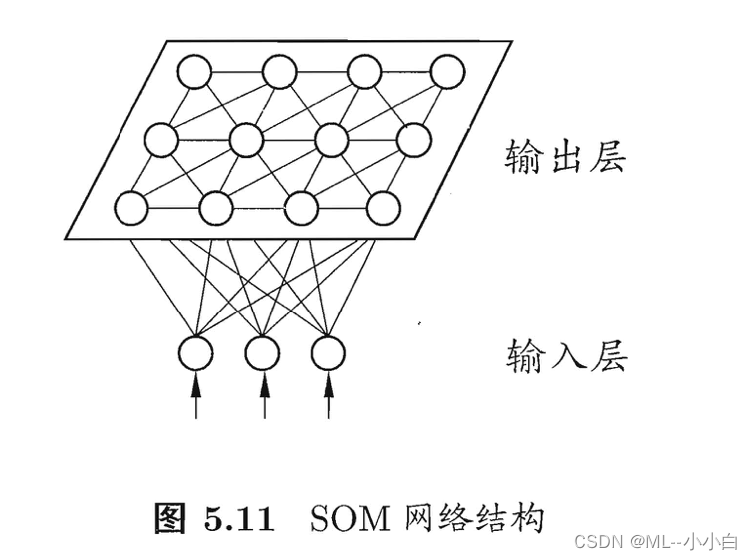
神经元（neuron，亦称unit）其实就是一个小型的分类器，其将从其他神经元输入的信息带权重连接进入，然后比较其与阈值的相对大小，并将差异通过激活函数（activationfunction），决定其是否被”激活“/”兴奋“。这种神经元的抽象模型1943年就被提出了，被两位提出者名字首字母命名为”M-P神经元模型“。最常使用的激活函数为Sigmoid（亦称squashing）函数。...

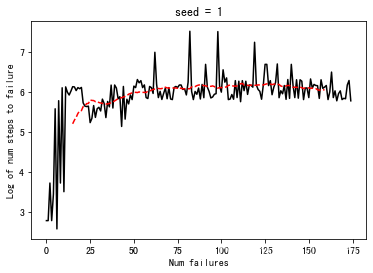
6. Reinforcement Learning: The inverted pendulum首先写出simulator（作业中已提供，直接复制过来）：import matplotlib.pyplot as pltimport matplotlib.patches as patchesfrom math import sin, cos, piclass CartPole:def __init__

主要是一个递归过程。

EM算法 K均值聚类 高斯混合模型

6. Reinforcement Learning: The inverted pendulum首先写出simulator（作业中已提供，直接复制过来）：import matplotlib.pyplot as pltimport matplotlib.patches as patchesfrom math import sin, cos, piclass CartPole:def __init__

第九章思维导图总结：import numpy as np9.1y = np.array([[1, 1, 0, 1, 0, 0, 1, 0, 1, 1]]).Tm = y.shape[0]theta = np.array([[0.46, 0.55, 0.67]]).T# initializationfor i in range(100):theta_old = theta.copy()q_theta

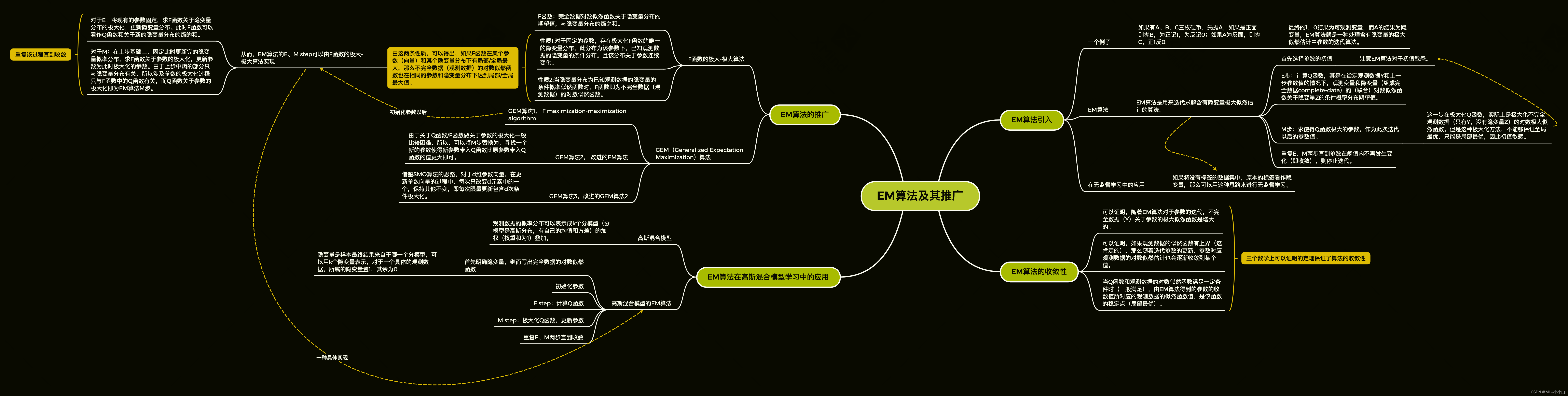
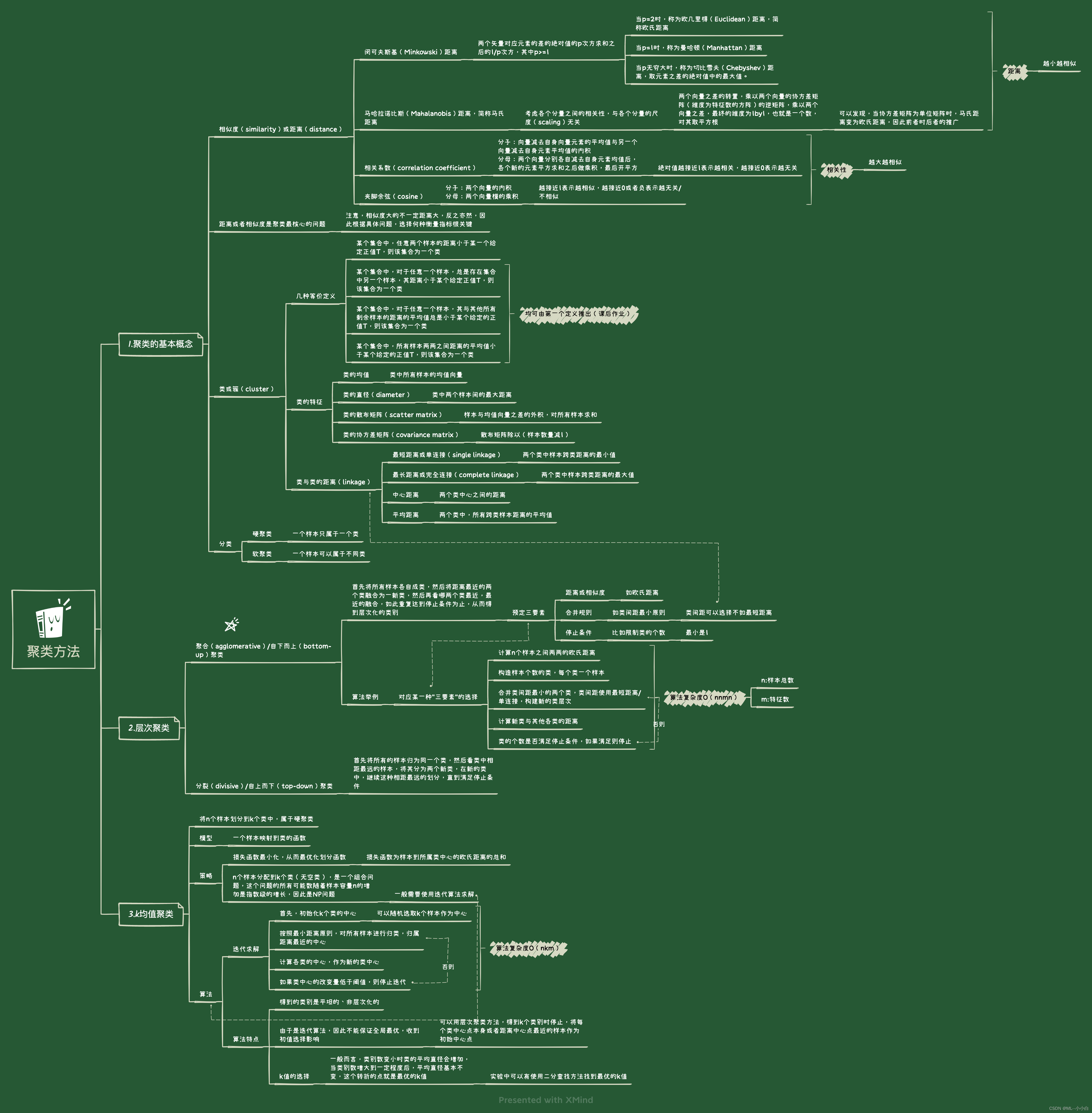
思维导图：14.1试写出分裂聚类算法，自上而下地对数据进行聚类，并给出其算法复杂度。i. 计算n个样本两两之间的距离，并将所有样本看作一个类，将样本间最大距离作为类直径；ii. 对于类直径最大的类，将其中相距最远，也就是距离为类直径的两个样本分成两个新类，该类其他样本就近（相对于那两个选中的样本）归于两个类之一；iii. 如果类别个数达到停止条件（预设的分类书）则停止，否则回到ii.步骤。模型复杂

代码主要参考《python机器学习及实践》一书分类学习Logistics 回归 和 SGD分类器模型import pandas as pdimport numpy as npcolumn_names = ['Sample code number', 'Clump Thickness', 'Uniformity of Cell Size','Uniformity of Cell Shape', 'M