SVM超平面计算例题

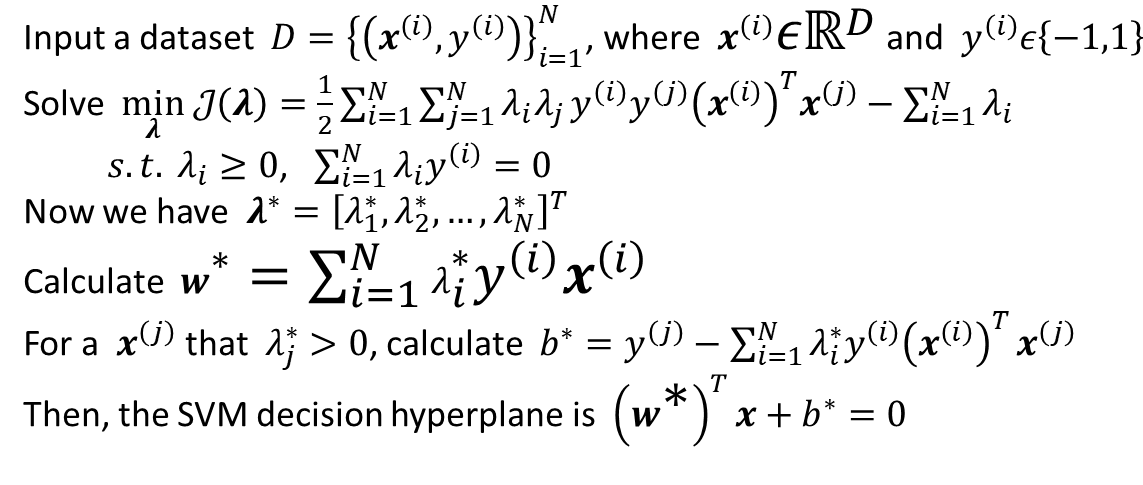
主页：https://lingjie0206.github.io/papers/NeuS/论文：https://arxiv.org/abs/2106.10689代码：https://github.com/Totoro97/NeuS给定一组3D对象的摆姿势图像{Ik}\{I_k\}{Ik​}，我们的目标是重建其表面SSS。表面由神经隐式SDF的零级集表示。为了学习神经网络的权重，我们开发了一种新颖的

SVM超平面计算例题

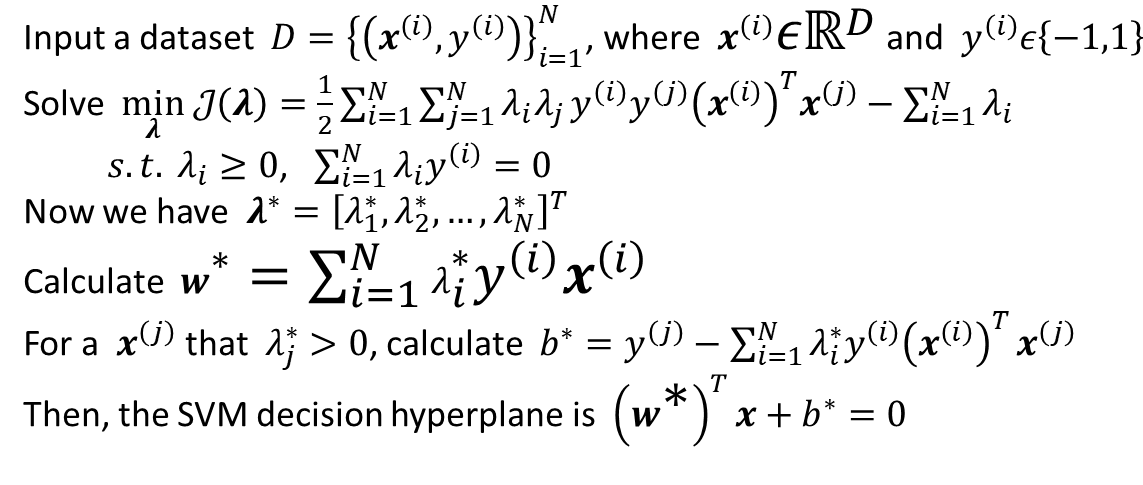
译文：我们使用神经辐射场 (nerf) 从大规模的视觉捕获中构建交互式3D环境，这些捕获跨越建筑物，甚至是主要从无人机收集的多个城市街区。与单个对象场景 (传统上对nerf进行评估) 相反，我们的规模提出了多个挑战，包括 (1) 需要对具有不同照明条件的数千个图像进行建模，每个图像仅捕获场景的一小部分，(2) 令人望而却步的大模型容量，使其无法在单个GPU上进行训练，并且 (3) 快速渲染将实现交

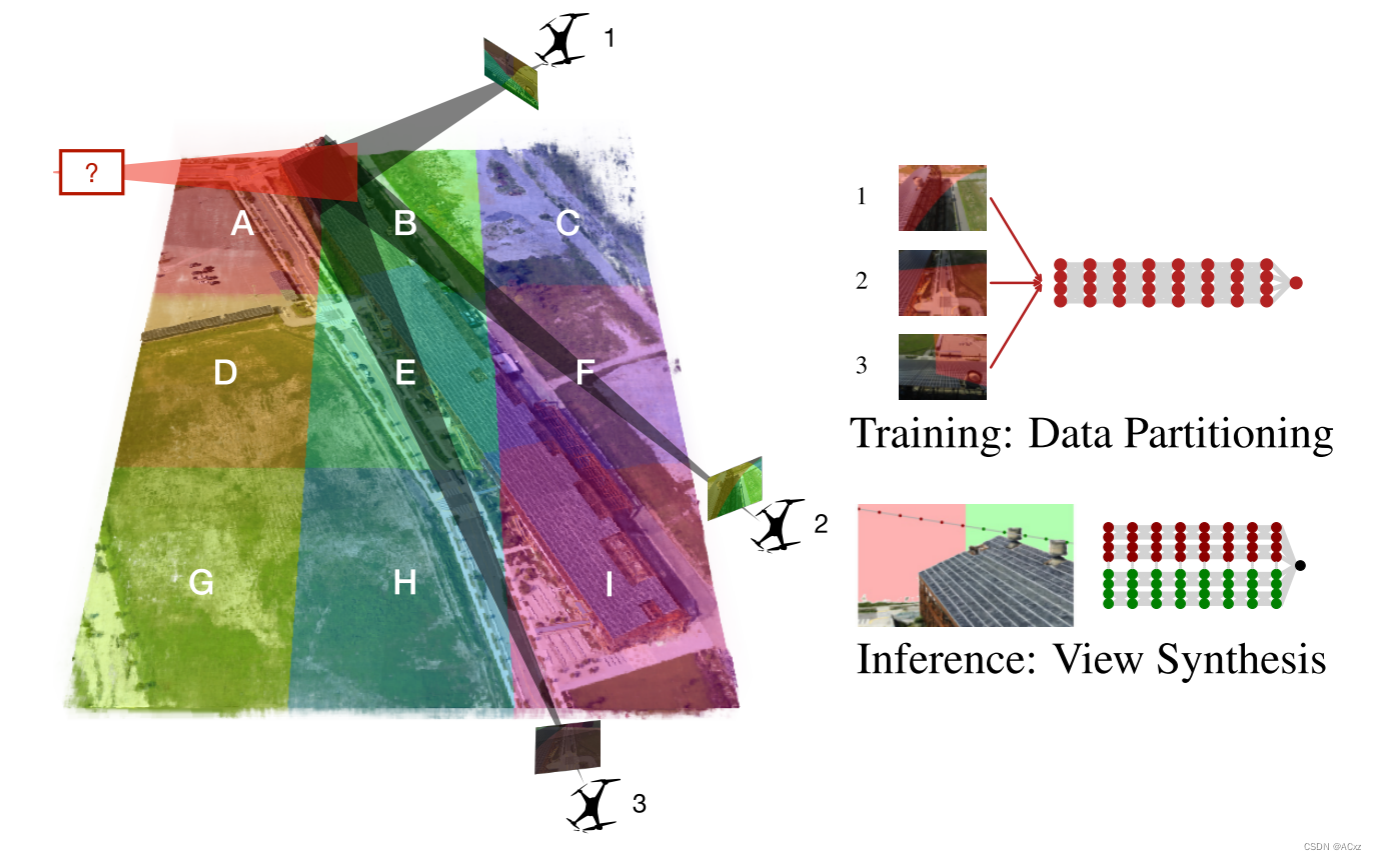
译文：我们使用神经辐射场 (nerf) 从大规模的视觉捕获中构建交互式3D环境，这些捕获跨越建筑物，甚至是主要从无人机收集的多个城市街区。与单个对象场景 (传统上对nerf进行评估) 相反，我们的规模提出了多个挑战，包括 (1) 需要对具有不同照明条件的数千个图像进行建模，每个图像仅捕获场景的一小部分，(2) 令人望而却步的大模型容量，使其无法在单个GPU上进行训练，并且 (3) 快速渲染将实现交

数组创建创建数组有 6 种通用机制：从其他 Python 结构（即列表和元组）转换内在的 NumPy 数组创建函数（例如 arange、1、0 等）复制、加入或改变现有数组从磁盘读取数组，无论是标准格式还是自定义格式通过使用字符串或缓冲区从原始字节创建数组特殊库函数的使用（例如，随机）您可以使用这些方法来创建 ndarrays 或Structured arrays。将 Python 序列转换为 N

k-means简介k-means 算法在不带标签的多维数据集中寻找确定数量的簇。最优的聚类结果需要符合以下两个假设。“簇中心点”（cluster center）是属于该簇的所有数据点坐标的算术平均值。一个簇的每个点到该簇中心点的距离，比到其他簇中心点的距离短。这两个假设是k-means 模型的基础，后面会具体介绍如何用该算法解决问题。先通过一个简单的数据集，看看k-means 算法的处理结果。首先

举例import networkx as nximport matplotlib.pyplot as plt我们先通过nx.erdos_renyi_graph(10, 0.15)方法随机生成图像er = nx.erdos_renyi_graph(10, 0.15)nx.draw(er,node_size=300,with_labels = True,pos = nx.spring_layout(e

决策树与随机森林下面将介绍另一种强大的算法——无参数算法随机森林。随机森林是一种集成方法，通过集成多个比较简单的评估器形成累积效果。这种集成方法的学习效果经常出人意料，往往能超过各个组成部分的总和；也就是说，若干评估器的多数投票（majority vote）的最终效果往往优于单个评估器投票的效果！后面将通过示例来演示，首先还是导入标准的程序库：import requestsurl = 'https

高斯混合模型k-means 聚类模型非常简单并且易于理解，但是它的简单性也为实际应用带来了挑战。特别是在实际应用中，k-means 的非概率性和它仅根据到簇中心点的距离来指派簇的特点将导致性能低下。这一节将介绍高斯混合模型，该模型可以被看作是k-means思想的一个扩展，但它也是一种非常强大的聚类评估工具。还是从标准导入开始：%matplotlib inlineimport matplotlib.