连通图：在无向图中，若从顶点v1到顶点v2有路径，则称顶点v1与顶点v2是连通的。如果图中任意一对顶点都是连通的，则称此图为连通图强连通图：在有向图中，若在每一对顶点vi和vj之间都存在一条从vi到vj的路径，也存在一条从vj到vi的路径，则称此图是强连通图生成树：一个连通图的最小连通子图称作该图的生成树。有n个顶点的连通图的生成树有n个顶点和n-1条边连通图中的每一棵生成树从其中删去任何一条边，

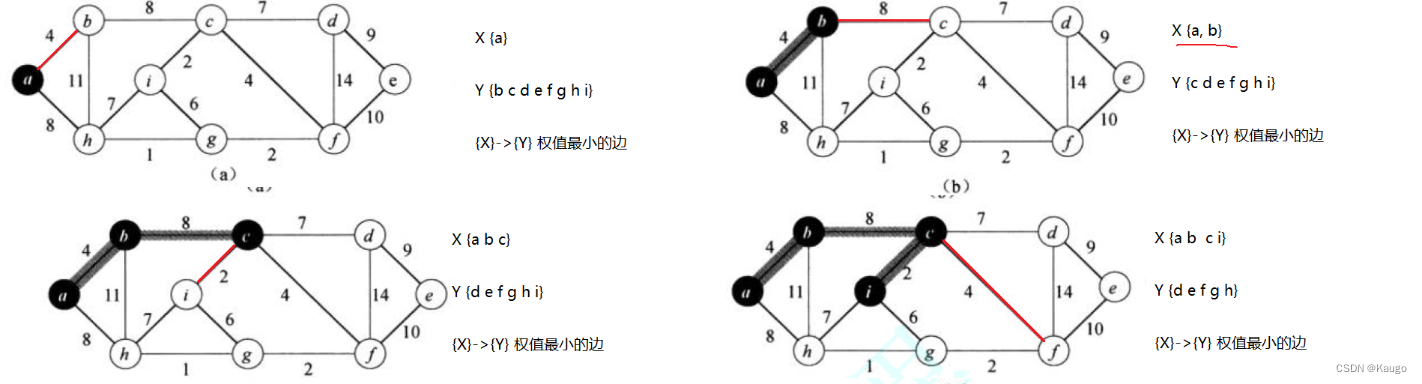
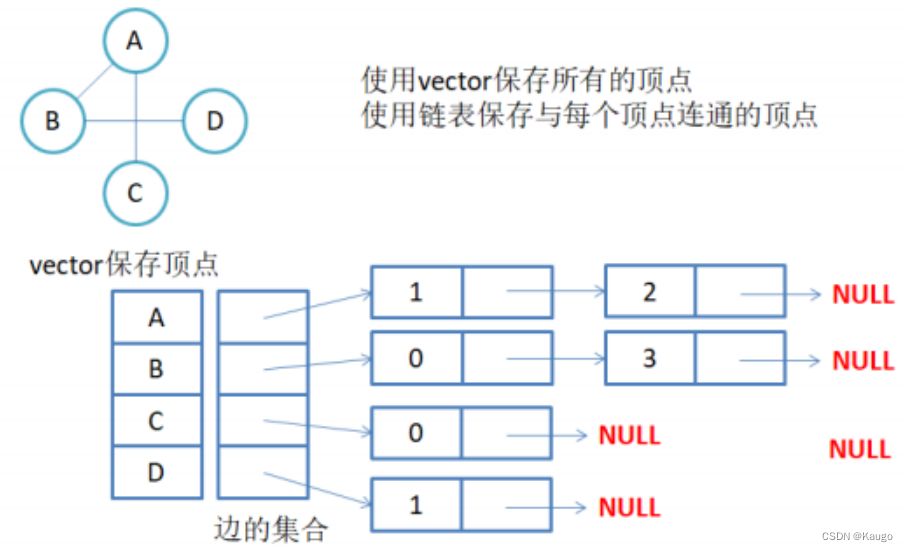
图是由顶点集合及顶点间的关系组成的一种数据结构：G = (V， E)，其中：顶点集合V = {x|x属于某个数据对象集}是有穷非空集合；E = {(x,y)|x,y属于V}或者E = {|x,y属于V && Path(x, y)}是顶点间关系的有穷集合，也叫做边的集合。完全图：在有n个顶点的无向图中，若有n * (n-1)/2条边，即任意两个顶点之间有且仅有一条边，则称此图为无向完全图，比如上图G

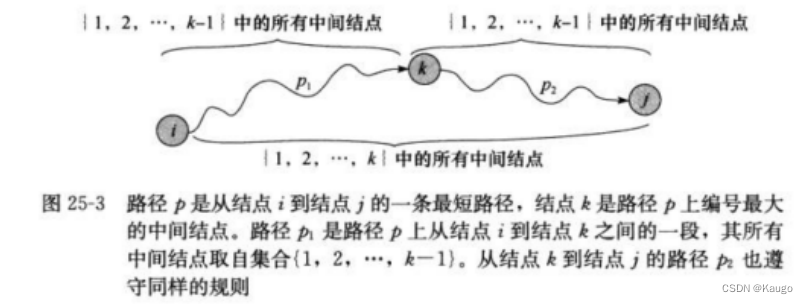
最短路径问题：从在带权有向图G中的某一顶点出发，找出一条通往另一顶点的最短路径，最短也就是沿路径各边的权值总和达到最小。单源最短路径问题：给定一个图G = ( V ， E ) G=(V，E)G=(V，E)，求源结点s ∈ V s∈Vs∈V到图中每个结点v ∈ V v∈Vv∈V的最短路径。

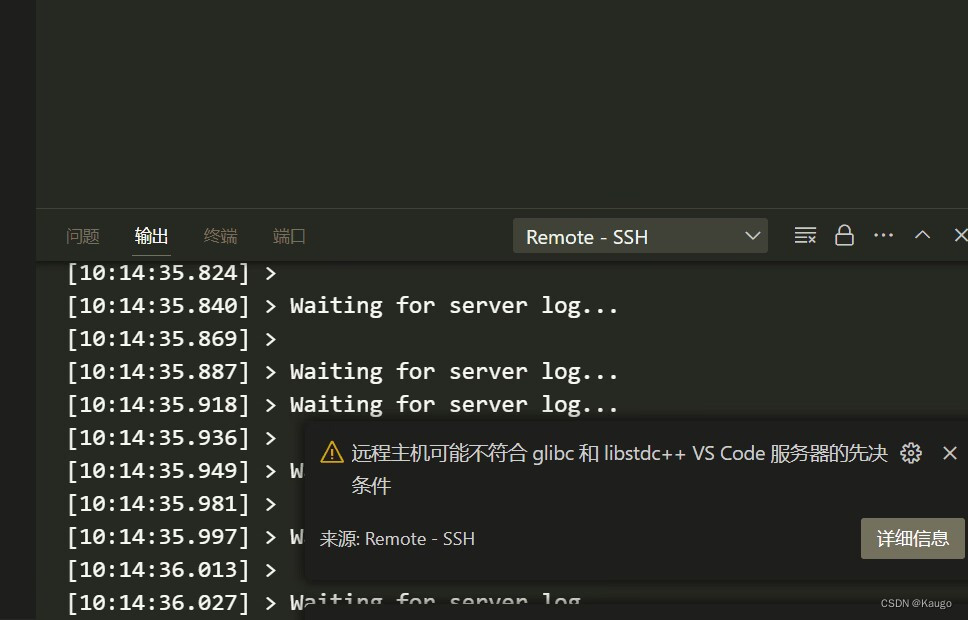
网上的方法我都试了一遍，内存也没满好好的，都不能用最后选择把VScode装回1.85版本，瞬间就能用了。

Linux下一切皆文件，指令的本质就是可执行文件，直接安装到了系统的某种路径下1.目录的可执行权限是表示你可否在目录下执行命令。2.如果目录没有-x权限，则无法对目录执行任何命令，甚至无法cd进入目即使目录仍然有-r读权限（这个地方很容易犯错，认为有读权限就可以进入目录读取目录下的文件）3.而如果目录具有-x权限，但没有-r权限，则用户可以执行命令，可以cd进入目录。但由于没有目录的读权限，所以在

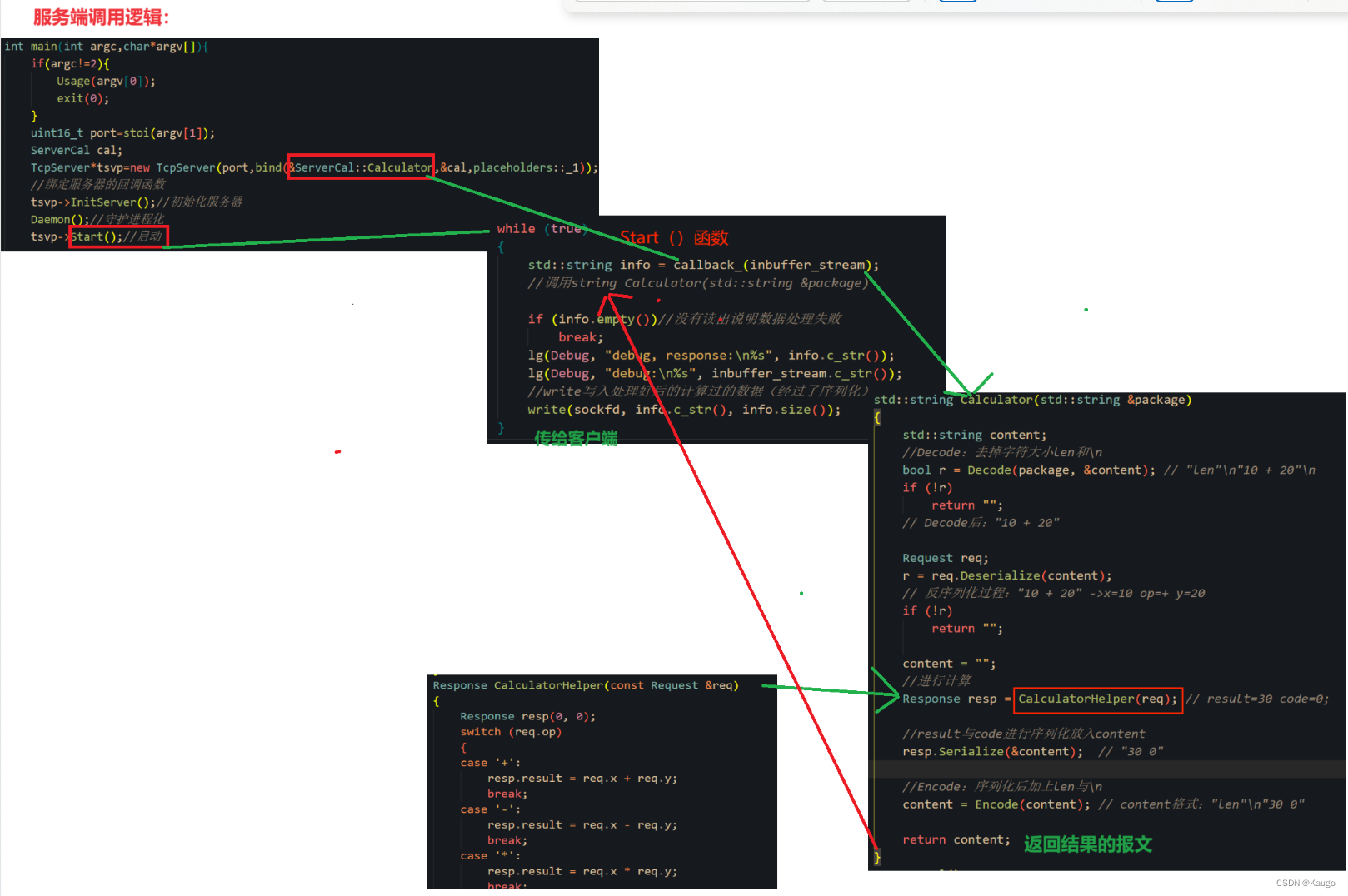
我们需要实现一个服务器版的加法器. 我们需要客户端把要计算的两个加数发过去, 然后由服务器进行计算, 最后再把结果返回给客户端`//编码：给序列化后的字符串加上字符长度与\n//目的：截取字符串“x op y”放入content中，并把与此字符串//相关的数据从总报文package中移除//len_str:len的字符串形式//// earse 移除报文 package.erase(0, tota

线程池:一种线程使用模式。线程过多会带来调度开销，进而影响缓存局部性和整体性能。而线程池维护着多个线程，等待着监督管理者分配可并发执行的任务。这避免了在处理短时间任务时创建与销毁线程的代价。线程池不仅能够保证内核的充分利用，还能防止过分调度。可用线程数量应该取决于可用的并发处理器、处理器内核、内存、网络sockets等的数量。线程池的应用场景：需要大量的线程来完成任务，且完成任务的时间比较短。WE