Android是一个广泛使用的开源操作系统，主要应用于移动设备，如智能手机、平板电脑、智能电视、智能手表等。它由Google主导开发，并构建。Android的开源特性、可定制性和丰富的生态系统，使其成为全球范围内最流行的操作系统之一。

这篇文章简要的概括了在网页开发过程中的关键步骤和技术要点，包括安装基础软件、设计网站外观、处理文件、HTML、CSS、JavaScript基础知识、发布网站以及万维网工作原理等内容。

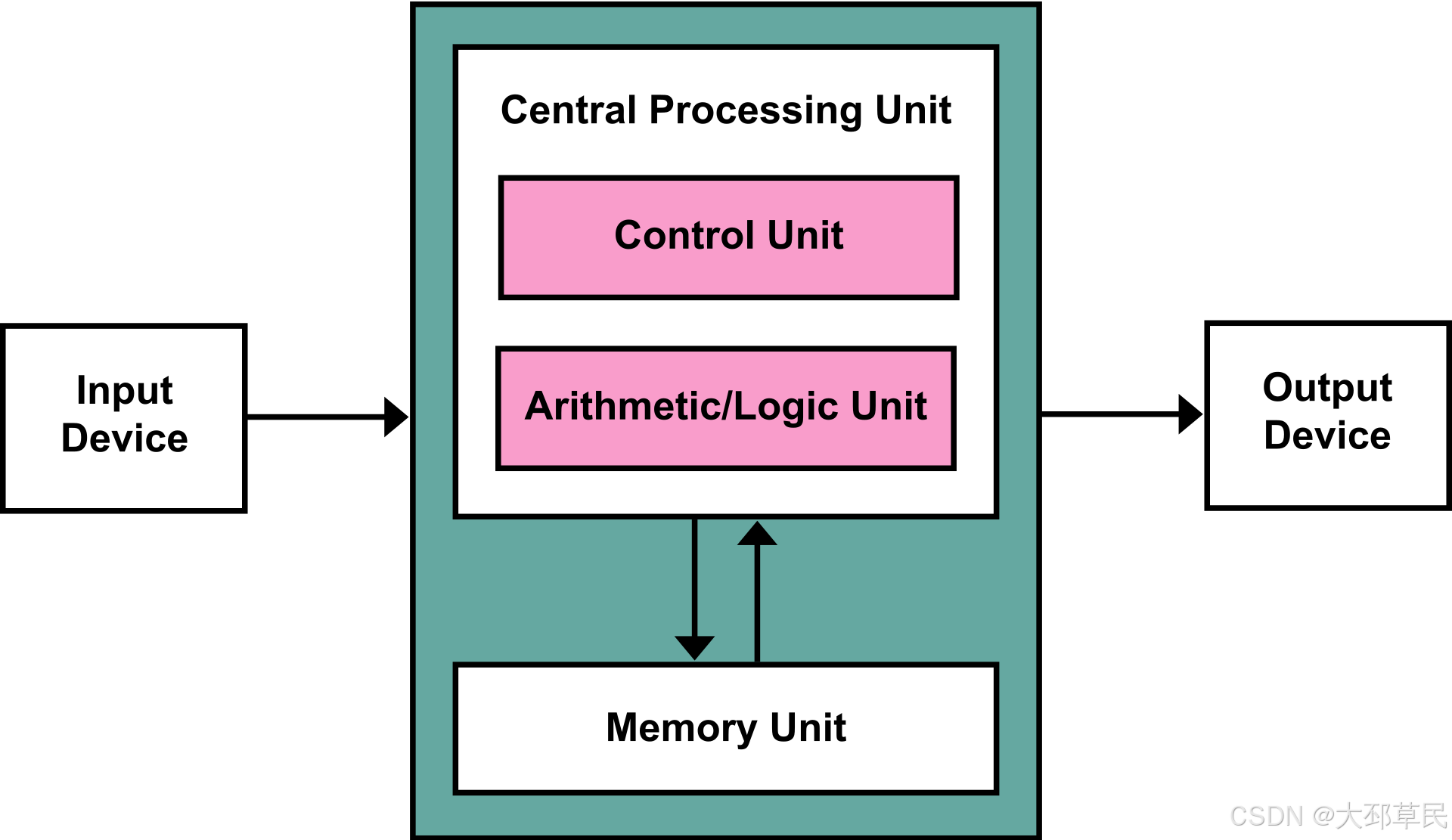
冯诺依曼架构和哈佛架构代表了计算机体系结构的两种基本设计理念。冯诺依曼架构由于其简洁性和灵活性，广泛应用于通用计算机中，而哈佛架构则通过分离程序存储和数据存储，在实时计算和数据处理要求较高的领域（如嵌入式系统、数字信号处理器等）表现出更高的性能。冯诺依曼架构的冯诺依曼瓶颈限制了其在某些高性能应用中的应用，而哈佛架构通过并行数据访问和指令访问，避免了这一瓶颈。在现代计算机系统中，虽然冯诺依曼架构仍占

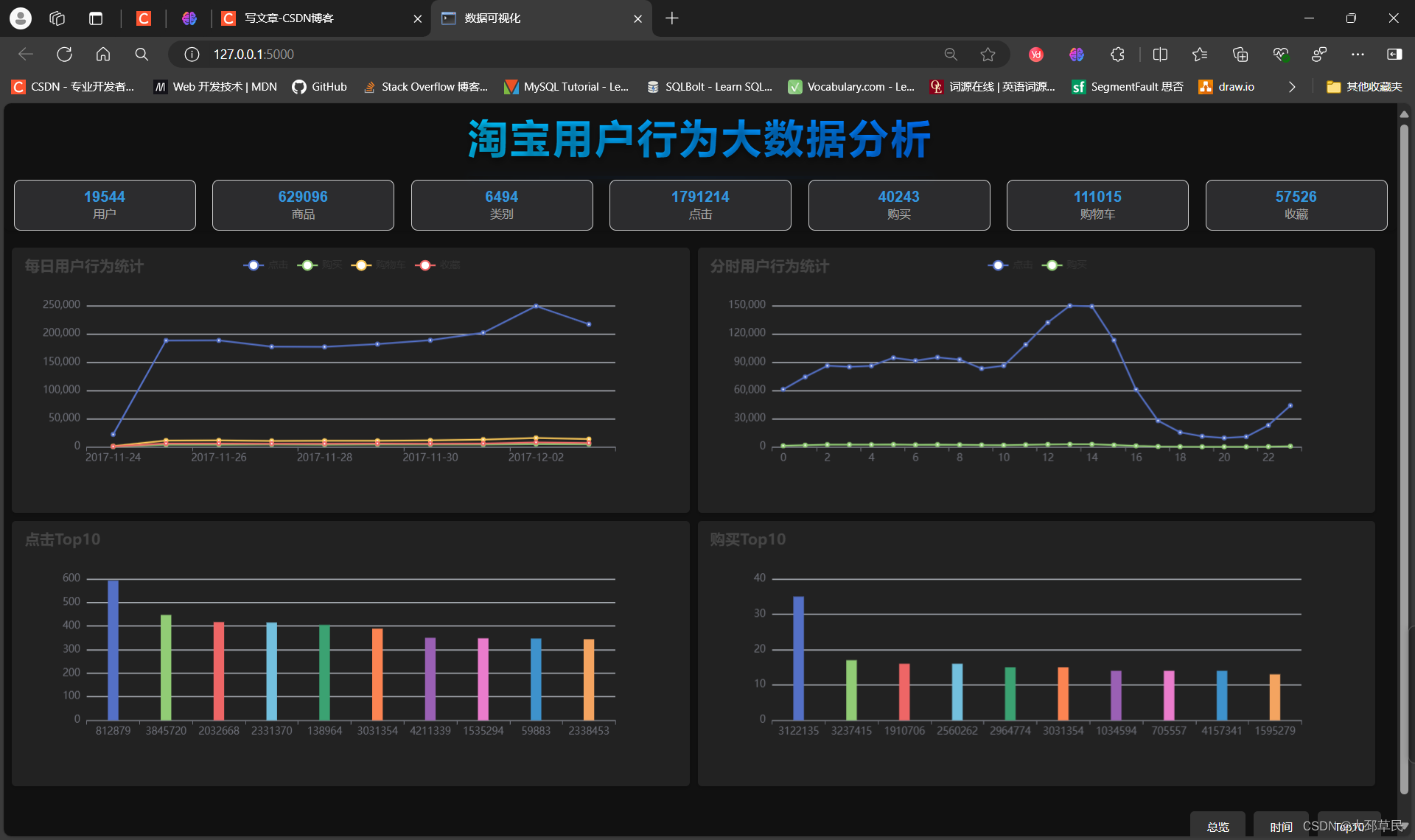
此项目旨在分析淘宝用户的行为数据，通过可视化技术展示关键统计数据，帮助了解用户的行为模式和偏好。项目包括数据处理、数据可视化以及后端数据服务。本项目通过对淘宝用户行为数据的分析与可视化，实现了用户行为模式的展示。项目使用了 Flask 作为后端框架，提供数据接口；使用 ECharts 进行前端数据可视化。通过数据处理和可视化，项目能够帮助用户了解淘宝用户的行为趋势和偏好，为进一步的分析和业务决策提

矩阵的性质是线性代数中的核心内容，理解这些性质有助于深入掌握矩阵的应用与运算。 掌握矩阵的加法与乘法性质、单位矩阵与零矩阵的作用、转置、逆矩阵、行列式、秩等基本性质，不仅能简化计算过程，还能为更复杂的数学问题提供解决思路，是学习和应用矩阵的基础。 1. 加法和乘法的交换性与结合性 矩阵加法的交换性 矩阵加法满足交换律，即： A + B = B + A A + B = B + A A+B=B+A 其

在求解一阶线性微分方程时，积分因子（Integrating Factor）是一个非常重要的工具，它能够将复杂的微分方程转化为一个可以直接积分的形式。通过使用积分因子，我们可以简化微分方程的结构，使得求解过程更加直接和有效。 1. 一阶线性微分方程的标准形式 首先，回顾一下 一阶线性微分方程 的标准形式，它通常写作： d y d x + P ( x ) y = Q ( x ) \frac{dy}{d

矩阵的行变换和列变换在矩阵的分析、简化及运算中扮演着非常重要的角色。这些变换可以用来简化矩阵结构，帮助我们在计算矩阵的逆、秩、解线性方程组以及理解矩阵的行空间和列空间时更加高效和直观。 1. 行变换的意义与应用 行变换（row transformations）是指对矩阵的行进行操作，主要包括以下三类操作： 行交换（Row swapping）：交换矩阵的两行。行倍乘（Row scaling）：将某一

在Excel中，单元格引用有三种主要类型：相对定位、绝对定位和混合定位。这些类型主要用于公式和函数中，决定在复制或拖动公式时引用如何变化。

Java编程中常用的获取数据长度的方式有三种： length 属性适用于数组， length() 方法适用于字符串， size() 方法适用于集合。

这些快捷键涵盖了Windows系统中的大部分常见操作，从窗口管理、文件操作到浏览器使用、截图、辅助功能等，掌握这些快捷键能够帮助开发者提高效率，节省大量时间。