动态规划（dynamic programming）能够高效解决一些经典问题，例如背包问题和最短路径规划。动态规划的基本思想是将待求解问题分解成若干个子问题，先求解子问题，然后从这些子问题的解得到目标问题的解。动态规划会保存已解决的子问题的答案，在求解目标问题的过程中，需要这些子问题答案时就可以直接利用，避免重复计算。

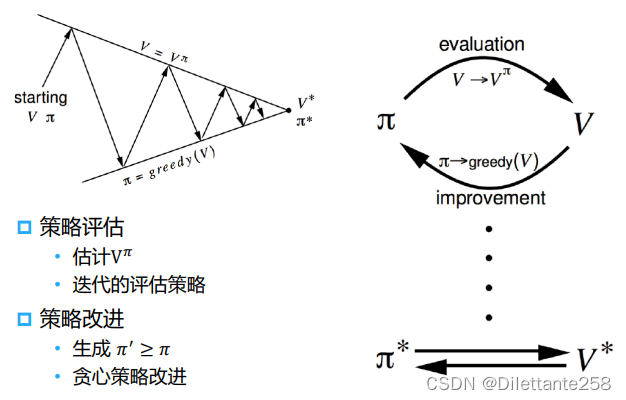
马尔可夫决策过程（Markov decision process，MDP）是强化学习的重要概念。强化学习中的环境一般就是一个马尔可夫决策过程。与多臂老虎机问题不同，马尔可夫决策过程包含状态信息以及状态之间的转移机制。

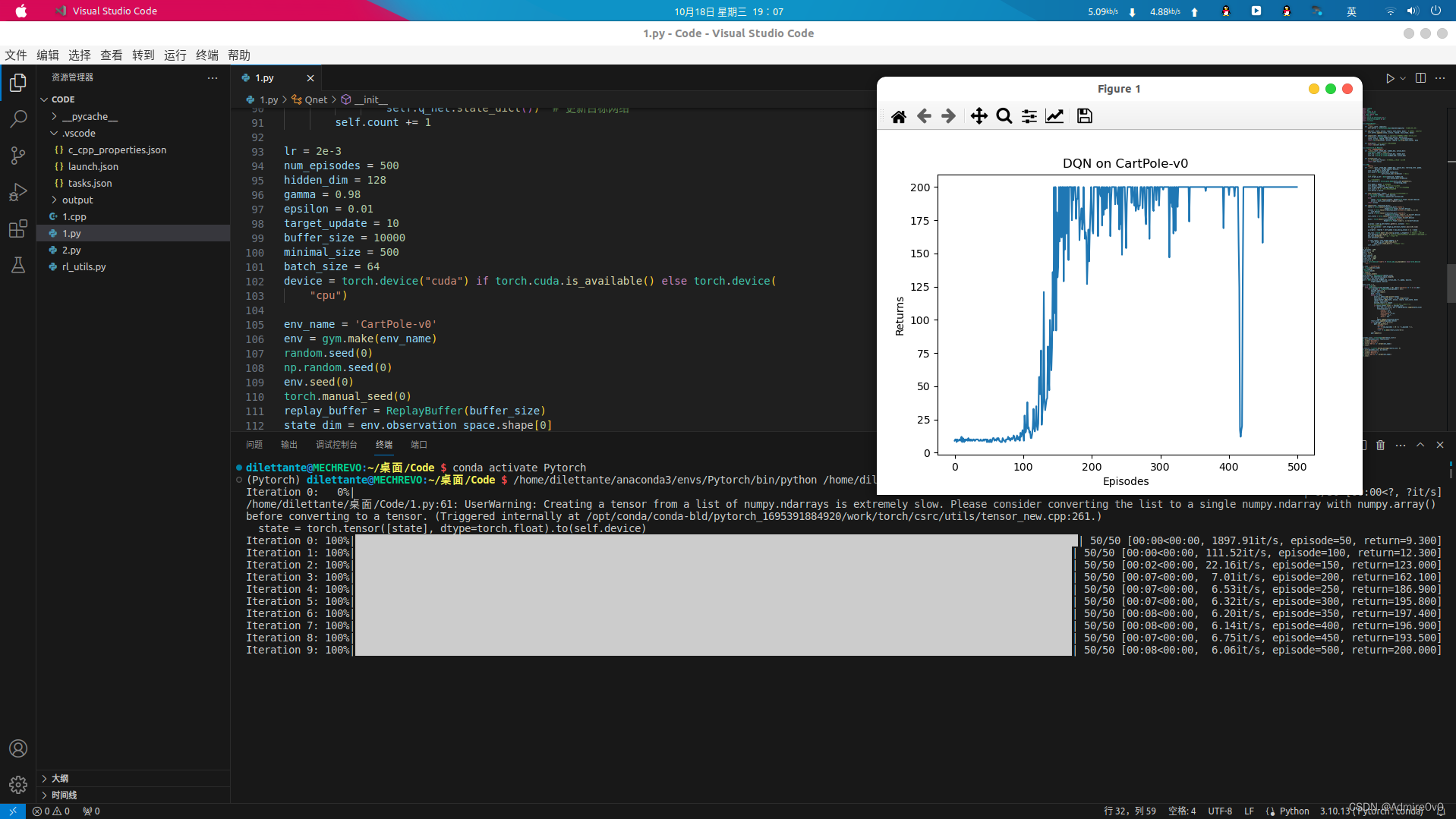
入门机器学习的第一只拦路虎就是配置环境，一些经典教材和教程的上的那些代码都是在几年前写作的，然后呢，这些过时的代码也就相应需要配置那些环境。本文在Ubuntu 20.04 LTS环境下安装并配置了gym 0.19.0环境，使得一些函数如env.seed()得以使用。

南京邮电大学 离散数学 23年第一学期考试回忆。20分填空题+80分大题用的是橙色封面的《离散数学》。

南京邮电大学 数学实验A 实验报告 23-24-2学期。留档使用

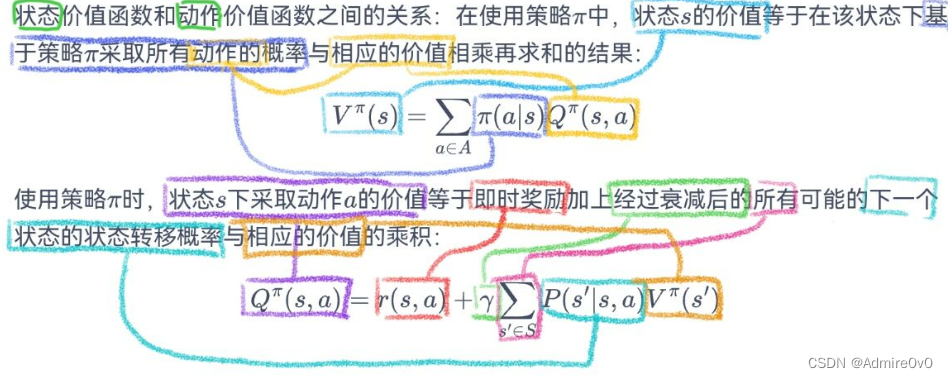
书接上一节动态规划算法适用于已知马尔可夫决策过程的情况，可以直接解出最优价值或策略。但在大部分情况下，马尔可夫决策过程的状态转移概率是未知的，这时就需要使用无模型的强化学习算法。无模型的强化学习算法不需要事先知道环境的奖励函数和状态转移函数，而是通过与环境交互采样数据来学习。模型无关的强化学习直接从经验中学习值（value）和策略 （policy），而无需构建马尔可夫决策过程模型（MDP）。关键步

设生产速率为常数 k，销售速率为常数 r，k>r，在每个生产周期T内，开始的一段时间(为了建模方便，假设生产量和销售量的变化都是连续的，生产周期T可以不是整数。)只销售不生产，画出存贮量 q(t) 的图形。停止生产后，库存数逐渐减少，直至库存数变为0，此时一个周期结束。，以平均每天总费用最小为目标确定最优生产周期。所以，这段周期内的总费用为：总存储费用+生产准备费。对(4)式除以周期T，求平均每天

南京邮电大学 算法设计与分析 课后习题

设生产速率为常数 k，销售速率为常数 r，k>r，在每个生产周期T内，开始的一段时间(为了建模方便，假设生产量和销售量的变化都是连续的，生产周期T可以不是整数。)只销售不生产，画出存贮量 q(t) 的图形。停止生产后，库存数逐渐减少，直至库存数变为0，此时一个周期结束。，以平均每天总费用最小为目标确定最优生产周期。所以，这段周期内的总费用为：总存储费用+生产准备费。对(4)式除以周期T，求平均每天