定义编码器self.embedding = nn.Embedding(vocab_size, ebd_size, padding_idx=3) # 将token表示为embedding# encoder_inputs从(batch_size, seq_len)变成(batch_size, seq_len, emb_size)再调整为(seq_len, batch_size, emb_size)

batch_first 为 True时output的tensor为（batch,seq,feature）,否则为（seq,batch,feature）# 初始化隐藏状态和细胞状态# 计算输出和最终隐藏状态# 网络结构。

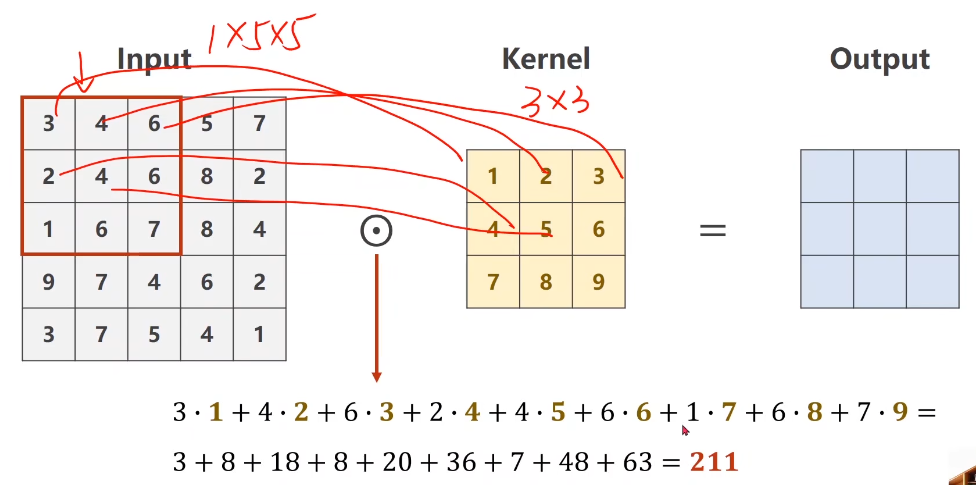
每一个通道的像素值与对应的卷积核通道的数值进行卷积，因此每一个通道会对应一个输出卷积结果，三个卷积结果对应位置累加求和，得到最终的卷积结果（这里卷积输出结果通道只有1个，因为卷积核只有1个。因此整个卷积层的尺寸为（m*n*k1*k2）是一个4维张量，其中m表示卷积核的数量，n表示通道数量，k1表示每一个卷积核通道的宽，k2表示每一个卷积核通道的高。假设卷积核只有1个，卷积核通道为3，每个通道的卷积

本篇论文发表于ACL-2022原文链接源码模态：图像+文本基于多模态方面的情感分析(MABSA)近年来越来越受到关注。然而，以前的方法要么(i)单独使用预训练的视觉和文本模型，忽略了跨模态的对齐;要么(ii)使用预训练的视觉语言模型，这些模型带有一般的预训练任务，这不足以识别细粒度的方面、观点及其跨模态的对齐。本文提出了一个针对MABSA的任务特定的视觉语言预训练框架(VLPMABSA)，这是一个

每一个通道的像素值与对应的卷积核通道的数值进行卷积，因此每一个通道会对应一个输出卷积结果，三个卷积结果对应位置累加求和，得到最终的卷积结果（这里卷积输出结果通道只有1个，因为卷积核只有1个。因此整个卷积层的尺寸为（m*n*k1*k2）是一个4维张量，其中m表示卷积核的数量，n表示通道数量，k1表示每一个卷积核通道的宽，k2表示每一个卷积核通道的高。假设卷积核只有1个，卷积核通道为3，每个通道的卷积

每一个通道的像素值与对应的卷积核通道的数值进行卷积，因此每一个通道会对应一个输出卷积结果，三个卷积结果对应位置累加求和，得到最终的卷积结果（这里卷积输出结果通道只有1个，因为卷积核只有1个。因此整个卷积层的尺寸为（m*n*k1*k2）是一个4维张量，其中m表示卷积核的数量，n表示通道数量，k1表示每一个卷积核通道的宽，k2表示每一个卷积核通道的高。假设卷积核只有1个，卷积核通道为3，每个通道的卷积

Universal Approximation Theorem：一个具有足够多的隐藏节点的多层前馈神经网络，可以逼近任意连续的函数。w 是仿射变换和偏置 b ，通常情况下我们只考虑对参数 w 作惩罚，这是由于在拟合偏置 b 时所需数据量比较少就可以拟合的很好了。通过在损失函数中加入对模型参数权值矩阵中各元素绝对值之和的惩罚项，来限制模型参数的值。每层每个神经元，以p 的概率保留，以1-p 的概率将

batch_first 为 True时output的tensor为（batch,seq,feature）,否则为（seq,batch,feature）# 初始化隐藏状态和细胞状态# 计算输出和最终隐藏状态# 网络结构。

/*前边两个为一种做法*//*后边有另外的做法（差分方程以及利用矩阵去做）*/第一种做法这是王道数据结构考研复习指导的第一章思维拓展的题目。关于斐波那契数列的简介：　　斐波那契数列，又称黄金分割数列，指的是这样一个数列：0、1、1、2、3、5、8、13、21、34、……在数学上，斐波纳契数列以如下被以递归的方法定义：F（0）=0，F（1）=1，F（n）=F(n-1)+F(n-2)（n≥2，n∈N*

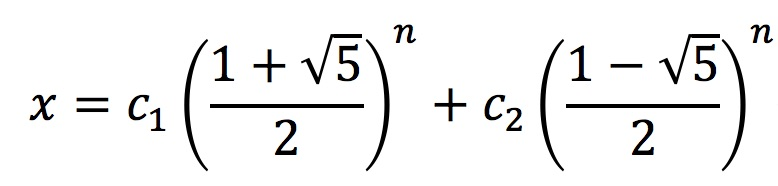
从映射分析：存在反函数的函数，定义域到值域是1-1对应或者叫双射。定义域和值域分别为D,B，若对于x1，x2∈D，x1≠x2,推出f(x1)≠f(x2),f(x1),f(x2)∈B。那么就叫做1-1对应或双射。【注意，这里的集合已经压缩到定义域和值域了，满射就能保证了】。这样的映射关系，存在一个逆映射，即存在反函数。（1）单调性到反函数若函数是单调的，无论是增还是减，都能保证x1，x2∈D，x1≠