路径规划算法中的OBVP例子文章目录路径规划算法中的OBVP例子1.已知量1.1 目标函数1.2 变量1.3 状态方程1.4 初始值2.固定边界条件2.1 构建系统的Hamiltonian矩阵HHH和协变量λ\lambdaλ2.2 通过Hamiltonian矩阵对协变量进行求导2.3 最小化输入变量2.4 通过积分求得最优轨迹s∗s^*s∗2.5 最终状态确定最优轨迹的参数2.6 最优状态下目标函

Minimum Snap 轨迹优化问题文章目录Minimum Snap 轨迹优化问题1. 前景2. 基本原理2.1 轨迹生成条件2.2 评价函数2.3 约束条件2.3.1 导数约束(Derivative constraint)2.3.2 连续性约束(Continuity constraint)2.4 问题求解附录1. 凸函数基本概念2. QP问题1. 前景上一章介绍了OBVP的基本原理，但OBVP

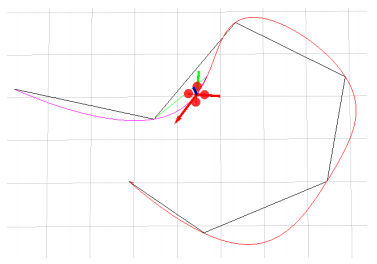
C++结合OpenCV实现RRT算法文章目录C++结合OpenCV实现RRT算法1.RRT算法简介2.算法整体框架流程2.1 rand点的建立2.2 near和new点的建立2.3 安全性检查2.4 算法结束判断3.RRT代码框架3.1 主函数3.2 地图数据的获取3.3 RRT算法的实现3.3.1 起点入树3.3.2 rand点的获取3.3.3 near点的获取3.3.4 new点的获取3.3.

G2O使用说明（SLAM）范例：在使用G2O要明确目标函数是什么，优化变量是几维，误差项是几维。举例说明：现在有很多个点符合y=exp(ax2+bx+c)+wy=exp(ax^{2}+bx+c)+wy=exp(ax2+bx+c)+w,其中w为高斯噪声。那么目标函数就是e(a,b,c)=y−exp(ax2+bx+c)e(a,b,c)=y-exp(ax^{2}+bx+c)e(a,b,c)=y−exp(

三维点云课程—Harris特征点介绍三维点云课程---Harris特征点介绍三维点云课程---Harris特征点介绍1.图片的Harris特征值介绍2.点云中的Harris特征值介绍2.1 Harris3D With Intensity2.2 Harris3D Without Intensity2.3 扩展 Harris 6D3.总结在讲解三维的HarrisHarrisHarris之前，先来介绍一

三维点云课程—RANSAC结合最小二乘求解点云的地面三维点云课程---RANSAC结合最小二乘求解点云的地面三维点云课程---RANSAC结合最小二乘求解点云的地面1.RANSAC的步骤2.RANCAC的代码分析2.1输入参数τ，N\tau，Nτ，N的分析2.2 平面模型的创建2.3统计内点的个数2.4最小二乘优化2.5提前终止RANSAC的迭代3.RANSAC完整代码**原始数据**![在这里插

三维点云课程—ICP(Point-to-Point)三维点云课程---ICPPoint-to-Point三维点云课程---ICP(Point-to-Point)1.ICP问题描述2.ICP问题分析3.ICP证明3.11N1T(B−RA)T(B−RA)1\frac{1}{N}1^T(B-RA)^T(B-RA)1N1​1T(B−RA)T(B−RA)1的化简3.2 2tr((B−RA)11N1T(B−R

路径规划算法中的OBVP原理介绍文章目录路径规划算法中的OBVP原理介绍1. 前景介绍2. 原理介绍3. 案例说明3.1 已知量3.2 求解3.3 边界问题扩展附录1.Pontrayagin's 最小值原理2. 多项式求根1. 前景介绍例如一个5次多项式表示两点间的轨迹方程x(t)=c5t5+c4t4+c3t3+c2t2+c1t1+c0x(t)=c_5t^5+c_4t^4+c_3t^3+c_2t^

基于Kinodynamic的路径规划简单介绍文章目录基于Kinodynamic的路径规划简单介绍1. 机器人模型1.1 Unicycle Model1.2 Differential Drive Model1.3 Car Model2. State Lattice Planning2.1 控制空间采样2.2 状态空间采样Kinodynamic=Kinematic+Dynamic，其中Kinemati

三维点云课程—ICP (Point-to-Plane)由于Point-to-Point的方法不允许平面之间的滑动，故提出了Point-to-Plane的ICP方法1.Point-to-Plane的原理介绍Point-to-Plane不同于Point-to-Point的方法，它是求源点云中的点pip_ipi​ 到目标点云中qiq_iqi​组成的曲面的距离。也就是说，此时点云需要提供每个点的法向量。数