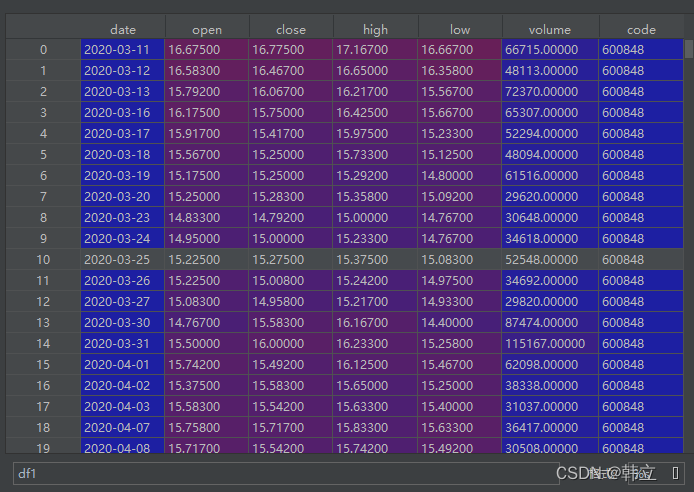
输入timeColSer销售时间这一列，Series数据类型，例‘2018-01-01星期五’输出分割后的时间，返回Series数据类型，例‘2018-01-01’统计月均消费次数（同一天一个人的所有消费算作一次消费）转换日期过程中不符合日期格式的数值会被转换为空值。其中，商品编码就是商品名称这两列数据重复。将'销售数量'这一列小于0的数据排除掉。以下可知购药时间和社保卡号存在缺失值。定义函数分割

4：假如从2010 1.1 开始， 每月第一个交易日买入一手股票，每年最后一个交易日卖出所有股票， 到今天为止，我们受益如何？4：假如从2010 1.1 开始， 每月第一个交易日买入一手股票，每年最后一个交易日卖出所有股票， 到今天为止，我们受益如何？其次，读取k线数据，并保存下来，然后重新读取并完成目标2。3：输出该股票所有开盘比前日收盘跌幅超过2%的日期。3：输出该股票所有开盘比前日收盘跌幅超

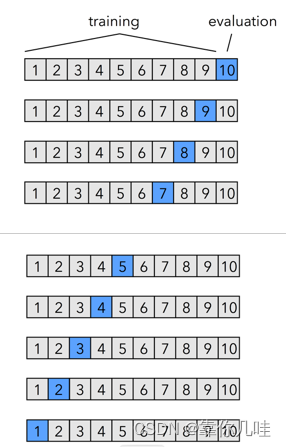
简单交叉验证方法：将原始数据集随机划分成训练集和验证集两部分。比如，将样本按照70%~30%的比例分成两部分，70%的样本用于训练模型；30%的样本用于模型验证。缺点：（1）数据都只被所用了一次，没有被充分利用（2）在验证集上计算出来的最后的评估指标与原始分组有很大关系。代码k折交叉验证 为了解决简单交叉验证的不足，提出k-fold交叉验证。1、首先，将全部样本训练集划分成k个大小相等的样本子集；

基尼指数和信息熵都是用来描述系统混乱度的量数学形式不一样，干的事是一样的不纯度（impurity）--GINI系数：（不纯度就是混乱度）公式 例子（与信息熵干的是一件事） 决策树模型理解二、决策树的学习（训练）过程一棵决策树的生成过程主要分为以下3个部分:特征选择：特征选择是指从训练数据中众多的特征中选择一个特征作为当前节点的分裂标准，如何选择特征有着很多不同量化评估标准标准，从而衍生出不同的决策

4：假如从2010 1.1 开始， 每月第一个交易日买入一手股票，每年最后一个交易日卖出所有股票， 到今天为止，我们受益如何？4：假如从2010 1.1 开始， 每月第一个交易日买入一手股票，每年最后一个交易日卖出所有股票， 到今天为止，我们受益如何？其次，读取k线数据，并保存下来，然后重新读取并完成目标2。3：输出该股票所有开盘比前日收盘跌幅超过2%的日期。3：输出该股票所有开盘比前日收盘跌幅超

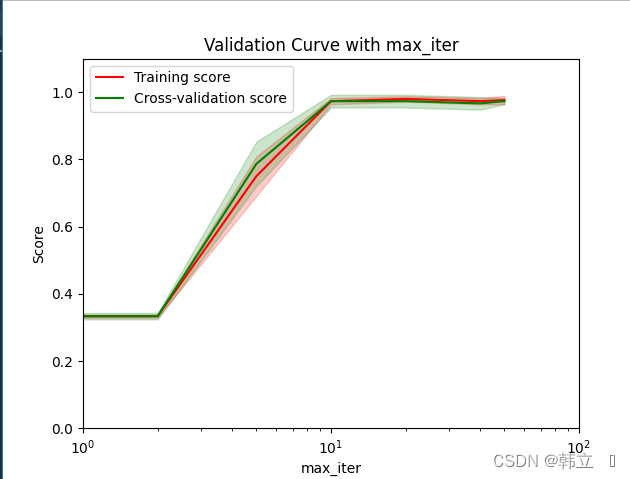
需要注意的是如果我们使用验证分数来优化超参数，那么该验证分数是有偏差的，它无法再代表模型的泛化能力，我们就需要使用其他测试集来重新评估模型的泛化能力。验证曲线和学习曲线的区别是，横轴为某个超参数的一系列值，由此来看不同参数设置下模型的准确率(评价标准)，而不是不同训练集大小下的准确率。从验证曲线上可以看到随着超参数设置的改变，模型可能从欠拟合到合适再到过拟合的过程，进而选择一个合适的设置，来提高模

输入timeColSer销售时间这一列，Series数据类型，例‘2018-01-01星期五’输出分割后的时间，返回Series数据类型，例‘2018-01-01’统计月均消费次数（同一天一个人的所有消费算作一次消费）转换日期过程中不符合日期格式的数值会被转换为空值。其中，商品编码就是商品名称这两列数据重复。将'销售数量'这一列小于0的数据排除掉。以下可知购药时间和社保卡号存在缺失值。定义函数分割

简单交叉验证方法：将原始数据集随机划分成训练集和验证集两部分。比如，将样本按照70%~30%的比例分成两部分，70%的样本用于训练模型；30%的样本用于模型验证。缺点：（1）数据都只被所用了一次，没有被充分利用（2）在验证集上计算出来的最后的评估指标与原始分组有很大关系。代码k折交叉验证 为了解决简单交叉验证的不足，提出k-fold交叉验证。1、首先，将全部样本训练集划分成k个大小相等的样本子集；

一次定时器中断溢出的时间可以由以下的公式计算得来：一、TIM（Timer）定时器基本定时器中断可以对输入的时钟进行计数，并在计数值达到设定值（自动重装值）时触发中断；16位计数器、预分频器、自动重装寄存器的时基单元，在72MHz计数时钟下可以实现最大59.65s的定时；不仅具备基本的定时中断功能，而且还包含内外时钟源选择、输入捕获、输出比较、编码器接口、主从触发模式等多种功能；根据复杂度和应用场景

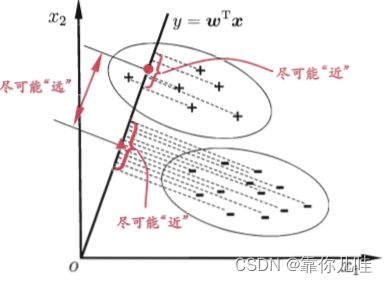
线性判别分析（Linear Discriminant Analysis，简称LDA）是一种经典的监督学习的数据降维方法，也叫做Fisher线性判别（Fisher Linear Discriminant，FLD），是模式识别的经典算法 ，它是在1996年由Belhumeur引入模式识别和人工智能领域的。LDA的主要思想是将一个高维空间中的数据投影到一个较低维的空间中，且投影后要保证各个类别的类内方差