## Sysfs实现GPIO中断事件监听摘要本文提供基于Linux sysfs接口的GPIO中断事件完整C语言解决方案。通过操作`/sys/class/gpio`系统文件，实现GPIO引脚导出、方向配置（输入模式）和中断边沿设置（支持rising/falling/both三种触发模式）。核心采用poll()系统调用监控value文件的POLLPRI事件，实时检测引脚电平变化并区分上升沿/下降沿事件

本文介绍了在WSL2环境下自动化检查并启动TFTP服务的解决方案脚本，适用于PetaLinux嵌入式开发。该解决方案通过三重检测机制(进程检查、端口监听、服务状态)，自动识别用户权限并选择合适的启动方式，提供清晰的状态提示。通过将其集成到PetaLinux环境配置脚本中，实现了开发时TFTP服务的自动可用性保障，避免了手动启动服务的繁琐过程。文章详细说明了了脚本实现、集成方法、配置优化建议和使用效

本文介绍了LVGL数据可视化中图表控件的应用。通过数学模型将数据点映射为屏幕坐标，详细展示了实时监控图表的创建过程。内容包括：1）图表的基本数学模型，通过公式将数据转换为屏幕坐标；2）实战演示如何创建多系列实时数据图表，包括图表配置、数据系列添加和图例创建；3）代码示例展示了温度、湿度、压力三组数据的可视化实现，以及定时更新机制。该方案适用于嵌入式系统的GUI开发，能够有效呈现传感器数据变化趋势。

LVGL是一个开源的嵌入式图形库，专为资源受限设备设计，能在低内存和低速CPU下提供流畅的UI体验。它具有40+控件、类似CSS的样式系统、高级图形功能和高度可移植性，最低仅需64kB Flash和16kB RAM。LVGL采用事件驱动架构，通过周期性中断和主循环处理动画、输入和重绘。本文通过VS Code+PlatformIO环境，演示了如何在PC模拟器上创建LVGL的"Hello W

本文以Motorcomm YT8531SH PHY芯片为例，深入解析Linux网络PHY驱动的架构与实现。Linux网络采用分层设计，包含MAC驱动、PHY驱动和MDIO总线。PHY驱动通过phy_driver结构体实现，包含设备探测、初始化配置、电源管理等关键回调函数。驱动加载流程包括MDIO总线初始化、PHY驱动注册、硬件探测匹配等阶段。设备树配置涵盖时钟输出、RGMII时序调整、驱动强度等关

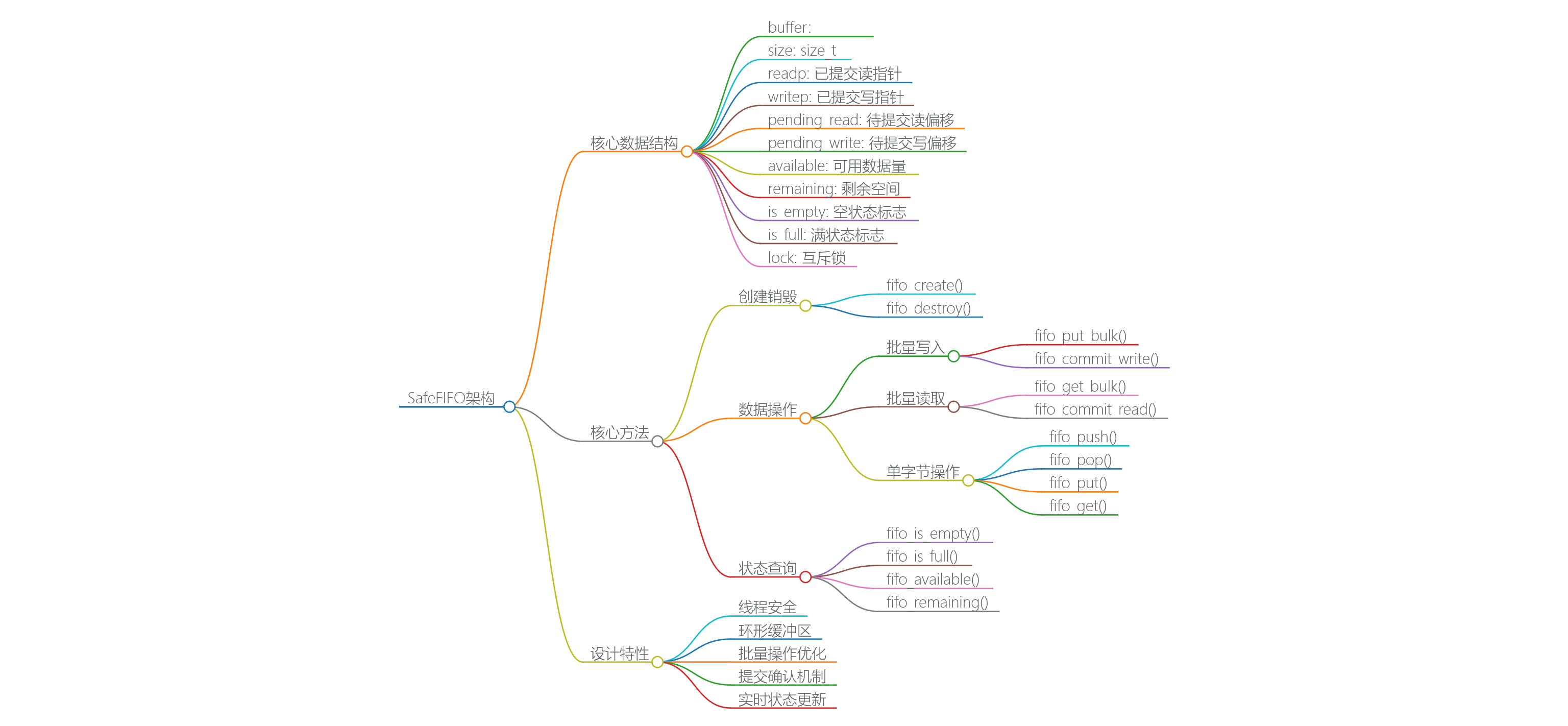
通过本文的详细解析，读者可以全面理解这个线程安全FIFO队列的实现细节，掌握其设计精髓，并能够根据实际需求进行扩展优化。该实现展示了良好的跨平台设计思想和线程安全实践，是学习并发数据结构的优秀范例。所提供的代码在Ubuntu20.04和win10中都验证通过，并可方便移植到RTOS以及裸机嵌入式中使用。可以作为一些简单通信系统的基础服务模块

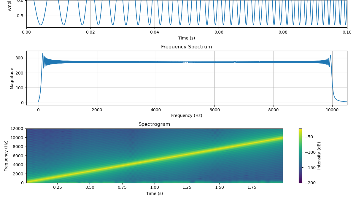
本文介绍了如何使用C语言生成调频Chirp信号并用Python验证其正确性。Chirp信号是一种频率随时间线性变化的信号，文中给出了其数学表达式和关键参数说明。C语言实现部分通过结构体配置参数，计算瞬时频率并生成信号数据，最终保存为二进制文件。Python验证通过读取二进制文件，绘制时域波形、频谱图和时频谱，验证信号频率变化的线性特征和参数一致性。结果显示，生成的Chirp信号符合预期，频率从10

设备树作为现代Linux系统中描述硬件配置的标准方式，已经广泛应用于ARM、PowerPC等架构。它通过将硬件描述与内核分离，提高了系统的可移植性和可维护性。掌握设备树的原理和应用，对于嵌入式Linux开发者和内核驱动开发者来说是一项必备技能。

本文深入解析了U-Boot环境变量在嵌入式系统启动过程中的关键作用，特别针对从QSPI Flash启动U-Boot后再从eMMC加载Linux系统的完整流程。文章首先通过实战案例展示了如何通过修改u-boot_env.txt实现EMMC启动，详细分析了bootcmd、default_bootcmd等核心环境变量的调用逻辑。重点解读了uenvboot变量的工作机制，该机制通过检测uEnv.txt文件

设计模式是软件开发中解决常见问题的可复用方案，主要分为三类：创建型（如工厂方法、单例）、结构型（如适配器、代理）和行为型（如观察者、策略）。本文详细介绍了各类模式的核心思想、UML图示、代码示例及适用场景，并探讨了其在现代框架（如Spring、React）中的应用。合理使用设计模式能提升代码可维护性与扩展性，但应避免过度设计。掌握这些模式有助于构建灵活、健壮的软件系统。