最小二乘法拟合直线的核心思想是：给定一组数据点（xi, yi），其中i=1, 2, …, N，我们希望找到一条直线y = kx + b，使得这些点到直线的垂直距离的平方和最小。这里的k是直线的斜率，b是直线的截距。

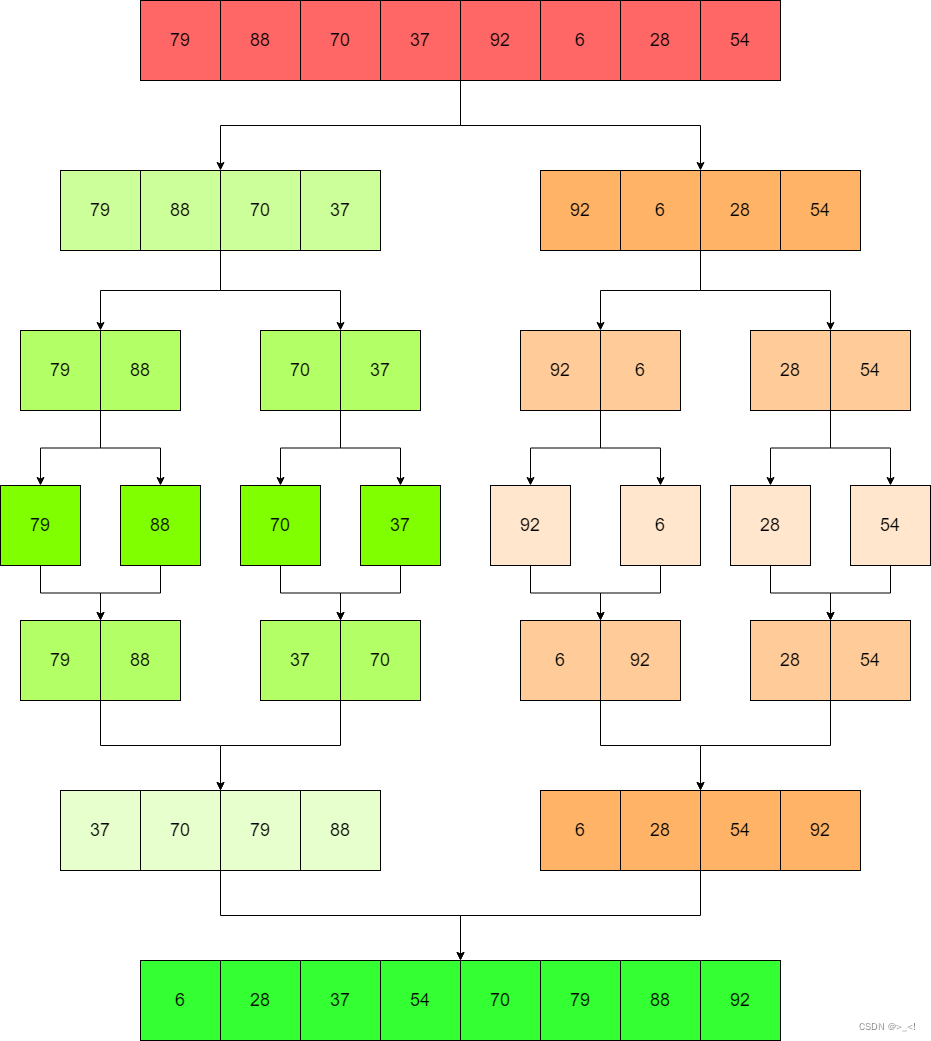
合并排序算法通过采用分治策略和递归思想，实现了高效、稳定的排序功能。本文将深入探讨合并排序算法的原理、实现步骤，并讨论其优缺点。

路径跟踪算法之模型预测控制(MPC)跟踪1.MPC简介模型预测控制（以下简称 MPC）是一种依赖于系统模型进行数学优化的复杂控制器。它利用优化算法计算有限时间范围内一系列的控制输入序列，并优化该序列，但控制器仅执行序列中的第一组控制输入，然后再次重复该循环。MPC 主要分为 3 个关键步骤：模型预测、滚动优化、反馈校正。2.MPC在轨迹跟踪过程中的应用在轨迹跟踪应用领域，通常 MPC 建模可根据机

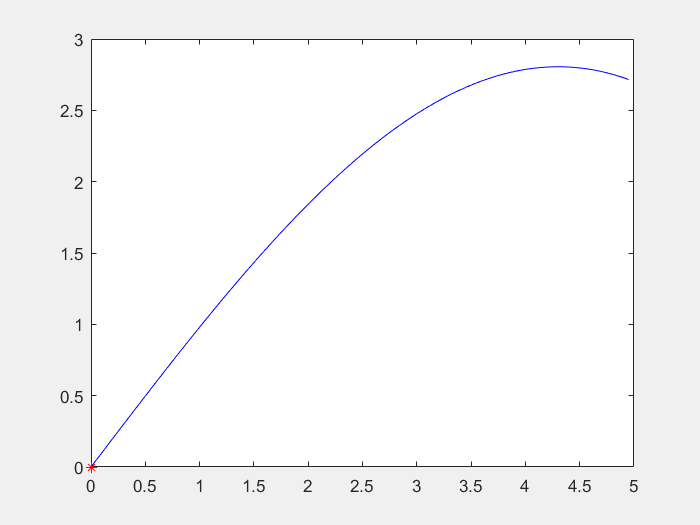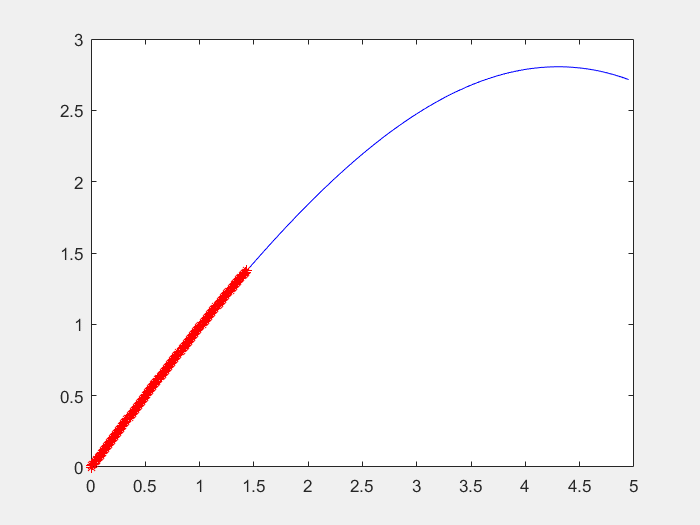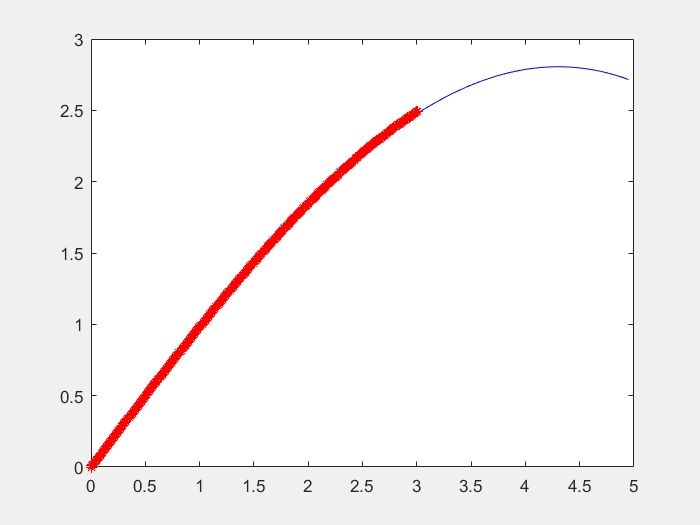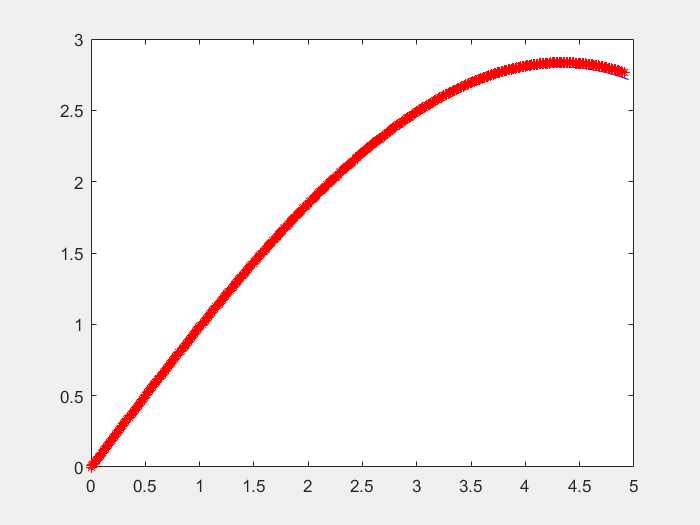
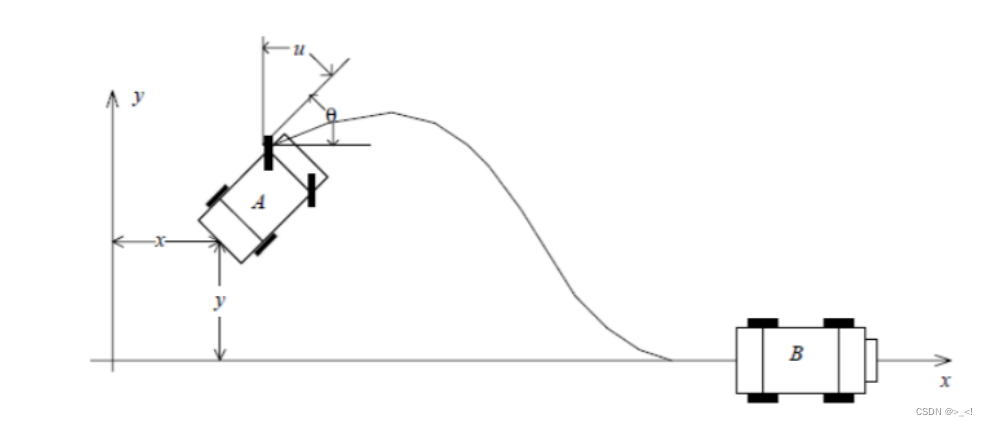
本文基于一个实例，阐述如何设计模糊控制器实现车辆路径跟踪。目标是设计一个控制器，在理想的车辆运动学数学模型的情况下，控制车辆沿着x轴方向前进，这便是一个典型的简化方向的路径跟踪问题。假设小车可以以v=0.5m/s的恒定速度向前移动。并且假设小车配备有陀螺仪等传感器，该传感器可以随时测量小车当前的位置（x，y）和方向（角度）。那么本跟踪问题的解决就是需要设计一个跟踪控制器，根据小车的实际位置，调整小

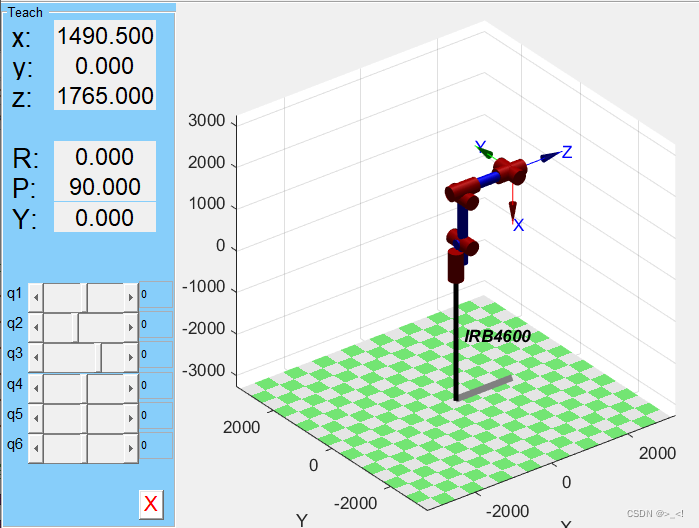
对于工业机械臂而言，运动学是不考虑力学特性的情况下对机械臂的几何参数与其位置、速度、加速度等运动特性的关系研究。DH建模是运动学的基础，全称为Denavit-Hartenberg建模方法，是一种广泛应用于机器人运动学中的建模技术。该方法通过在每个连杆上建立坐标系，并利用齐次坐标变换来实现连杆之间的坐标转换。通过依次变换，可以推导出末端执行器相对于基坐标系的位姿，从而建立机器人的运动学方程。以IRB

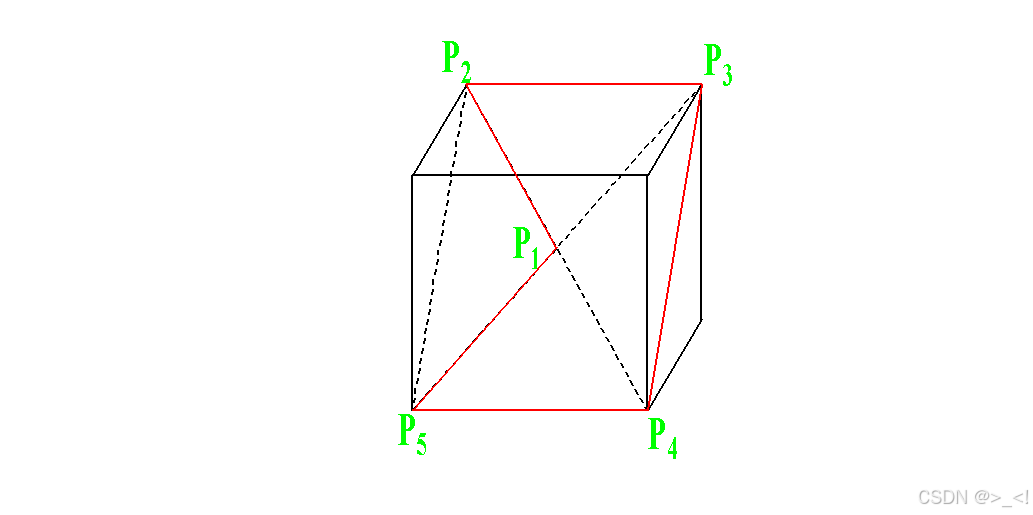
位置性能代表的是机器人在工作空间内运动点的特性，对于机器人在笛卡尔空间的运动，空间坐标系的原点代表机器人的指令位置，球状的点集群表示多个实际位置。那么，机器人的位置性能的评估主要包括：机器人的指令点位置和实际点位置的之间的相对关系评估；实际点位置之间的相互关系的评估。参考国标GB/T-12642，对位置准确度和重复性指标进行介绍。

TSP问题由于问题的可行解是所有顶点的全排列，随着顶点数的增加，会产生组合爆炸，它是一个NP完全问题。由于其在交通运输、电路板线路设计以及物流配送等领域内有着广泛的应用，国内外学者对其进行了大量的研究。早期的研究者使用精确算法求解该问题，常用的方法包括：分枝定界法、线性规划法、动态规划法等。但是，随着问题规模的增大，精确算法将变得无能为力，因此，在后来的研究中，国内外学者重点使用近似算法或启发式算

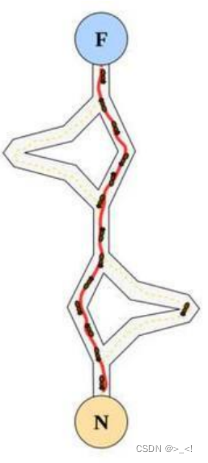
y+1=0的椭圆，参数ABCDEF未知待求。那么就可以通过matlab自带的非线性拟合函数nlinfit，带入离散的xy数据，反向求出ABCDEF这6个系数的值，这样，你就得到了最可以符合数据分布的一个椭圆方程。参数拟合，即假定已知了很多组x,y的坐标数据，并发现数据的分布规律和椭圆类似，我们先假设有一个方程表达式为A。计算出ABCDEF这6个系数的值后，椭圆的一般方程就确立了。这里已经将拟合出来

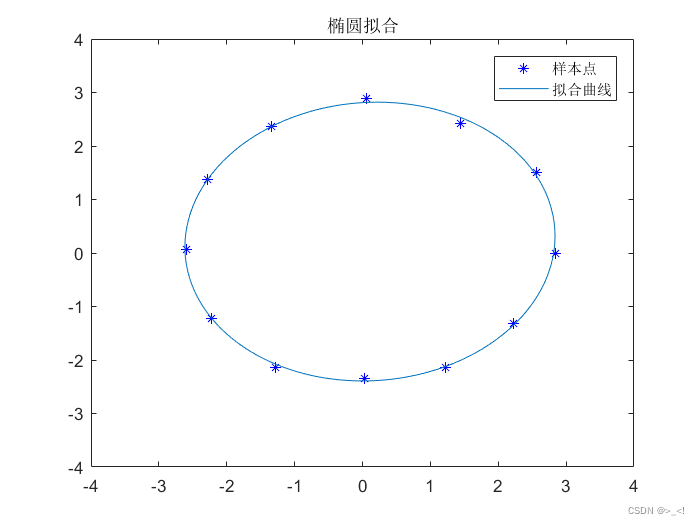
空间中一个坐标系相对于另一个坐标系的变换关系用新坐标系的三个坐标轴相对于原坐标系的方向矢量来确定，可用 矩阵来描述。用齐次矩阵（4x4）来统一描述刚体的位置和姿态：其中，R便是描述姿态的旋转矩阵。和沿着三个坐标轴的平移运动不一样，旋转矩阵显得很不直观，也繁琐。因此往往需要使用更简洁的方式来描述姿态变换。固定角与欧拉角便是最常规的两种。

本文基于一个实例，阐述如何设计模糊控制器实现车辆路径跟踪。目标是设计一个控制器，在理想的车辆运动学数学模型的情况下，控制车辆沿着x轴方向前进，这便是一个典型的简化方向的路径跟踪问题。假设小车可以以v=0.5m/s的恒定速度向前移动。并且假设小车配备有陀螺仪等传感器，该传感器可以随时测量小车当前的位置（x，y）和方向（角度）。那么本跟踪问题的解决就是需要设计一个跟踪控制器，根据小车的实际位置，调整小