在现代科技飞速发展的当下，红外成像技术凭借其不受光照条件限制、可在复杂环境中实现目标探测等独特优势，被广泛应用于军事侦察、安防监控、医疗诊断、工业检测等众多领域。然而，红外图像往往存在对比度低、噪声干扰大、细节信息模糊等问题，严重影响了后续的目标识别、跟踪和分析等任务的准确性与效率。因此，对红外图像进行有效的增强处理，提升其视觉质量和信息辨识度，成为了该领域亟待解决的关键问题。

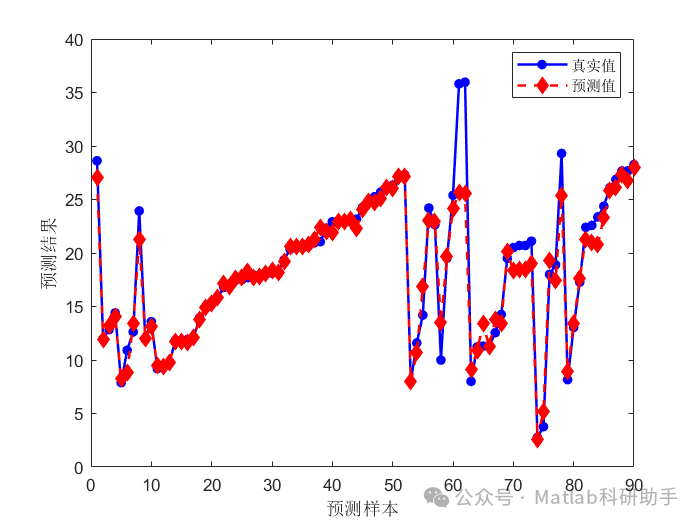
特征选择是机器学习中至关重要的一环，它能够有效地降低模型的复杂度，减少计算量，提升模型的泛化能力，并避免过拟合现象。在众多特征选择算法中，ReliefF算法因其能够处理离散和连续特征，且对特征间相关性具有较好鲁棒性而备受关注。本文将深入探讨ReliefF算法的原理，并结合高效的XGBoost回归模型，给出其在Matlab平台上的完整代码实现，并分析其在实际应用中的优势与不足。一、 ReliefF算

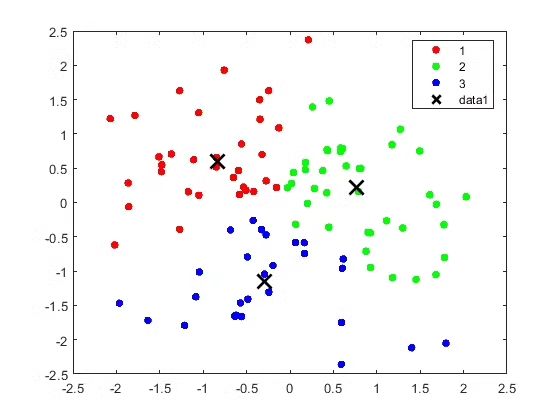
模糊C均值聚类 (Fuzzy C-Means, FCM) 作为一种常用的模糊聚类算法，广泛应用于图像分割、模式识别、数据挖掘等领域。然而，FCM算法的结果通常以隶属度矩阵和聚类中心的形式呈现，难以直观地理解和分析。因此，对FCM聚类结果进行有效可视化至关重要，它能够帮助研究者更好地理解数据结构、评估聚类效果，并为后续分析提供支撑。本文将探讨基于FCM模糊C均值聚类结果的可视化方法，并分析其优缺点及

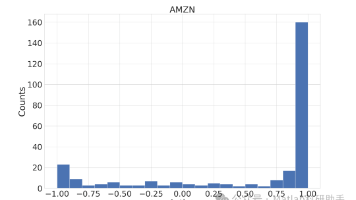
近年来，深度强化学习（DRL）在处理复杂决策任务方面取得了显著进展，尤其是在atari游戏、围棋等离散动作空间领域。然而，现实世界中的许多问题，如机器人控制、自动驾驶、金融交易等，其决策空间往往是连续的。传统的基于离散动作空间的DRL方法难以直接应用于这些领域，或需要进行离散化处理，但这可能导致精度损失和维度灾难。因此，针对连续动作空间的DRL算法研究变得尤为重要。本文旨在深入探讨使用连续动作空间

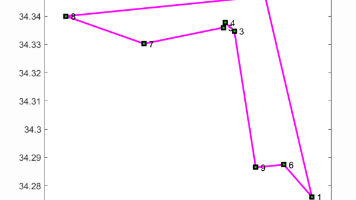
车辆路径问题 (Vehicle Routing Problem, VRP) 作为运筹学领域一个经典的组合优化问题，在物流、配送、交通运输等领域具有广泛的应用价值。其基本目标是在满足一系列约束条件的前提下，为车队规划最优的行驶路线，从而降低成本、提高效率。然而，现实世界的VRP问题往往并非单一简单，而是受到多种约束的制约，并需要同时考虑多个车辆的协调运作，这使得问题的复杂性呈指数级增长。本文将深入探

本文深入探讨了人工势场法（Artificial Potential Field Method, APF）在机器人路径规划领域的理论基础、方法原理及其在实际应用中的优势与局限性。人工势场法作为一种基于虚拟力场的实时避障方法，以其直观、简洁的特性在移动机器人导航、自动化生产等领域得到了广泛关注。文章详细阐述了吸引势场和排斥势场的构建方式，分析了常见的势场函数模型及其参数选择对规划效果的影响。同时，本文

在复杂多变的动态环境中实现高效、安全的路径规划一直是机器人学、自动化领域乃至更广泛的计算机科学领域研究的重点与难点。传统的路径规划算法，如 Dijkstra 算法、A* 算法及其变种，在静态或已知环境下的表现通常令人满意。然而，当面对未知障碍物、动态障碍物或环境信息不完整的情况时，这些算法往往难以应对，暴露出其在实时性和适应性方面的不足。人工势场法（Artificial Potential Fie

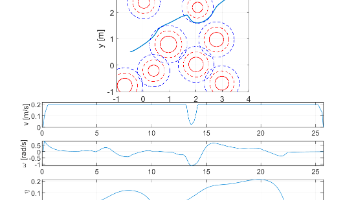
倒立摆系统，作为一个经典的非线性、不稳定控制对象，在控制理论研究和工程实践中具有重要的地位。由于其内在的不稳定性，传统的线性控制方法往往难以取得令人满意的控制效果。近年来，模糊控制理论以其无需精确数学模型、鲁棒性强、易于实现等优势，在倒立摆控制领域得到了广泛的应用。本文将深入探讨基于模糊控制的倒立摆系统设计与实现，从系统建模、模糊控制器的设计、仿真分析以及实际应用等方面进行详细阐述，旨在展示模糊控

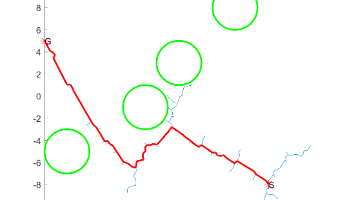
路径规划作为机器人自主导航的核心技术之一，其研究与应用对于提升机器人的智能化水平至关重要。在复杂多变的环境中，机器人需要能够快速、准确地找到一条从起始点到目标点的无碰撞路径，同时满足一定的性能指标，例如最短路径、最平滑路径等。近年来，随着人工智能和计算能力的飞速发展，涌现出众多路径规划算法，其中快速随机树（Rapidly-exploring Random Tree, RRT）算法因其在处理高维空间

噪声污染是信号处理领域中普遍存在且亟待解决的问题。本文深入探讨了一种结合经验模态分解（Empirical Mode Decomposition，EMD）与小波阈值法的混合信号去噪重构方法。EMD能够将复杂的非线性非平稳信号分解为一系列固有模态函数（Intrinsic Mode Functions，IMFs），而小波阈值法则利用小波变换的稀疏性特性来有效抑制噪声。本文首先简述了EMD与小波阈值法的基