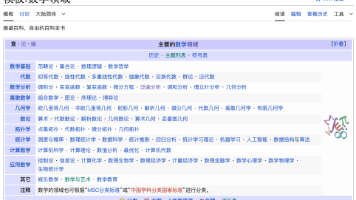
其他学习资料 【转】数学系专业课参考书https://blog.csdn.net/rocvfx/article/details/53316516以下转自 赏悦斋https://www.cnblogs.com/sddai/p/5730529.html随着学习的深入，越发感到数学的重要性。想系统了解数学的各分支，故转此贴！解析几何解析几何有被代数吃掉的趋势，不过就数学系的学生而言...

Hilbert变换解释Hilbert变换从公式上看，是信号与1/(pi*t)的卷积。此外，可以从“线性系统”，“调幅-调频”等角度思考，具体参考如下链接！--------------------------------------Hilbert变换理解-----------------------------------------------------【1】浅显易懂版h...

就是将输入数据 gadm36_USA_0.shp 转换为GMT可识别的 OGR/GMT 格式，输出保存到文件 gadm36_USA_0.gmt 中。

正态分布函数形式：y=normpdf(x,mu,sigma)x - x轴数据，如 x=-10:0.01:10; 注意正态分布，正负对称！mu - 均值，默认为0；sigma - 标准差，默认为1；实例x=-10:0.01:10;y=normpdf(x,0,1);plot(x,y);对数正态分布函数形式：y=lognpdf(x,mu,sigma)x - x轴数据，如 x=0:0.01:10;mu -

fliplr(A)只可用于行向量，列向量不行！实例:(1) 行向量(2) 列向量

1. 属于号 \in2. 求和符号 \sum_{}^{}3. 积分符号 \int_{min}^{max}4. 大于等于、小于等于号导言区使用两个宏包： \usepackage{amsmath} \usepackage{amssymb}大于等于号： \geqslant小于等于号：\leqslant大于号：\textgreater小于号：\textless5. 点乘/除、叉乘/除来自：Markdown

个人小结：显示和隐式区别在于，求解偏微分方程时所采用的数学策略的区别，具体而言，显示是差分，隐式是牛顿迭代。求解方式的差异，必然会有不同的优缺点。隐式 -- 优点是准确，对步长无要求（即，对网格无要求），但存在收敛问题。显示 -- 优点只要计算足够长，肯定能收敛，但是存在累计误差问题，因此对最小步长有要求（即，对网格有要求！）以下 内容转自abaqus版面的总结：显式一般用于动态问题的分析, 对于

1 、生成(0,1)之间服从均匀分布的随机数Excel 函数格式“=rand()”实例注：“=RANDBETWEEN(0,5)” 生成[0,5]之间的服从均匀分布的整数。2、生成服从正态分布的随机数Excel 函数格式“=NORMINV(probability,mean,standard_dev)”参数解释：Probability - 正态分布的概率值，取值范围(0,1)Mean - 算术平均值；

1. 均匀分布函数形式： x=rand(n,m)n - 行数m - 列数生成在0到1之间，满足均匀分布的随机数！实例2. 正态分布函数形式 x=randn(n,m)n - 行数m - 列数生成均值为0，方差为1的标准正态分布实例3. 对数正态分布函数形式 x=lognrnd(mu,sigma,a,b)mu- 对数值的均值（mean of logarithmic values）；mu = log((

注意理解初试分析步，地应力平衡分析步，荷载分析步之间的关系。并明确边界条件，初试应力，荷载分别施加在哪一步，注意从物理的角度理解各分析步对应的边界、荷载条件。如果Geostatic分析步出现不收敛的情况，首先需要检查，用户定义的初始应力和Geostatic分析步中生效的荷载及边界条件是否对应！...