计算机如何建立远程桌面连接有的时候身在远方，想查看或者调用自己狗窝（宿舍或者家）里的机器的文件，怎么办呢？可以通过远程桌面登录自己个的电脑，利用剪切板的功能便可以实现文件之间的传送。当然，假如家里的电脑没开机，可以让别人帮你开一下机，不一定要登录进界面，但是一定要保证有网。通过上网查询，按部就班，感觉自己什么步骤都做了，但是蹦出下面这个界面：咋回事呢？我也不知道，只能再检查一下被远程的机子该

matlab的setfield函数是给结构数组的字段指定值的。有以下两种调用方式：s = setfield(s,'field',value)s = setfield(s,{sIndx1,...,sIndxM},'field',{fIndx1,...,fIndxN},value)第一种就不说了，第二种先看一个程序：grades = [];level = 5;semester = 'Fall';

运筹领域有很多有趣的问题，比如中国邮递员问题，最短路问题等等。lingo在求解规划问题、图与网络问题，对策决策问题，以及存储论等方面的求解有很好的应用。最短路问题model: sets: cities/A,B1,B2,C1,C2,C3,D/; roads(cities,cities)/A B1,A B2,B1 C1,B1 C2,B1 C3,B2 C1, B2 C2,B2 C3,C1 D,C2 D,

vscode 远程连接 docker 容器进行 C++ 代码调试实践vscode 是可以利用远程的编译环境在本地进行打断点调试的。文章目录vscode 远程连接 docker 容器进行 C++ 代码调试实践服务器端创建容器并进行端口映射容器设置vscode 远程连接容器调试服务器端创建容器并进行端口映射docker run -it \--name abacus2 \--workdir /root

分布式优化和去中心化优化概述陆嵩中科院 数学与系统科学研究院 科学与工程计算国家重点实验室文章目录分布式优化和去中心化优化概述简介预备知识优化基础理论梯度下降方法（GD）Gradient Descent步长选取收敛率约束优化问题的拉格朗日乘数法次梯度算法图谱理论基础平均一致性问题模型问题梯度算法收敛性结果对于去中心化的梯度下降方法凸问题的 DGD 算法一些结论和讨论凸问题的较新方法ADMM（原始-

Matlab Simulink仿真工具的应用****Simulink是一个用来对动态系统进行建模、仿真和分析的软件包。使用Simulink来建模、分析和仿真各种动态系统（包括连续系统、离散系统和混合系统），将是一件非常轻松的事情。它提供了一种图形化的交互环境，只需用鼠标拖动的方法便能迅速地建立起系统框图模型，甚至不需要编写一行代码。由于Simulink具有强大的功能与友好的用户界面，因此它已

分布式优化和去中心化优化概述陆嵩中科院 数学与系统科学研究院 科学与工程计算国家重点实验室文章目录分布式优化和去中心化优化概述简介预备知识优化基础理论梯度下降方法（GD）Gradient Descent步长选取收敛率约束优化问题的拉格朗日乘数法次梯度算法图谱理论基础平均一致性问题模型问题梯度算法收敛性结果对于去中心化的梯度下降方法凸问题的 DGD 算法一些结论和讨论凸问题的较新方法ADMM（原始-

学习一门语言有必要系统体系地从头到脚学一遍吗？我认为有必要，但是没意义。如果你有一些其他语言的基础，想要入门 python，那么最好的方式就是了解一下它有哪些数据结构和循环等怎么写，并自己敲一些代码测试一下，剩下的就是直接拿它开始干你想让它帮你做的事，遇到问题面向浏览器编程，一点一点熟悉就好了。下面列出了 python 中最最最基础的数据结构和用法（列表、 numpy 数组等），你花 10 分钟，

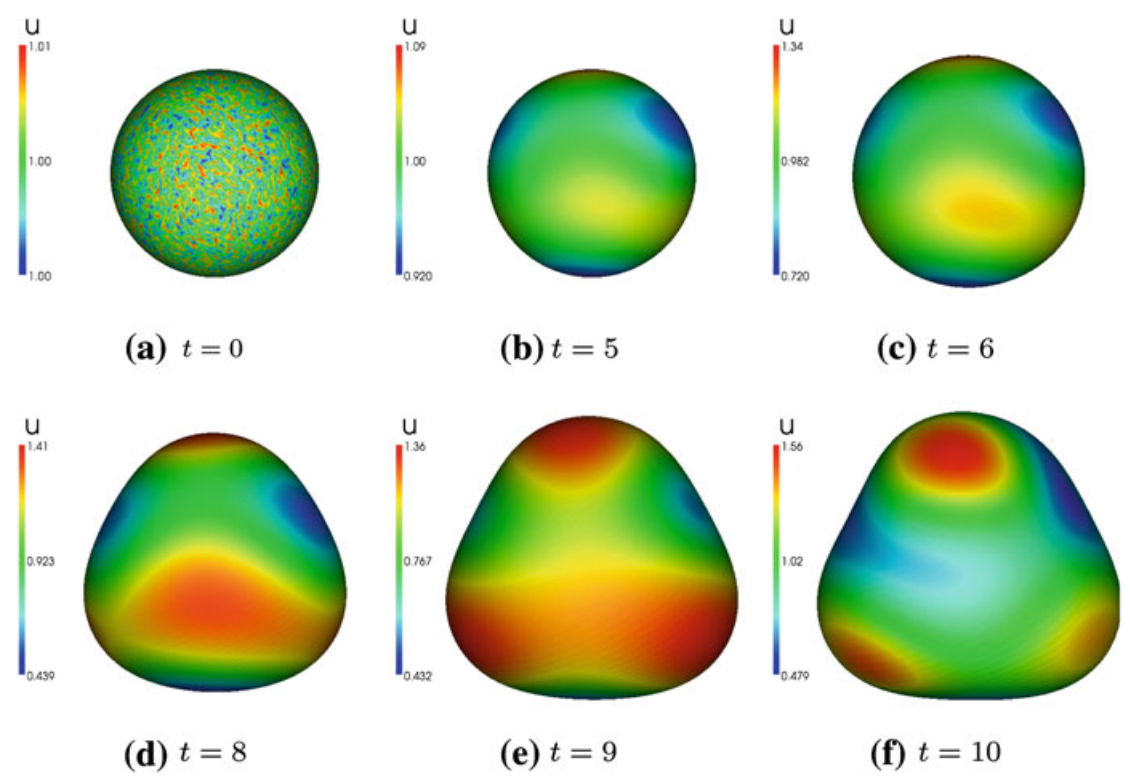
曲面偏微分方程的一个实际应用——肿瘤增长文章目录曲面偏微分方程的一个实际应用——肿瘤增长简介演化表面上反应扩散方程的推导曲面梯度演化表面上的反应扩散系统模型说明曲面有限元方法变分形式演化曲面有限元方法时间离散肿瘤增长模型建立数值方法数值结果网格自适应和重新划分网格简介基本想法是利用表面有限元数值方法求解演化曲面上的反应扩散方程。不断增长的生物表面上的模式形成，是通过求解曲面上的反应扩散方程得到的，

为什么叫插值，为什么叫greedy，可以看得出来，我们选的就是投影之后，距离最大的一个点，然后把它固定。也就是说，我们对于$\mathbf{F}$选行，我们只要计算里面必要分量作用即可，也就是可以把选行操作放到$\mathbf{F}$里面去。POD方法固有的局限性，使得无法很好地处理非线性项，所以必须有一个合适的方法处理非线性项。这里看起来，似乎还需要把非线性项施加于每个分量算出来，其实并不然，这