EdgeShard：通过协作边缘计算实现高效的大语言模型推理

M. Zhang, X. Shen, J. Cao, Z. Cui and S. Jiang, “EdgeShard: Efficient LLM Inference via Collaborative Edge Computing,” in IEEE Internet of Things Journal, vol. 12, no. 10, pp. 13119-13131, 15 May15, 2025, doi: 10.1109/JIOT.2024.3524255.

1. 引言与研究动机

大语言模型（LLMs）的出现代表了人工智能领域的重大突破。OpenAI的GPT-4、Meta的Llama以及Google的PALM等模型都建立在Transformer架构之上，其特点是参数规模巨大（通常达到数千亿个参数）和训练数据量庞大。这种规模使得模型能够捕捉语言和上下文中的复杂模式，产生所谓的"智能涌现"现象。

然而，当前LLM部署面临的核心挑战在于其对云计算的严重依赖。云端部署带来三个主要问题：首先，对云计算的依赖妨碍了实时应用（如机器人控制、导航或探索）所需的快速模型推理能力；其次，传输大量数据（包括文本、视频、图像、音频和物联网传感数据）到云数据中心导致巨大的带宽消耗和网络架构压力；第三，基于云的LLM在处理医院和银行的敏感数据以及手机上的个人数据时引发重大隐私问题。

边缘计算通过在网络边缘部署LLM提供了解决方案，但边缘设备的计算密集性和资源贪婪性带来新挑战。例如，全精度Llama2-7B模型的推理至少需要28GB内存，这可能超过大多数边缘设备的容量。现有研究采用模型量化来减小模型大小，但往往导致精度损失；其他工作倾向于使用云边协作，但云服务器和边缘设备之间的延迟通常很高且不稳定。

2. 生成式LLM推理的基础原理

2.1 推理过程的两阶段特性

基于解码器的LLM推理过程本质上是迭代的，包含两个关键阶段：

预填充阶段（Prefill Phase）：模型接收用户初始令牌序列$(x_1,...,x_n)$作为输入，通过计算概率$P(x_{n+1}|x_1,...,x_n)$生成第一个新令牌$x_{n+1}$。在这个阶段，模型需要同时处理所有输入令牌，计算密集度最高。

自回归生成阶段（Autoregressive Generation）：模型基于初始输入和已生成的令牌，每次生成一个令牌。这个阶段会顺序生成多个迭代的令牌，直到满足停止条件（生成结束序列令牌EOS或达到用户指定/模型约束的最大令牌数）。

2.2 模型架构与KV缓存机制

基于解码器的LLM模型通常由嵌入层、重复的线性连接的Transformer层和输出层组成。由于生成的令牌由序列中所有先前令牌决定，LLM利用键值缓存（KV caching）来避免重复计算。每个Transformer层存储过去的计算以加速响应，从而减少计算工作量并改善响应时间。

预填充阶段生成令牌的时间通常比自回归阶段高10倍，因为预填充阶段需要计算所有输入令牌的KV缓存作为初始化。

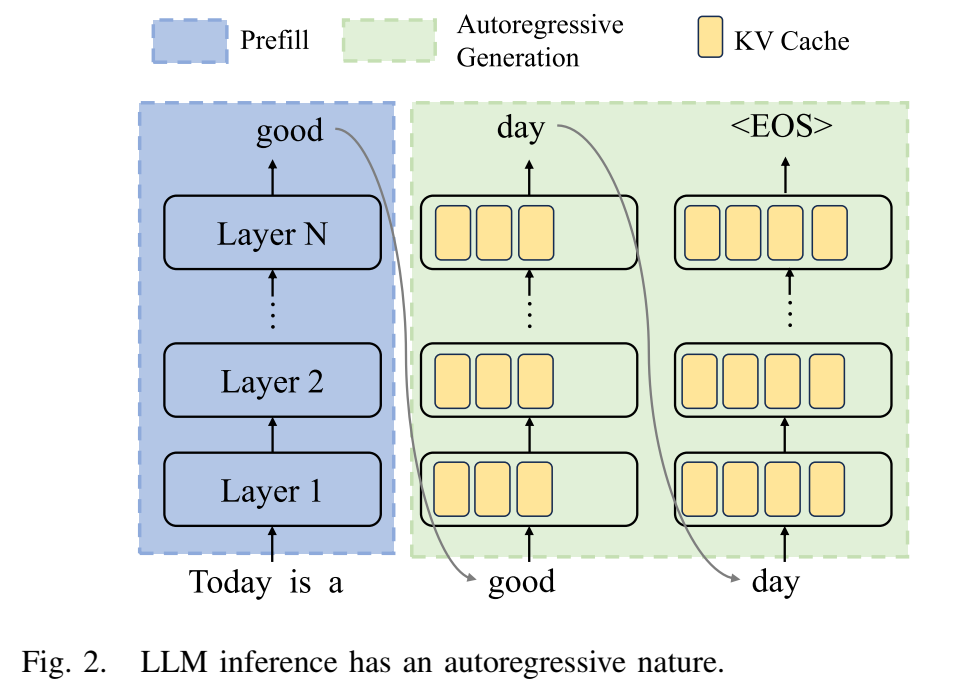
图2描述：该图详细展示了LLM推理的自回归特性。模型包含N层，以一对一的方式处理输入令牌序列并运行所有层来生成令牌。在预填充阶段，模型一次性处理输入"Today is a"，第一个生成的令牌是"good"。在自回归生成阶段，模型首先将"Today is a good"作为输入生成下一个令牌"day"，然后将"Today is a good day"作为输入生成下一个令牌"EOS"，表示生成结束。

3. 协作边缘计算框架

3.1 系统架构概述

协作边缘计算（CEC）最近被提出用于整合地理分布式边缘设备和云服务器的计算资源，以实现高效的资源利用和性能优化。CEC与现有边缘计算研究的区别在于：现有研究关注云、边缘和终端设备之间的垂直协作，而忽略了水平的边缘到边缘协作，导致资源利用未优化、服务覆盖受限和性能不均。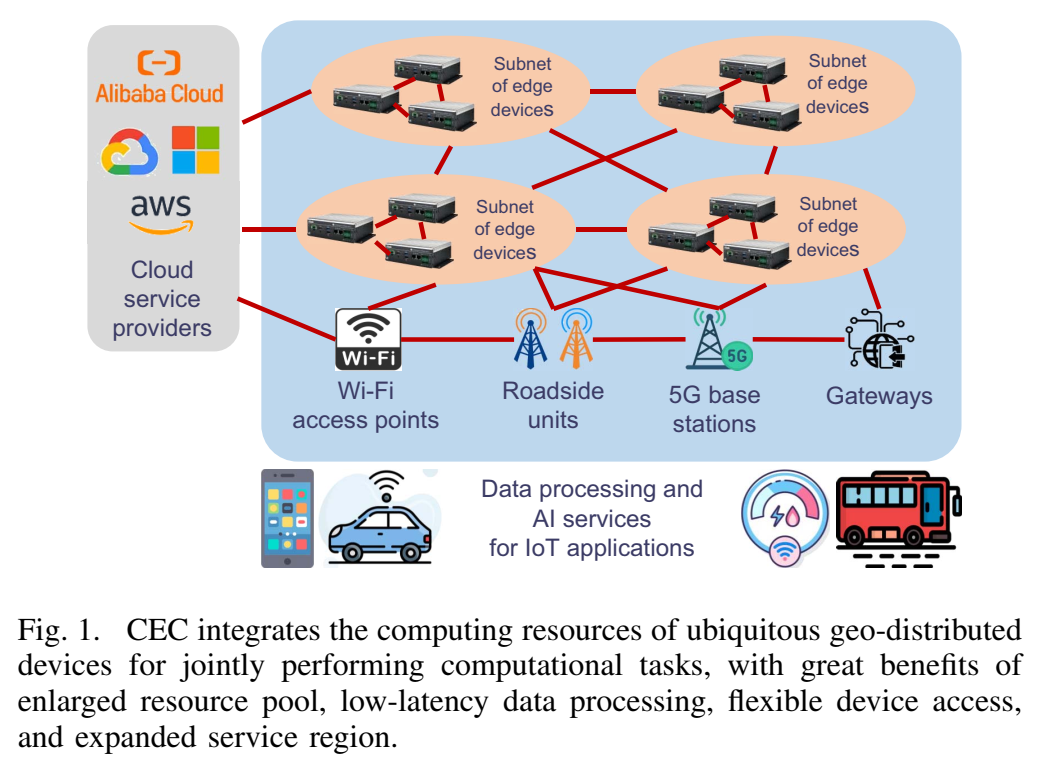

图1描述：该图展示了CEC如何整合无处不在的地理分布式设备的计算资源来共同执行计算任务。图中显示了Wi-Fi接入点、路边单元、5G基站、网关和云服务提供商如何连接形成共享资源池，协作提供即时数据处理和AI服务。多个边缘设备子网通过这种方式为物联网应用提供数据处理和AI服务，具有扩大资源池、低延迟数据处理、灵活设备访问和扩展服务区域等优势。

3.2 EdgeShard框架的三个阶段

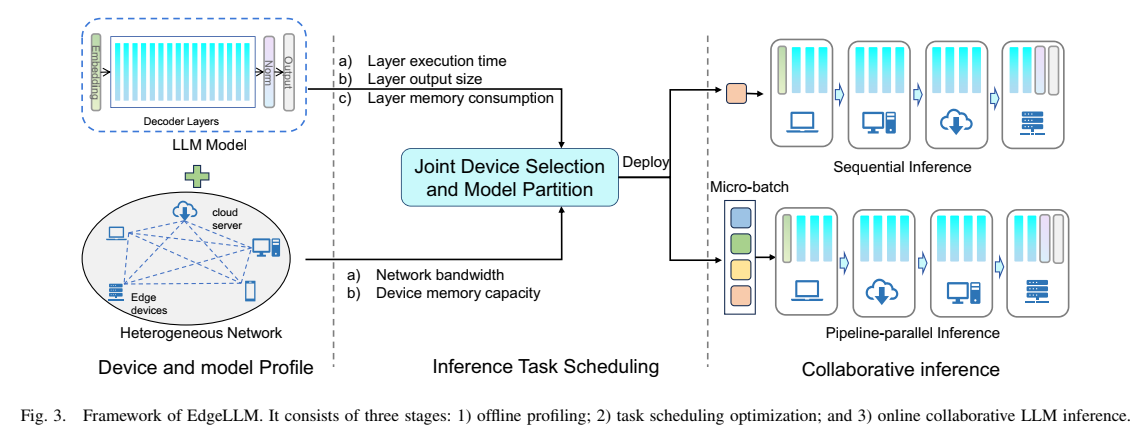
图3描述：该图完整展示了EdgeShard框架，包括三个主要阶段。左侧是设备和模型分析阶段，收集层执行时间、层输出大小、层内存消耗等模型相关信息，以及网络带宽和设备内存容量等异构网络信息。中间是推理任务调度阶段，执行联合设备选择和模型划分优化。右侧是协作推理阶段，展示了顺序推理和流水线并行推理（包括微批处理）两种执行模式。

分析阶段（Profiling）

这是一个离线步骤，只需执行一次。收集的跟踪信息包括：

• 每层在不同设备上的执行时间（分别分析预填充和自回归阶段）
• 每层的激活大小和内存消耗
• 每个设备的可用内存和设备间带宽

对于内存不足以容纳完整模型的设备，使用动态模型加载技术：首先基于模型架构计算每层的内存消耗，根据给定设备的内存预算估计设备可以容纳的最大层数，基于此将模型划分为多个分片并顺序加载到设备中。

调度优化阶段

调度器生成部署策略，确定：

• 哪些设备参与推理
• 如何按层划分LLM
• 模型分片应分配给哪个设备

该策略综合考虑异构资源、设备内存预算和隐私约束。

协作推理阶段

KV缓存管理是关键问题，因为KV缓存的大小会随生成令牌的长度增加。采用贪婪原则预分配内存空间：设分配的Transformer层数为$N_a$，输入令牌的批次大小为$B_b$，输入令牌的最大长度为$I_m$，生成令牌的最大长度为$G_m$，则预分配的KV缓存空间大小为：

$$\text{KV Cache Size}=N_a\cdot B_b\cdot (I_m+G_m)$$

4. 优化问题的数学建模

4.1 系统模型

考虑一个包含$M$个边缘设备和云服务器的网络。LLM模型具有层次架构，包含嵌入层、多个解码器层和输出层，共$N$层。设：

• $O_i$：层$i$的激活大小，$0\le i\le N-1$
• $Re{q}_i$：层$i$的内存消耗
• $Me{m}_j$：设备$j$的内存预算
• $B_{k,j}$：设备$k$和设备$j$之间的带宽，$0\le k,j\le M-1$

源节点（输入令牌所在位置）设为节点0。

4.2 延迟优化问题

问题形式化

使用二进制变量$X_{i,j}$表示LLM分配策略：

$$X_{i,j}=\{\begin{array}{ll}1,& \text{如果层}i\text{分配给节点}j\\ 0,& \text{否则}\end{array}$$

设$t_{comp}^{i,j}$表示层$i$在节点$j$上的计算时间。如果层$i-1$和层$i$分别分配给节点$k$和$j$，则通信时间为：

$$t_{comm}^{i-1,k,j}=\{\begin{array}{ll}\frac{O_{i-1}}{B_{k,j}},& \text{如果 }k\ne j\\ 0,& \text{否则}\end{array}$$

总推理时间为：

$$T_{tol}(X)=\sum _{i=0}^{N-1}\sum _{j=0}^{M-1}{X}_{i,j}\cdot t_{comp}^{i,j}+\sum _{i=1}^{N-1}\sum _{j=0}^{M-1}\sum _{k=0}^{M-1}{X}_{i-1,k}\cdot X_{i,j}\cdot t_{comm}^{i-1,k,j}$$

优化问题形式化为：

$$\underset{X_{i,j}}{\min }{T}_{tol}(X)$$

约束条件：
$$\begin{array}{rl}{X}_{0,0}& =1\text{（隐私约束）}\\ \sum _{i=0}^{N-1}{X}_{i,j}\cdot Re{q}_i& \le Me{m}_j,\forall j\text{（内存约束）}\\ \sum _{j=0}^{M-1}{X}_{i,j}& =1,\forall i\text{（唯一性约束）}\end{array}$$

动态规划解决方案

设$DP(i,j)$表示当层$i$分配给节点$j$时，前$i$层的最小总执行时间。状态转移方程为：

DP(i,j)=min⁡k{DP(i−1,k)+tcompi,j+tcommi−1,k,j+1(i)⋅tcommi,j,0}DP(i,j) = \min_{k} \{DP(i-1,k) + t_{comp}^{i,j} + t_{comm}^{i-1,k,j} + \mathbf{1}(i) \cdot t_{comm}^{i,j,0}\}DP(i,j)=kmin​{DP(i−1,k)+tcompi,j​+tcommi−1,k,j​+1(i)⋅tcommi,j,0​}

其中$1(i)$是指示函数：

$$1(i)=\{\begin{array}{ll}1,& \text{如果 }i=N-1\\ 0,& \text{否则}\end{array}$$

初始化：$DP(0,0)=t_{comp}^{0,0}$

最优解：${\min }_{j=0,...,M-1}DP(N-1,j)$

4.3 吞吐量优化问题

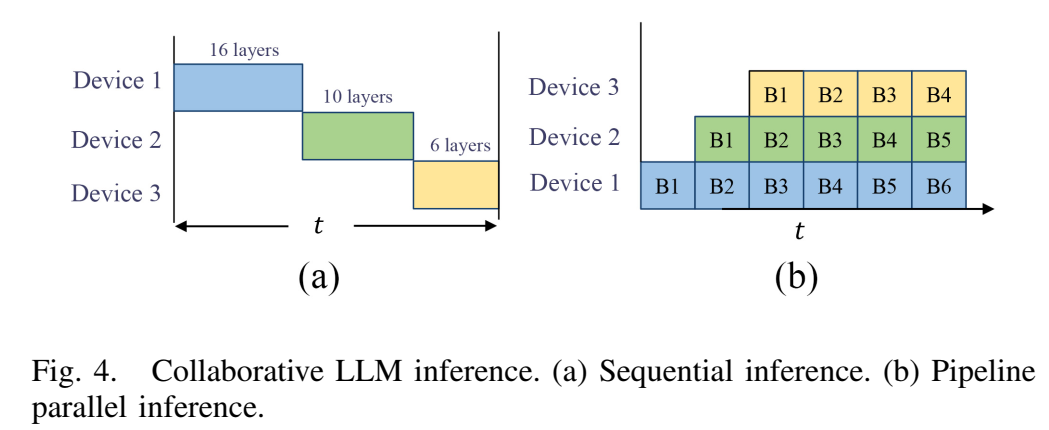
图4描述：该图展示了两种协作LLM推理模式。(a)顺序推理：设备轮流使用分配的模型分片执行计算。以Llama2-7b为例，32层模型被划分为三个分片（层1-16、层17-26、层27-32），分别分配给设备1-3。设备1首先处理输入令牌，然后将激活/输出发送给设备2，设备2处理数据后传输给设备3，设备3将生成的令牌发送回设备1。(b)流水线并行推理：输入数据首先被分割成微批次（B1-B4），设备1处理B1后立即处理B2，同时设备2开始处理B1，实现设备的高利用率。

对于流水线并行推理，设备$j$的最大延迟为：

Tjlatency=max⁡{tcompi→m,j,tcommi−1,k,j}T_j^{latency} = \max\{t_{comp}^{i \rightarrow m,j}, t_{comm}^{i-1,k,j}\}Tjlatency​=max{tcompi→m,j​,tcommi−1,k,j​}

优化问题形式化为：

min⁡Xi,jmax⁡j∈S{Tjlatency}\min_{X_{i,j}} \max_{j \in S}\{T_j^{latency}\}Xi,j​min​j∈Smax​{Tjlatency​}

其中$S$是选定的设备集合。

5. 流水线执行优化策略

5.1 气泡问题分析

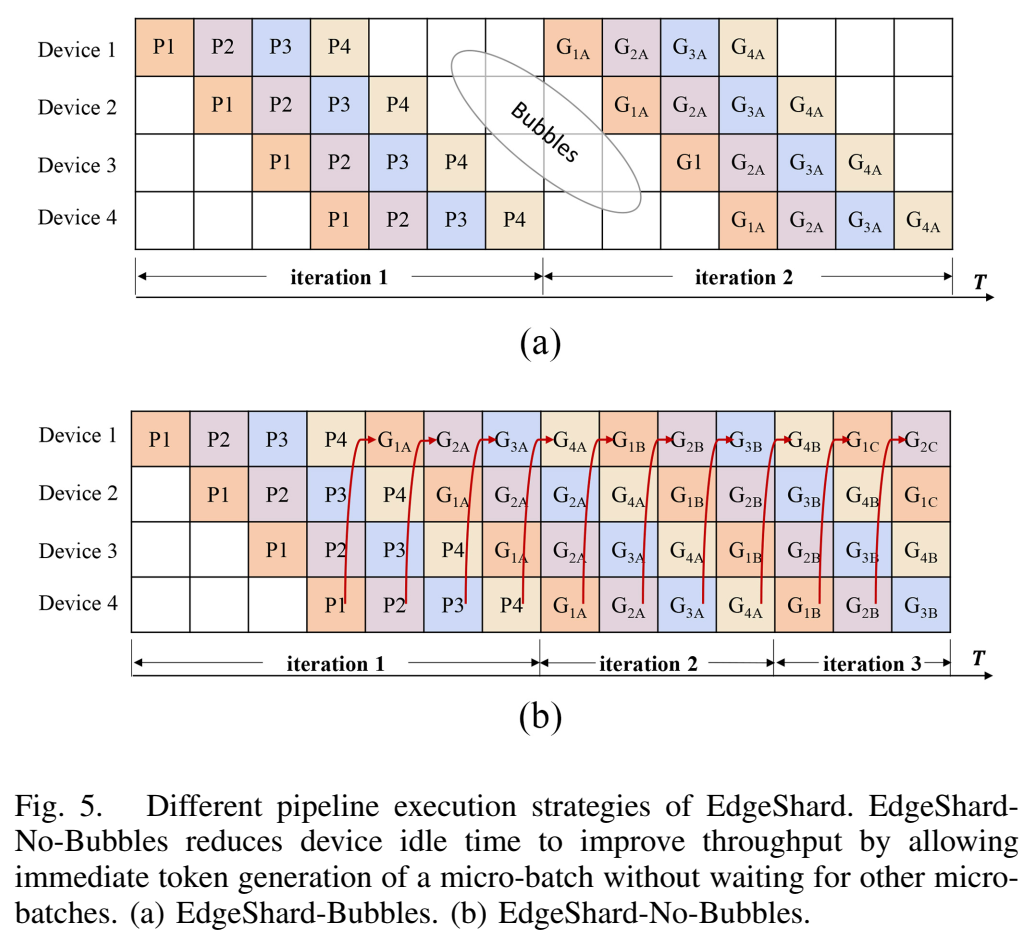
图5描述：该图对比了EdgeShard的两种流水线执行策略。上方(a)展示EdgeShard-Bubbles：P1-P4表示四个微批次的第一次迭代（预填充阶段），G1A和G1B表示第二和第三次迭代（生成阶段的第一和第二次迭代）。G1A必须等待第一次迭代（P4的结束）才能开始，导致设备1-3处于空闲状态的气泡。下方(b)展示EdgeShard-No-Bubbles：P1的预填充阶段结束后，设备1立即执行第一个微批次的令牌生成（G1A），G1A结束后立即进行下一次迭代（G1B），减少了设备空闲时间。

LLM推理的自回归特性导致当前令牌的计算依赖于所有先前令牌，一个迭代必须等待前一个迭代结束并获得先前生成的令牌才能开始，这在流水线并行推理中会导致气泡（设备空闲状态）。

5.2 EdgeShard-No-Bubbles优化

EdgeShard-No-Bubbles优化了跨微批次的令牌生成顺序，允许微批次立即生成令牌而无需等待迭代中所有微批次的结束。这种方法通过减少设备空闲时间来提高资源利用率和吞吐量。

6. 实验评估

6.1 实验环境

图6描述：该图展示了物理测试平台，包含15个设备：12个Jetson AGX Orin（每个具有32GB内存和3.33 TFLOPS计算能力）、2个Jetson Orin NX（每个具有16GB内存和1.88 TFLOPS计算能力）和1个云服务器（配备RTX 3090，24GB内存和36 TFLOPS计算能力）。所有设备通过路由器和交换机连接，设备间基础带宽为1000 Mb/s。

表III - 异构物理设备规格：

类别	设备	内存	AI性能
边缘设备	Jetson AGX Orin	32GB	3.33 TFLOPS
边缘设备	Jetson Orin NX	16GB	1.88 TFLOPS
云服务器	RTX 3090	24GB	36 TFLOPS

6.2 性能结果分析

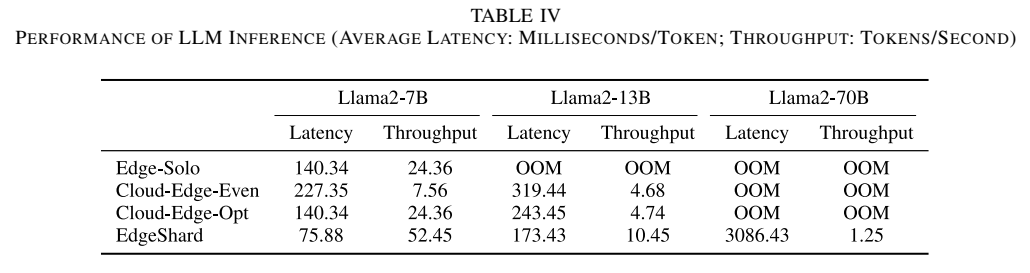
表IV - LLM推理性能展示了详细的实验结果。对于Llama2-7B：

• EdgeShard延迟：75.88 ms/token
• Edge-Solo延迟：140.34 ms/token
• Cloud-Edge-Even延迟：227.35 ms/token
• Cloud-Edge-Opt延迟：140.34 ms/token
• EdgeShard吞吐量：52.45 tokens/s（批次大小8）
• Edge-Solo吞吐量：24.36 tokens/s

对于Llama2-70B，只有EdgeShard能够成功部署（3086.43 ms延迟，1.25 tokens/s吞吐量），其他方法均因内存不足（OOM）而失败。

6.3 带宽影响分析

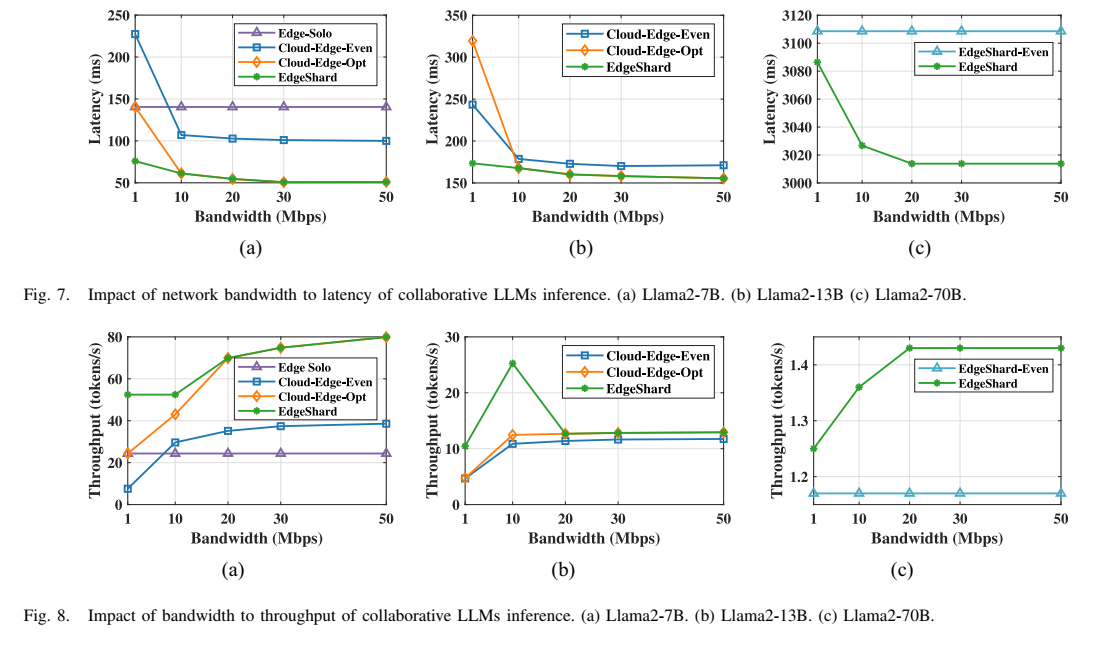
图7和图8描述：这两组图展示了网络带宽对延迟和吞吐量的影响。图7显示了三个模型（7B、13B、70B）的延迟随带宽变化情况。当带宽从1 Mb/s增加到10 Mb/s时，延迟显著降低；从10 Mb/s到50 Mb/s时，延迟变化较小，表明带宽逐渐饱和。图8展示了吞吐量的变化，EdgeShard在所有带宽条件下都优于基线方法。

带宽分析的关键发现：

• 带宽低于10 Mb/s时，数据传输成为瓶颈
• 带宽高于10 Mb/s后，计算时间成为主要瓶颈
• Cloud-Edge-Opt在1 Mb/s带宽时退化为本地执行

6.4 源节点影响分析

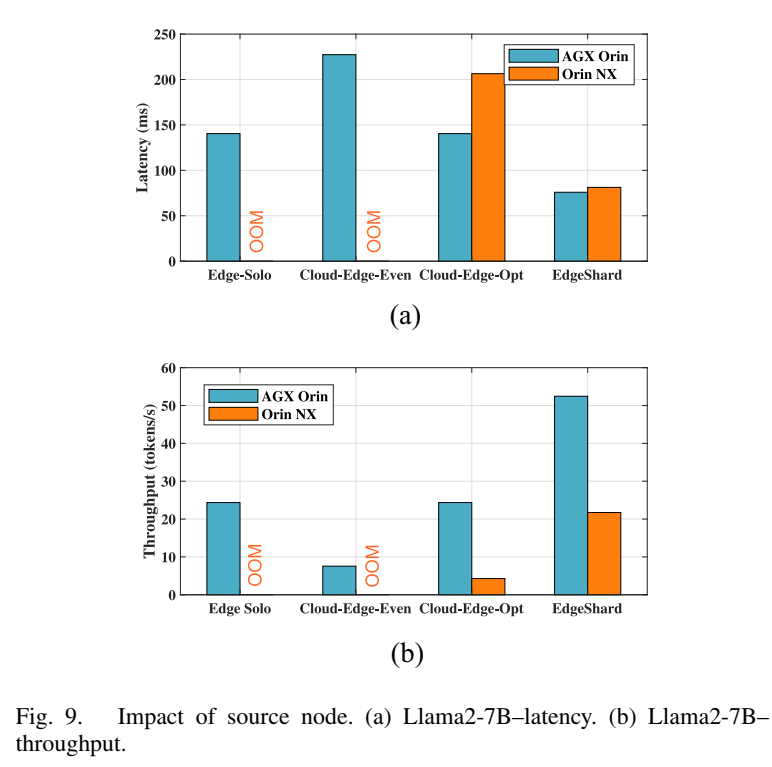
图9描述：该图对比了使用AGX Orin和Orin NX作为源节点时的性能差异。(a)延迟对比：AGX Orin作为源节点时，EdgeShard延迟约75ms；Orin NX作为源节点时，延迟约80ms。Cloud-Edge-Opt方法的差异更明显（约60ms差距）。(b)吞吐量对比：AGX Orin的吞吐量优势在EdgeShard中被缩小（仅2倍差异），而在Cloud-Edge-Opt中达到6倍差异。

源节点的计算能力对性能有显著影响，但EdgeShard通过涉及更多设备并在源节点上放置更少的模型层，能够填补源节点之间的计算能力差距。

6.5 分析策略影响

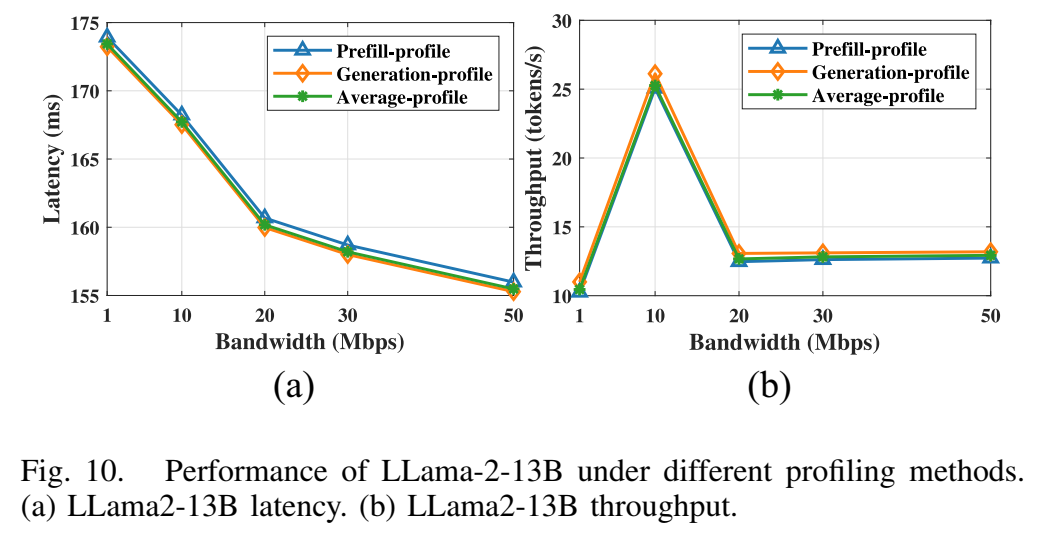
图10描述：该图展示了不同分析方法对Llama2-13B推理性能的影响。(a)延迟比较：预填充分析、生成分析和平均分析三种方法的延迟差异较小。(b)吞吐量比较：三种方法的吞吐量表现相似。尽管预填充和生成阶段存在10倍的执行时间差异，但不同计算设备的相对计算能力保持不变。

6.6 流水线执行策略对比

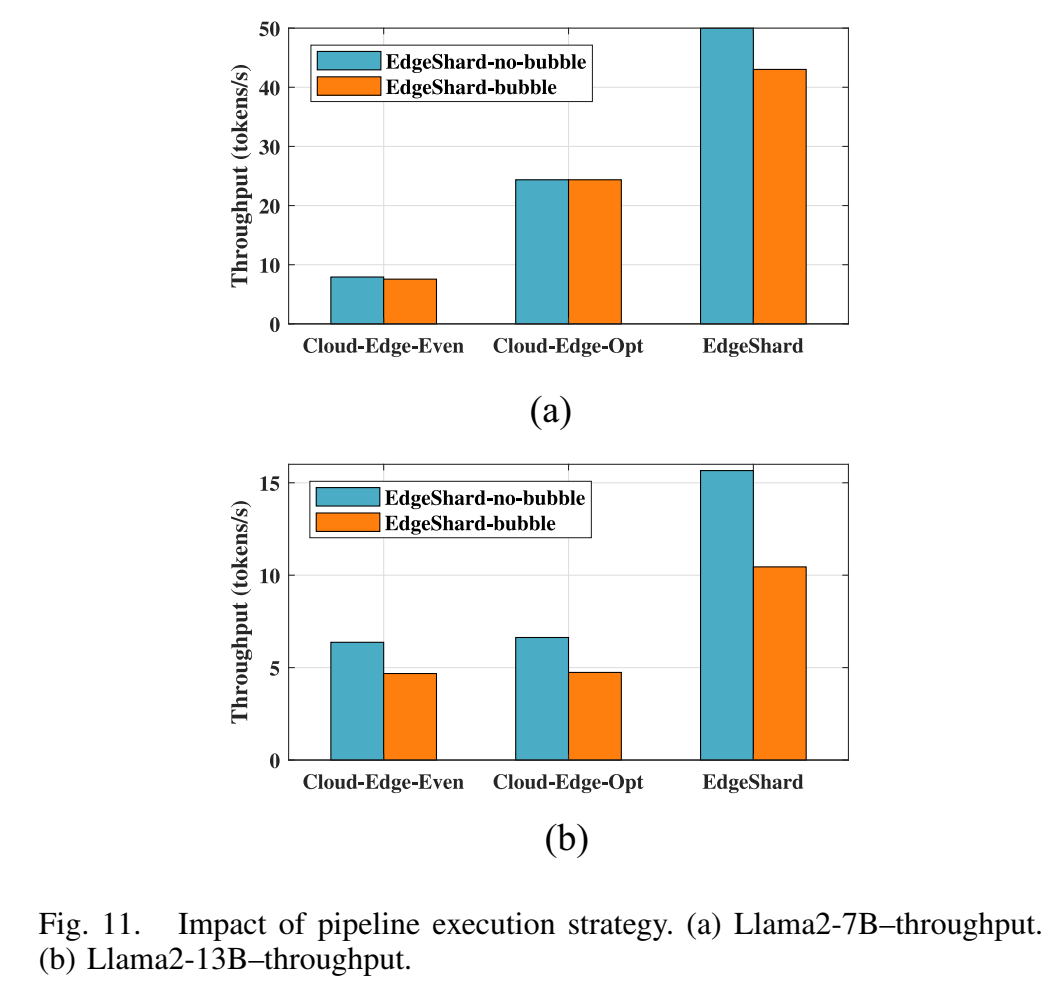
图11描述：该图对比了两种流水线执行策略的吞吐量性能。(a)Llama2-7B：EdgeShard-No-Bubble比EdgeShard-Bubble提高了6.96 tokens/s。(b)Llama2-13B：EdgeShard-No-Bubble比EdgeShard-Bubble提高了5.21 tokens/s。EdgeShard-No-Bubble通过不等待迭代中所有微批次的完成，有效减少了设备空闲时间。

7. 相关工作对比

EdgeShard与现有工作的主要区别：

1. 与云端LLM部署的区别：云服务器通常配备同构GPU并通过高带宽网络（如InfiniBand和NVlinks，带宽可达600 GB/s）连接，而边缘设备本质上具有异构计算能力，通过异构和低带宽网络（几十Kb/s到1000 Mb/s）连接。

2. 与小规模DNN划分的区别：之前的工作只考虑固定数量设备上的模型划分问题，而EdgeShard更进一步，执行联合设备选择和模型划分。

3. 与模型量化方法的区别：量化方法通过降低精度来减小模型大小，但会导致性能下降；EdgeShard保持全精度推理，无精度损失。

8. 结论与未来工作

EdgeShard是在协作边缘计算环境中部署LLM的开创性工作。通过智能的设备选择和模型划分，EdgeShard在各种异构网络条件下实现了自适应的最优部署策略。实验结果表明，EdgeShard实现了高达50%的延迟降低和2倍的吞吐量提升。

---

附录A：动态规划算法的推导

A.1 延迟优化的最优子结构证明

定理：LLM推理延迟优化问题具有最优子结构性质。

证明：设$OPT(i,j)$表示前$i$层的最优分配方案，其中层$i$分配给节点$j$。假设存在更优的前$i-1$层分配方案$OP{T}^{\prime }(i-1,k^{\prime })$，使得：

$$OP{T}^{\prime }(i-1,k^{\prime })+t_{comp}^{i,j}+t_{comm}^{i-1,k^{\prime },j}<OPT(i-1,k)+t_{comp}^{i,j}+t_{comm}^{i-1,k,j}$$

这与$OPT(i-1,k)$是前$i-1$层的最优分配矛盾。因此，最优解可以从子问题的最优解构造。

A.2 吞吐量优化的状态空间分析

对于吞吐量优化，状态空间大小为$O(N\times 2^M\times M)$，其中：

• $N$：模型层数
• $2^M$：所有可能的设备子集
• $M$：最后使用的设备

状态转移的时间复杂度分析：

• 对于每个状态$(i,S,k)$，需要考虑$O(N-i)$个可能的下一层
• 对于每个下一层$m$，需要考虑$O(M-|S|)$个未使用的设备
• 总时间复杂度：$O(N^2\times 2^M\times M^2)$

A.3 KV缓存内存计算的推导

设Transformer层的参数：

• $d_{model}$：模型维度
• $n_{heads}$：注意力头数
• $d_{head}=d_{model}/n_{heads}$：每个头的维度
• $se{q}_{len}$：序列长度

每个Transformer层的KV缓存大小：

$$\text{KV Cache per layer}=2\times se{q}_{len}\times d_{model}\times \text{precision}$$

其中因子2来自Key和Value两个矩阵。

对于批次大小$B$和$N_a$个分配的层：

$$\text{Total KV Cache}=N_a\times B\times 2\times (I_m+G_m)\times d_{model}\times \text{precision}$$

A.4 通信时间的分析

考虑层$i$的激活传输，激活大小$O_i$通常为：

$$O_i=B\times se{q}_{len}\times d_{model}\times \text{precision}$$

通信时间包含两部分：

1. 传输延迟：$t_{latency}=RTT/2$
2. 传输时间：$t_{transfer}=O_i/B_{k,j}$

总通信时间：

$$t_{comm}^{i,k,j}=t_{latency}+t_{transfer}=\frac{RTT}{2}+\frac{O_i}{B_{k,j}}$$

在低带宽场景下，传输时间占主导；在高带宽场景下，传输延迟成为瓶颈。

A.5 流水线并行的气泡时间分析

设流水线深度为$D$（设备数），微批次数为$B_{micro}$。

EdgeShard-Bubbles的气泡时间：

Tbubble=(D−1)×max⁡j∈S{Tjstage}×(Gtokens−1)T_{bubble} = (D-1) \times \max_{j \in S}\{T_j^{stage}\} \times (G_{tokens} - 1)Tbubble​=(D−1)×j∈Smax​{Tjstage​}×(Gtokens​−1)

其中$G_{tokens}$是生成的令牌数，$T_j^{stage}$是设备$j$的阶段执行时间。

EdgeShard-No-Bubbles的气泡时间：

Tbubbleoptimized=(D−1)×max⁡j∈S{Tjstage}T_{bubble}^{optimized} = (D-1) \times \max_{j \in S}\{T_j^{stage}\}Tbubbleoptimized​=(D−1)×j∈Smax​{Tjstage​}

优化后的气泡时间与生成令牌数无关，显著提高了设备利用率。

附录B：算法复杂度的详细分析

B.1 算法1（延迟优化）的空间复杂度

动态规划表$DP(i,j)$的空间需求：$O(N\times M)$

选择表$choice(i,j)$的空间需求：$O(N\times M)$

总空间复杂度：$O(N\times M)$

B.2 算法2（吞吐量优化）的优化策略

原始算法的指数级复杂度可以通过以下策略优化：

1. 剪枝策略：如果当前状态的最大延迟已经超过已知最优解，提前终止
2. 贪婪近似：限制考虑的设备数量为$K$个最优候选
3. 分层优化：先确定设备数量，再优化分配

优化后的复杂度可降至$O(N^2\times K\times M^2)$，其中$K\ll 2^M$。