2.各个数据根据他们到每个聚类中心的距离选择中心最近的聚类分配到其中。3.重新计算各个聚类中的所有数据的平均值，并将得到的结果作为新的中心；1.在数据集中随机选择K个数据用来做K个聚类的初始中心。4.重复上述操作直至。

将其中最具有代表性的特征提取出来，提取方法常见有最大池化和平均池化，分别取区域中的最大值或者平均值代表最具代表性的特征。卷积层：提取图像的底层特征，在存在特征的区域确定高值，不存在的区域确定低值，计算其与卷积核的乘积值来确定得到特征图（卷积核通过在输入图像的二维矩阵上不停的移动，每一次移动都进行一次乘积的求和，作为此位置的值。），整个卷积过程是一个降维过程，通过卷积核的不停移动计算，可以提取图像中

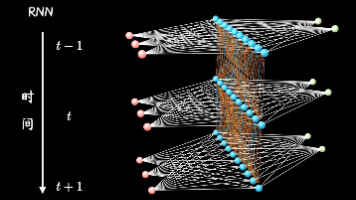
循环神经网络由输入层、隐藏层、输出层组成。输入层接受传入数据；隐藏层既接收当前时刻的输入，也接收上一时刻隐藏层的状态作为额外输入，这种结构允许RNN对序列中的每个元素执行相同的操作，同时保持一个“记忆”状态，这个状态会随着序列的推进而更新；输出层基于隐藏层的状态生成输出。这样的设计使LSTM能够在长时间跨度内保留重要的信息，同时也能够选择性地忘记不相关的信息。的方法，按照标准的反向传播算法进行权重

输出层通常只包含一个节点，该节点的值为加权求和层的输出除以非线性求和层的输出。），输入数据经过隐藏层的径向基函数从原始的输入空间映射到一个高维的特征空间，在高维空间中进行线性或非线性的操作；输出层将隐含层的输出进行线性组合，产生最终的输出。加权求和层计算所有模式层节点输出的加权和，非线性求和层计算所有加权值的非线性函数值。输出层从求和层提供的信息中确定最终的分类结果，选择具有最大后验概率的类别作为

的强化学习算法，用于解决具有高维状态空间的问题。基于当前观察到的状态，智能体选择一定策略决定采取的动作，根据每个动作的价值分配一个选择的概率，价值越高的动作被选中的概率越大，所有动作都有可能会被选择。基于新获得的状态和奖励，智能体采用一定的价值函数更新其对当前策略的价值评估：时序差分学习、蒙特卡洛方法、动态规划方法。智能体执行动作后，观察环境对其动作的响应，接收新的状态和相应的奖励，奖励是标量值，

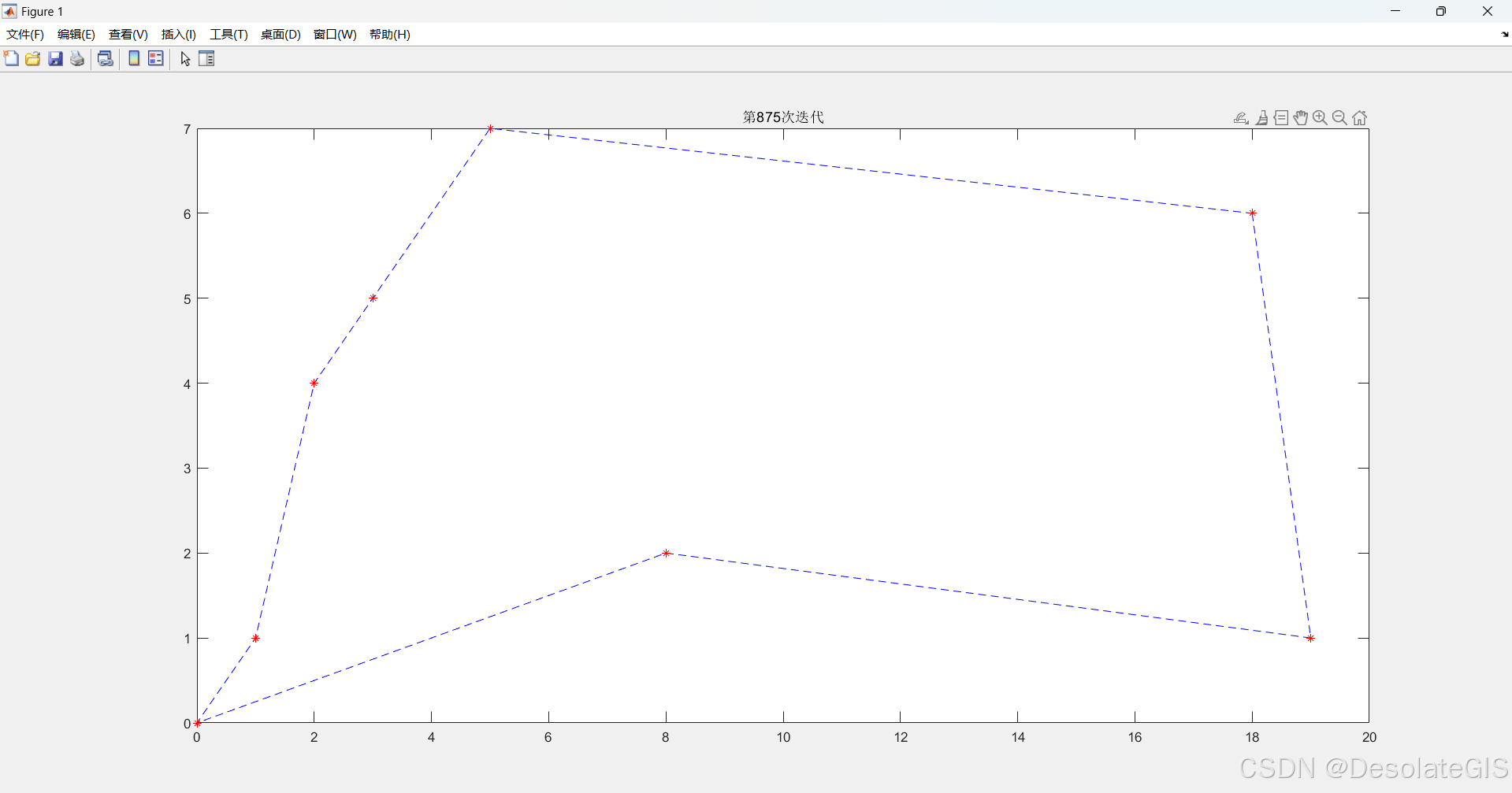
TSP问题（旅行商问题）是指旅行家要旅行n个城市，要求各个城市经历且仅经历一次然后回到出发城市，并要求所走的路程最短。下面用模拟退火算法解决该问题。

先随机取出一个样本放入采样集中，再把该样本放回初始数据集中，使得下次采用时该样本扔有可能被选中，这样经过多次随机采样操作，我们得到含有全部样本的采样集，初始数据集中有的样本多次出现，有的则从未出现。用Pearson相关性分析模型计算出各指标与洪水发生概率的相关性系数，相关性系数越高的与洪水发生概率的相关性越大。3.递归构建决策树并计算特征重要性，找到特征重要性最大的指标为与洪水发生概率具有强相关性

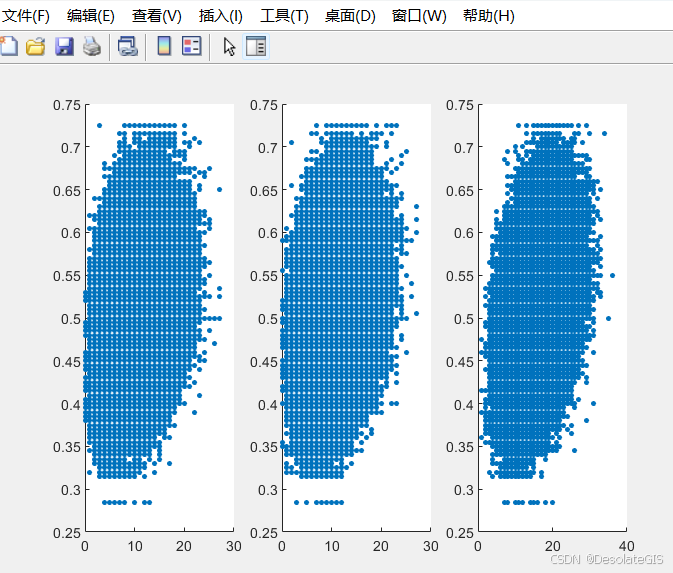
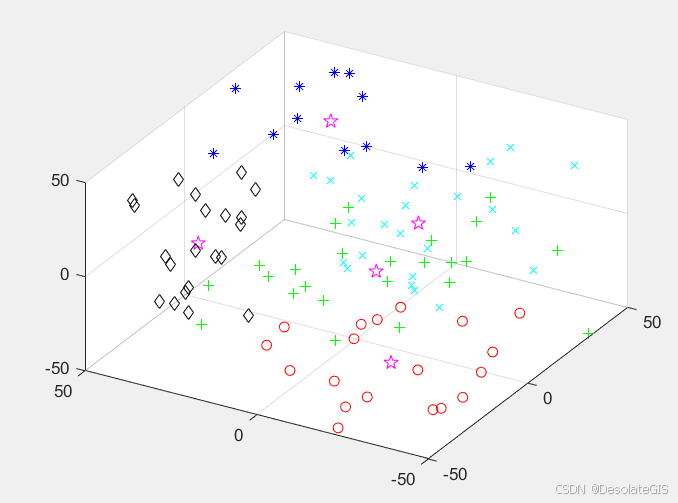
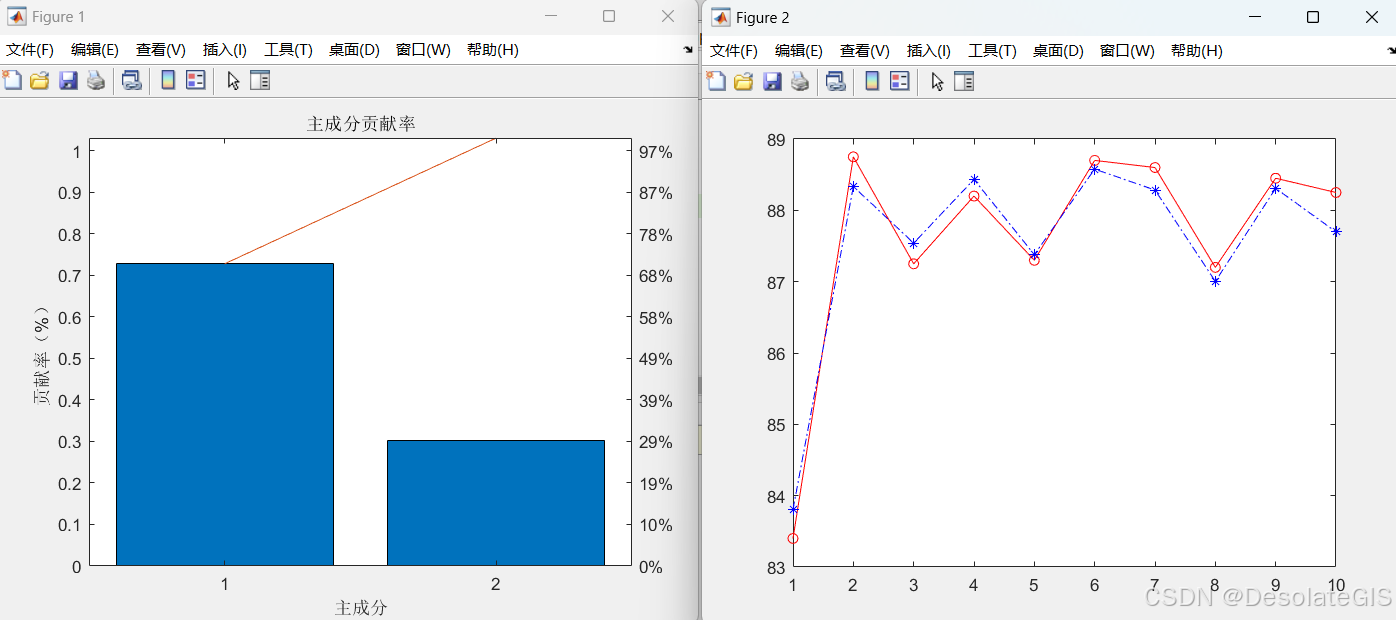
PCA的思想是将n维特征映射到m维上（m<n），这m维是全新的正交特征，称为主成分，这m维的特征是重新构造出来的，不是简单的从n维特征中减去n-m维特征。：计算自变量和因变量的协方差矩阵，通过迭代算法（如NIPALS算法）提取出第一组主成分，这组主成分既能反映自变量的变化趋势，又能反映因变量的变化趋势。：对剩余的自变量残差继续提取新的主成分，并进行回归，直到满足预定的停止准则（如累计解释变异率达到

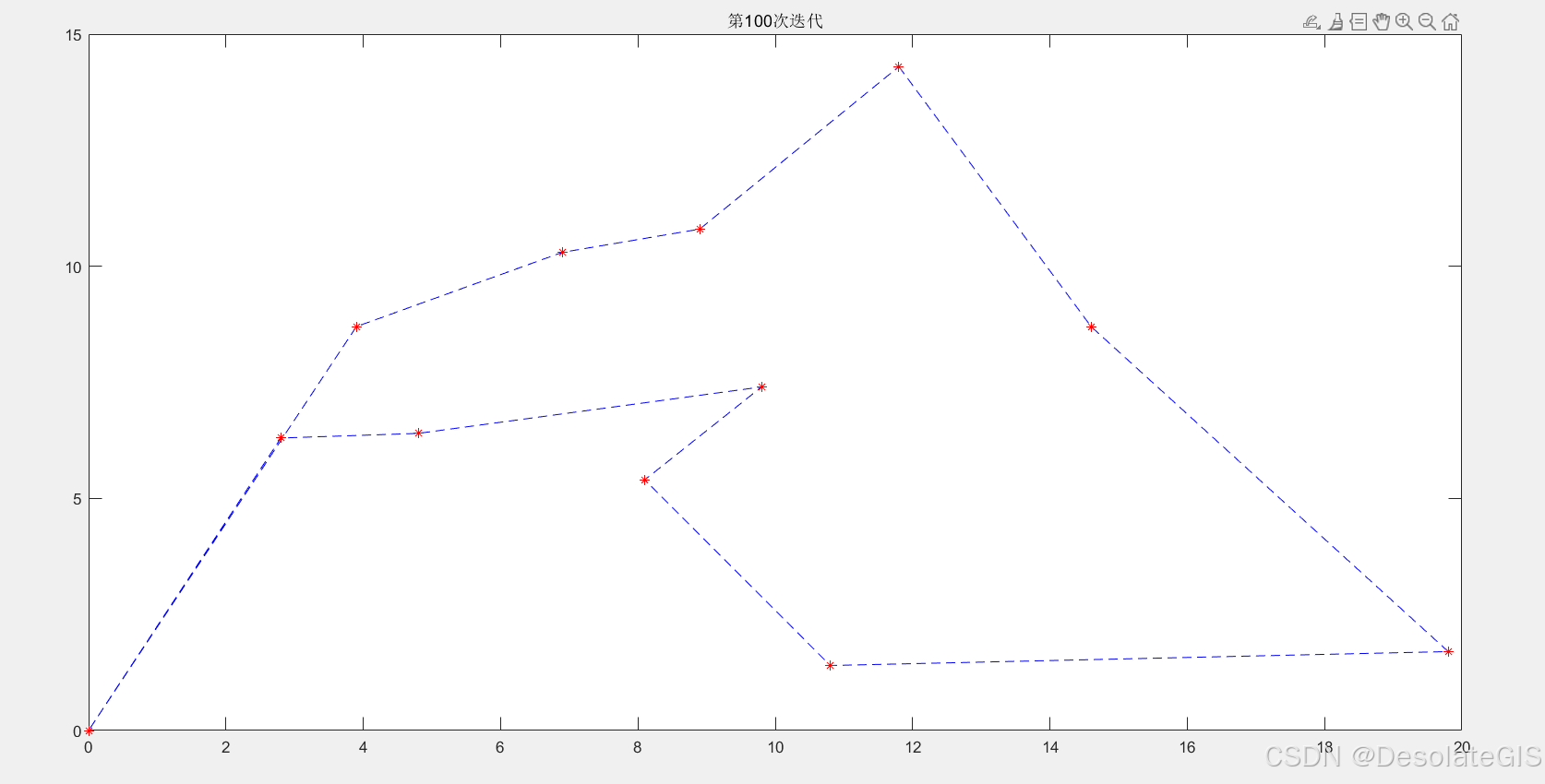
TSP问题（旅行商问题）是指旅行家要旅行n个城市，要求各个城市经历且仅经历一次然后回到出发城市，并要求所走的路程最短。下面用蚁群算法解决该问题。

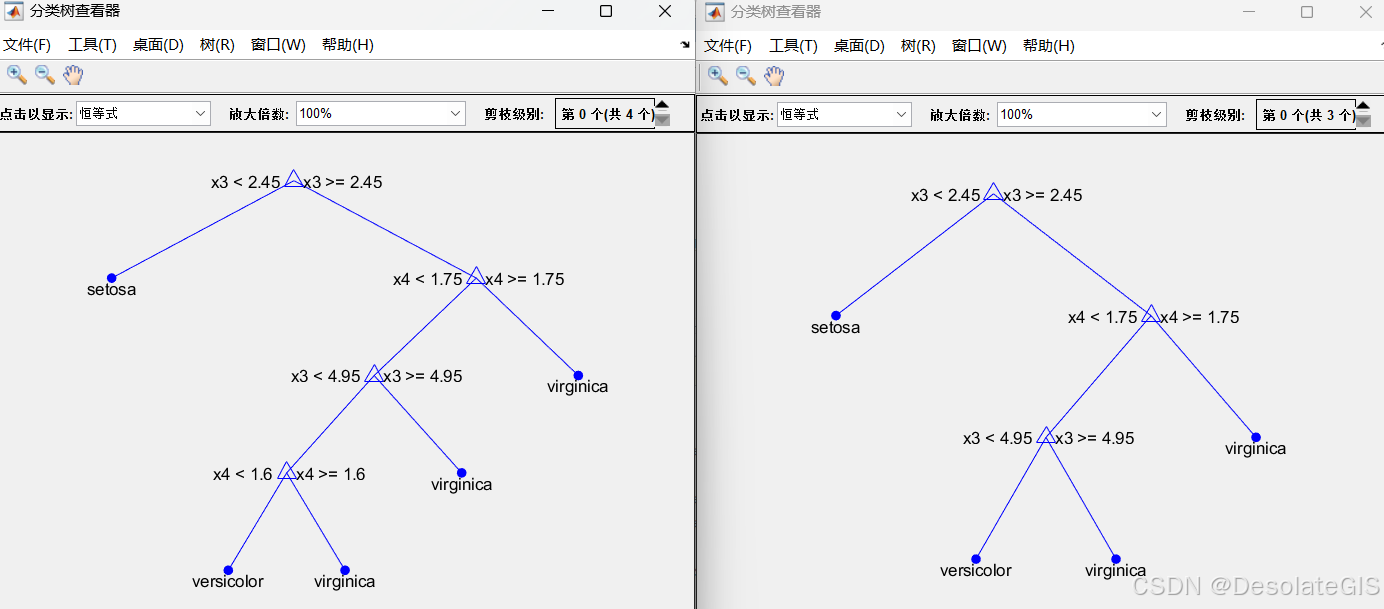
决策树（Decision Tree）是一种分类和回归方法，是基于各种情况发生的所需条件构成决策树，以实现期望最大化的一种图解法。由于这种决策分支画成图形很像一棵树的枝干，故称决策树。以Fisher 1936 年的鸢尾花数据为例，构建决策树。对比测试数据的预测值与实际值确定该决策树的精准度。