大模型基础 | dropout机制
Dropout机制摘要 Dropout是一种有效的神经网络正则化技术,通过随机"丢弃"部分神经元(概率p)来防止过拟合。其核心原理包括:1)作为模型集成方法,训练多个子网络;2)减少神经元依赖,增强特征鲁棒性。训练时需引入1/(1-p)的缩放因子保持期望一致,但会增大方差。AlphaDropout通过仿射变换调整丢弃值,保持数据统计特性。这种机制简单高效,能显著提升模型泛化能力
Dropout机制
Dropout是一种简单而强大的正则化技术。
Dropout源于发表于2014年的论文"Dropout:A Simple Way to Prevent Neural Networks fromOverfitting”,是一种在神经网络中用于减少过拟合的技术。它通过在训练过程中以一定概率随机“丢弃”网络中的部分神经元及其连接边,迫使网络学习更具稳健的特征,从而提高模型的泛化能力。
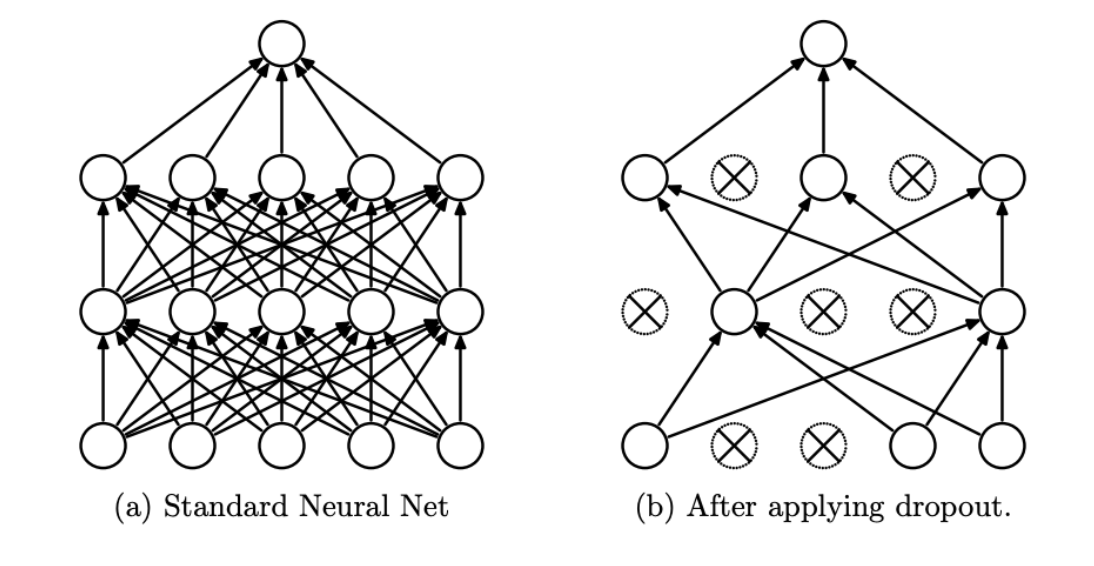
Dropout原理
比如神经元的结果为S,加上Dropout机制之后,输出为 S ′ S' S′。具体公式如下:
S ′ = S ∗ d S' = S * d S′=S∗d
变量 d 服从参数为p的二项分布,其概率表达式函数为:
d = { p d = 0 1 − p d = 1 (1) d = \begin{cases} p & d = 0 \\ 1 - p & d = 1 \end{cases} \tag1 d={p1−pd=0d=1(1)
服从以概率p取0和以概率1-p取1的二项分布,也叫伯努利分布
Dropout解释
- 模型集成的角度。Dropout可以视为一种Bagging集成学习方法。在每次训练迭代中,它会随机“丢弃”一部分神经元,这可以视为在每次迭代中创建了一个不同的子网络。在训练过程中,这些子网络会学习到不同的特征和模式。当这些子网络的预测结果被平均或集成起来时,可以利用多个子网络的优势,减少方差误差,进而降低模型过拟合的情况。
- 学习更具稳健特征的角度。Dropout在每次训练迭代中随机将部分神经元的输出置为0,这样可以减少不同神经元之间的复杂依赖关系,即网络不能依赖于任何一个神经元的单一输出。这一过程有助于网络学习到更加稳健的特征表示,即能够在多种“结构”下都有效的特征。
Dropout训练和预测
我们在使用Dropout时,训练阶段只是部分网络起作用,而预测阶段所有网络都参与计算,因此会有所不同。
期望计算
Dropout在训练阶段,会根据二项分布的公式,输出如下结果
E x = ( 1 − p ) ∗ x + p ∗ 0 = ( 1 − p ) ∗ x E_{x} = (1-p)* x + p*0 = (1-p) * x Ex=(1−p)∗x+p∗0=(1−p)∗x
Dropout在推理阶段,所有权重都参与计算,没有权重被丢弃,
E x = x E_{x} = x Ex=x
可以得到,Dropout训练阶段和推理阶段是不一致的,一个推理阶段是完整的x,训练阶段是1-p概率的x。
而可以通过一个缩放因子,即乘以或者除以的数值,达到训练和推理一致的效果。
比如训练时缩放 1 / ( 1 − p ) 1 / (1-p) 1/(1−p)而预测保持不变
E x = 1 / ( 1 − p ) ∗ ( 1 − p ) ∗ x + p ∗ 0 = x E_{x} =1 / (1-p)* (1-p)* x + p*0 = x Ex=1/(1−p)∗(1−p)∗x+p∗0=x
同样也可以预测时缩放(1-p),训练时保持不变
E x = ( 1 − p ) ∗ x = ( 1 − p ) x E_{x} = (1-p) * x = (1-p) x Ex=(1−p)∗x=(1−p)x
方差计算
如上结论可得缩放因子:为了保持训练和推理阶段的期望一致,在训练时通常会引入一个缩放因子 1 1 − p \frac{1}{1-p} 1−p1
方差是衡量一组数据或一个随机变量与其期望值(均值)偏离程度的指标,定义为“各数据与均值之差的平方的期望”,即:
D [ x ′ ] = E [ ( x ′ − E [ x ′ ] ) 2 ] = E [ ( x ′ ) 2 ] − ( E [ x ′ ] ) 2 (1) D[x'] = E[(x' - E[x'])^2] = E[(x')^2] - (E[x'])^2 \tag1 D[x′]=E[(x′−E[x′])2]=E[(x′)2]−(E[x′])2(1)
先计算 E [ ( x ′ ) 2 ] E[(x')^2] E[(x′)2]:
E [ ( x ′ ) 2 ] = E [ ( 1 1 − p ⋅ d ⋅ x ) 2 ] = 1 ( 1 − p ) 2 ⋅ E [ d 2 ] ⋅ E [ x 2 ] E[(x')^2] = E\left[\left(\frac{1}{1-p} \cdot d \cdot x\right)^2\right] = \frac{1}{(1-p)^2} \cdot E[d^2] \cdot E[x^2] E[(x′)2]=E[(1−p1⋅d⋅x)2]=(1−p)21⋅E[d2]⋅E[x2]
因为 d d d 是二值变量, d 2 = d d^2 = d d2=d,所以 E [ d 2 ] = E [ d ] = 1 − p E[d^2] = E[d] = 1 - p E[d2]=E[d]=1−p,代入得:
E [ ( x ′ ) 2 ] = 1 ( 1 − p ) 2 ⋅ ( 1 − p ) ⋅ E [ x 2 ] = 1 1 − p ⋅ E [ x 2 ] E[(x')^2] = \frac{1}{(1-p)^2} \cdot (1-p) \cdot E[x^2] = \frac{1}{1-p} \cdot E[x^2] E[(x′)2]=(1−p)21⋅(1−p)⋅E[x2]=1−p1⋅E[x2]
又因为 E [ x ′ ] = E [ x ] E[x'] = E[x] E[x′]=E[x],所以公式(1)可得:
D [ x ′ ] = 1 1 − p ⋅ E [ x 2 ] − ( E [ x ] ) 2 (2) D[x'] = \frac{1}{1-p} \cdot E[x^2] - (E[x])^2 \tag2 D[x′]=1−p1⋅E[x2]−(E[x])2(2)
利用 E [ x 2 ] = D [ x ] + ( E [ x ] ) 2 E[x^2] = D[x] + (E[x])^2 E[x2]=D[x]+(E[x])2,公式(2)代入:
D [ x ′ ] = 1 1 − p ⋅ ( D [ x ] + ( E [ x ] ) 2 ) − ( E [ x ] ) 2 D[x'] = \frac{1}{1-p} \cdot (D[x] + (E[x])^2) - (E[x])^2 D[x′]=1−p1⋅(D[x]+(E[x])2)−(E[x])2
展开:
D [ x ′ ] = 1 1 − p ⋅ D [ x ] + 1 1 − p ⋅ ( E [ x ] ) 2 − ( E [ x ] ) 2 D[x'] = \frac{1}{1-p} \cdot D[x] + \frac{1}{1-p} \cdot (E[x])^2 - (E[x])^2 D[x′]=1−p1⋅D[x]+1−p1⋅(E[x])2−(E[x])2
合并后两项:
D [ x ′ ] = 1 1 − p ⋅ D [ x ] + ( 1 1 − p − 1 ) ⋅ ( E [ x ] ) 2 D[x'] = \frac{1}{1-p} \cdot D[x] + \left( \frac{1}{1-p} - 1 \right) \cdot (E[x])^2 D[x′]=1−p1⋅D[x]+(1−p1−1)⋅(E[x])2
化简:
D [ x ′ ] = 1 1 − p ⋅ D [ x ] + p 1 − p ⋅ ( E [ x ] ) 2 D[x'] = \frac{1}{1-p} \cdot D[x] + \frac{p}{1-p} \cdot (E[x])^2 D[x′]=1−p1⋅D[x]+1−pp⋅(E[x])2
最终方差公式:
D [ x ′ ] = 1 1 − p ⋅ D [ x ] + p 1 − p ⋅ ( E [ x ] ) 2 \boxed{D[x'] = \frac{1}{1-p} \cdot D[x] + \frac{p}{1-p} \cdot (E[x])^2} D[x′]=1−p1⋅D[x]+1−pp⋅(E[x])2
这个公式说明:使用 Dropout + 缩放因子后,输出的方差不仅与原始方差 D [ x ] D[x] D[x] 有关,还与原始期望的平方 ( E [ x ] ) 2 (E[x])^2 (E[x])2 有关,除非 E [ x ] = 0 E[x] = 0 E[x]=0,否则方差会被放大。
如需进一步简化(例如在 BatchNorm 后 E [ x ] = 0 E[x]=0 E[x]=0),则:
若 E [ x ] = 0 , ⇒ D [ x ′ ] = 1 1 − p ⋅ D [ x ] \text{若 } E[x] = 0, \quad \Rightarrow \quad D[x'] = \frac{1}{1-p} \cdot D[x] 若 E[x]=0,⇒D[x′]=1−p1⋅D[x]
仿射变换
仿射变换(Affine Transformation)是线性代数和几何学中的一个重要概念,广泛应用于计算机图形学、图像处理、机器学习等领域。
你可以把仿射变换理解为:
“保持直线和平行性的线性变换 + 平移”
也就是说,仿射变换不会把直线变成曲线,也不会让原本平行的线变得不平行,但它可以拉伸、旋转、翻转、缩放、剪切,还能整体平移图形。
在数学上,一个从向量空间 R n \mathbb{R}^n Rn 到 R m \mathbb{R}^m Rm 的变换 (f) 是仿射变换,当且仅当它可以表示为:
f ( x ) = A x + b f(\mathbf{x}) = A\mathbf{x} + \mathbf{b} f(x)=Ax+b
其中:
- x \mathbf{x} x 是输入向量(比如一个点的坐标);
- A A A 是一个 m × n m \times n m×n 的矩阵,代表线性变换部分(如旋转、缩放、剪切等); - b \mathbf{b} b 是一个 m m m 维的平移向量;
- A x A\mathbf{x} Ax 是线性变换, b \mathbf{b} b 是平移 —— 两者合起来就是仿射变换。相当于仿射变换是包含线性变换的
** 常见的仿射变换类型(2D图像中):**
| 变换类型 | 说明 | 是否仿射? |
|---|---|---|
| 平移(Translation) | 整体移动图形 | ✅ 是 |
| 旋转(Rotation) | 绕某点旋转 | ✅ 是 |
| 缩放(Scaling) | 放大或缩小 | ✅ 是 |
| 剪切(Shear) | 倾斜变形 | ✅ 是 |
| 反射(Reflection) | 镜像翻转 | ✅ 是 |
| 投影(Perspective) | 透视变形(如近大远小) | ❌ 不是(是非线性变换) |
AlphaDropout
在 AlphaDropout 中,仿射变换被用来调整被“丢弃”的神经元输出值,使得:
- 被设为 − α ′ -\alpha' −α′ 的值,经过变换后,整体输出的均值和方差保持不变。
- 这样网络在训练时即使随机丢弃神经元,也不会破坏数据的统计特性(比如均值=0,方差=1),从而更稳定地训练。
f ( x ) = a ( x ( 1 − d ) + α ′ d ) + b f(x) = a \left( x(1-d) + \alpha' d \right) + b f(x)=a(x(1−d)+α′d)+b
其中:
- d d d是一个与 p p p 相关的变量,表示在 AlphaDropout 中实际被设置为特定值 $ -\alpha’ $的概率。具体来说,在 AlphaDropout 中,神经元的输出不是简单地设置为 0,而是设置为某个特定的值 α ′ \alpha' α′。因此, d d d 实际上是神经元被设置为 − α ′ -\alpha' −α′的概率。
- x ( 1 − d ) + α ′ d x(1-d) + \alpha'd x(1−d)+α′d 是对输入的“选择性替换”(类似Dropout);
- 然后乘以缩放因子 a a a,再加上偏移 b b b —— 这就是标准的仿射变换形式!
更多推荐
 已为社区贡献2条内容
已为社区贡献2条内容






所有评论(0)