本篇目的：Android16进阶之音频播放定位MediaPlayer.seekTo调用流程与实战。在多媒体开发中，精准控制播放进度是提升用户体验的关键。是 Android 框架提供的用于调整播放位置的核心 API。调用层级核心职责关键特性/影响应用框架层参数封装与状态检查支持多种SeekMode定位模式选择系统服务层跨进程传递定位请求保证指令按序到达引擎处理层清空 Decoder 队列与重新索引N

本篇目的：Android tinyalsa 深度解析之pcm_stop调用流程与实战。特性详情描述状态机迁移强制回退。将状态从 RUNNING 直接打回至 SETUP。执行速度极快。直接操作硬件寄存器停止 DMA，不考虑数据完整性。数据安全性丢弃模式。Buffer 中尚未发送到 Codec 的数据会被全部丢弃。对比 Drainpcm_stop是立即切断；pcm_drain是等待数据播放完后再优雅停

本篇目的：Android ALSA驱动进阶之设置访问掩码snd_pcm_access_mask_set：用法实例基本概念snd_pcm_access_mask_set用于设置PCM访问掩码，指定驱动支持的访问模式，如MMAP、RW等，用户空间根据掩码选择访问方式。功能支持设置MMAP、RW、MMAP_VALID等模式；与snd_pcm_access_mask_test配合使用；可内联调用；返回值为

本篇目的：Android ALSA驱动进阶之获取采样格式位宽snd_pcm_format_width：用法实例基本概念snd_pcm_format_width根据enum snd_pcm_format返回采样格式的位宽，用于计算缓冲大小、DMA传输字节数、数据转换等场景。功能支持S8到FLOAT_LE全部格式；返回采样位宽；与内核print格式无缝兼容；可内联调用；返回值为int。使用限制传入值必

本篇目的：Android内核进阶之设置PCM流参数snd_pcm_sw_params：用法实例基本概念snd_pcm_sw_params负责配置起始阈值、可用阈值、停止阈值、唤醒间隔等软件级行为，决定何时自动启动、何时唤醒用户空间、何时停止，与硬件参数无关。功能支持设置start_threshold、stop_threshold、avail_min、silence_size、tstamp_mode

一、前言Android开发者常常面临的一个问题就是防破解、 防二次打包。现如今安全问题越来越重要,越来越多的Android开发者也开始寻求安全的保护方案。请看一下下面的几张图片：1.1u=2065152164,360269629&fm=173&s=D19EA0725C3578880C719942030030F5&w=639&h=342&img...

转自：http://blog.csdn.net/p106786860/article/details/54566583一、Android Things简介Google在近期推出了物联网操作系统Android Things，它可以运行在有线扬声器、智能温控器、安全摄像头、路由器等设备上，Google的理念是通过Android Things让Android开发者与公司能够以他们过去的开

原址2016 年 12 月，Google 发布了 Developer Preview 版的 Android Things，该平台为利用 Android 这一世界上最受支持的操作系统的强大功能构建物联网产品铺平了广阔的道路。但它并不是一个全新的操作系统，而是通过同样是 Google开发的物联网操作系统 Brillo 改进优化的一个操作系统。。今天，就跟大家说说 Android Thin

本篇目的：本课程基于Android15最新版本，深度讲解音频策略系统的设计架构与实战应用。从音频策略树的基础结构入手，逐步深入核心骨架、音量曲线等关键模块。再通过7个真实项目案例（Speaker改向、USB无损播放、蓝牙空间音效、定制音量曲线、Gain转换、数字耳机适配等）完整演示策略开发全流程。最后涵盖系统APP与MediaProjection的音频截取对比，帮助开发者掌握系统级音频策略定制能力

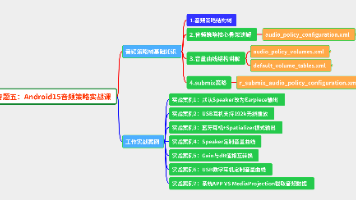
本篇目的：本课程基于Android15最新版本，深度讲解音频策略系统的设计架构与实战应用。从音频策略树的基础结构入手，逐步深入核心骨架、音量曲线等关键模块。再通过7个真实项目案例（Speaker改向、USB无损播放、蓝牙空间音效、定制音量曲线、Gain转换、数字耳机适配等）完整演示策略开发全流程。最后涵盖系统APP与MediaProjection的音频截取对比，帮助开发者掌握系统级音频策略定制能力