本文系统介绍了Word2Vec词向量表示学习算法及其在图数据挖掘中的应用。首先阐述了向量化表示的重要性，指出Word2Vec是NLP领域的基础工具，也是图机器学习算法Node2Vec的前身。文章详细解析了Word2Vec的两种模型架构（CBOW和Skip-gram）和两种优化方法（层次Softmax和负采样），通过大量代码示例展示了实现过程。 重点内容包括：1）向量化表示的核心思想是将离散符号映射

史上最通俗易懂的强化学习入门文章。马尔可夫决策过程就是：智能体根据策略π(a|s)采取行动(行动可以是确定的行动也可以是有概率分布的随机行动)-->系统根据当前状态和行动进行状态转移Pa(这个转移也可以是确定性转移，也可以是系统内部制造的随机转移，形成概率分布)-->系统根据新的状态s'给agent发奖励。如此反复的过程，就是马尔可夫决策过程。

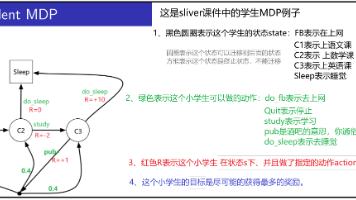
本篇开启无模型(Model-free)强化学习方法：蒙特卡洛学习、时序差分学习、TD(λ)。其中，TD(λ)方法可以看作是蒙特卡洛方法和时序差分方法的混合。这三个方法的最终目的都是用来评估和优化价值函数的，通俗的说就是计算状态价值的。评估价值函数就是计算出那个收敛的Vπ，有了Vπ就可以算出Qπ，有了Qπ就可以用贪婪的方法去提升策略了，如此循环就可以找到最优策略。也就是智能体从小白变成了高手。

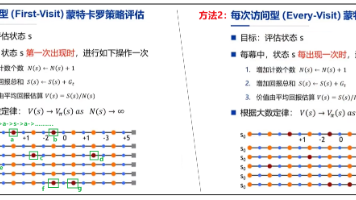
在完备的马尔可夫决策过程中，DP可用于计算价值函数，有了价值函数就可以得到动作价值，有了动作价值就可以得到智能体的策略。但是强化学习的最终目标是找到最优策略，所以基于动态规划的强化学习可以分两种方法寻找最优策略：策略迭代(policy Iteration)和价值迭代(Value Iteration)。下面针对这两种方法分别来讲。

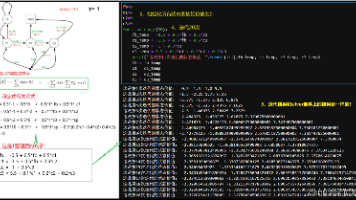
史上最通俗易懂的强化学习入门文章。马尔可夫决策过程就是：智能体根据策略π(a|s)采取行动(行动可以是确定的行动也可以是有概率分布的随机行动)-->系统根据当前状态和行动进行状态转移Pa(这个转移也可以是确定性转移，也可以是系统内部制造的随机转移，形成概率分布)-->系统根据新的状态s'给agent发奖励。如此反复的过程，就是马尔可夫决策过程。

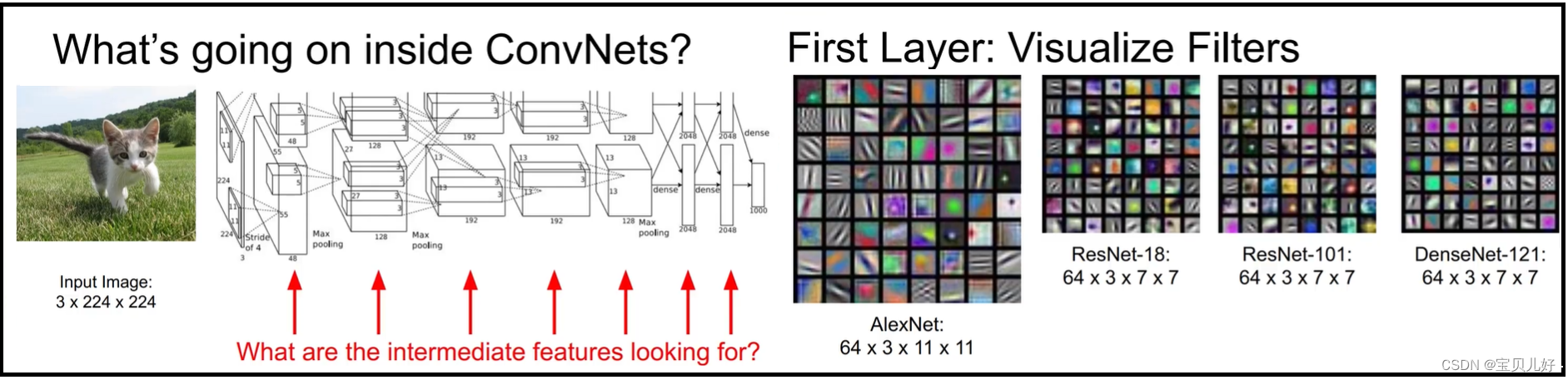
十七、卷积网络可视化至此，不管是分类任务还是检测任务还是生成任务，我们都已经学了各个任务中的经典网络。那为什么这些架构有效呢？其中可视化是最直观的解释，所以本章讲讲可视化。 可视化可以让我们人类直观的看到卷积网络中到底发生了什么：1、神经网络第一层卷积层的卷积核组的可视化：从上图可以看出，不管是简单的alexnet还是复杂的densenet,它的第一层学的模板(卷积核组)都是一些简单的基元，比如点

六、模型效果评估前面讲过，最初我们建模的目的就是预测，最早人们使用的是传统的数理统计分析建模，这是一套完整的理论，是建立在基本假设、总体、样本、抽样、估计、检验等概念框架之上，有一系列完整的数学方法和和数理统计工具去计算统计量，进而得到总体规律而形成的统计模型，然后用模型来进行预测。但是，机器学习和深度学习是没有这一套系统的理论框架的，机器学习和深度学习更像是一个实证类方法，评估一个模型的好坏看预

计算预测样本与训练样本之间的距离，找出与预测样本最近的K个训练样本的标签，然后以少数服从多数的原则（majority-voting），将预测样本与K个最邻近样本中所属类别占比较多的归为一类。其指导思想是“近朱者赤，近墨者黑”，即由你的邻居来推断出你的类别。（2）KNN是一个惰性模型，就是它不用提前学习，当开始预测时，逐个遍历训练数据进行距离计算。（5）注意标签，标签必须是数值型，而且必须是一维的。

思来想去，根据这个指标的业务背景，就是商户的商户的细分品类，其实这个特征是非常非常重要的，可以代表信用卡主对哪种商品的喜好，所以这里我就把这个特征处理成信用卡用户的“刷卡集中度”这个指标，就是用商户的种类/刷卡次数，反应客户是经常在集中的几种商品上刷卡还是分散很多很多商品上刷卡，如果集中度很高，就说明这个客户最喜欢某种商品，如果集中度很低，就说明这个客户的爱好广泛。交易表中除了card_id外，共

的PyTorch的扩展库，几何深度学习指的是应用于图和其他不规则、非结构化数据的深度学习。是非常随意的，它不像MLP、CNN、RNN、Transformer那样，必须要数据规整、要resize、要截断填补等，图神经网络要求的数据只要有点有边就行，至于几个点几条边都随意。然而在真实世界中，并不是所有的事物都可以用结构化数据来表示，比如社交网络、知识图谱、电商购物、复杂的文件系统、蛋白质相互作用关系、