密码学中的decision问题：从两个不同分布中取一个数，来判断该结果来自于哪个分布。比如这个地方就需要分辨收到的y是情况1还是情况2.密码学中的search问题：给定隐藏超平面问题（hidden hyperplanes problem,HHP），让你求向量s。这两个问题之间可实现归约，也就是所谓的search-decision归约。该方案的语义安全可以归约到HHP问题。紧接着，HHP问题又可以归

在1998年，有关多项式环密码系统NTRU被提出。Ajtai提出了原始的SIS问题。在2002年，Micciancio发现可以将这两者结合，提出了效率更高的密码学上问题，也就是本文章将要介绍的SIS问题，已经对应的函数。在格密码专栏中，我将陆续更新Ring-SIS问题的定义，它与原始SIS问题的关系，其在最坏情况（worst case）下的困难性分析。而且还包含在环结构下，形成一个新的概念叫理想格

接下来介绍的算法最早由Klein提出，他将BDD问题的解码半径优化到了：其中k的范围如下：随机化的BDD算法的复杂度为：可以看到当k为常数时，该算法即为多项式时间复杂度。我们知道标准的串行干扰消除算法中会用到就近取整，这一步可以进行优化。

线性代数有两大基础问题：如果A为对角阵的话，那么问题就很好解决。需要注意的是，矩阵的基础行变换会改变特征值的大小。在已知解的情况下，可以利用矩阵行列式解决问题。根据Cramer定则：将以下矩阵的行列式看成一个多项式：该多项式的根即为特征值。当矩阵维度较高时，这个方法就很难计算。

对偶格（dual lattice）也被称之为倒易格（reciprocal lattice）。原来满秩的格写做，其对偶格的定义如下：原来的格点和对偶格的任意（这两个字非常重要）格点相乘为整数即可。原来的格点如果为整数，那么对偶格里有可能会出现小数。此处代表n维实数空间，更准确来讲，对偶格应该在原来格的扩展空间内。那么对偶格更准确的定义，如下：对偶格的右上角经常带“*”,代表格的扩展空间。对偶格的重心

在1986年，L.Babai曾提出最近平面算法来解决CVP问题，利用n代表格的秩，该算法的输出近似值如下：CVP问题的六种变式，如下：当时，后三种问题就与前三种一样了。如果解决了计算问题，由于计算、优化和Gap问题三者困难性一样，那么剩下的优化和Gap问题也就可以解决了。最近平面算法可以解决计算CVP问题，且此时，为了简化分析的思路，后续仅仅讨论，通过修改算法相关的参数也可以达到想要的近似值。简单

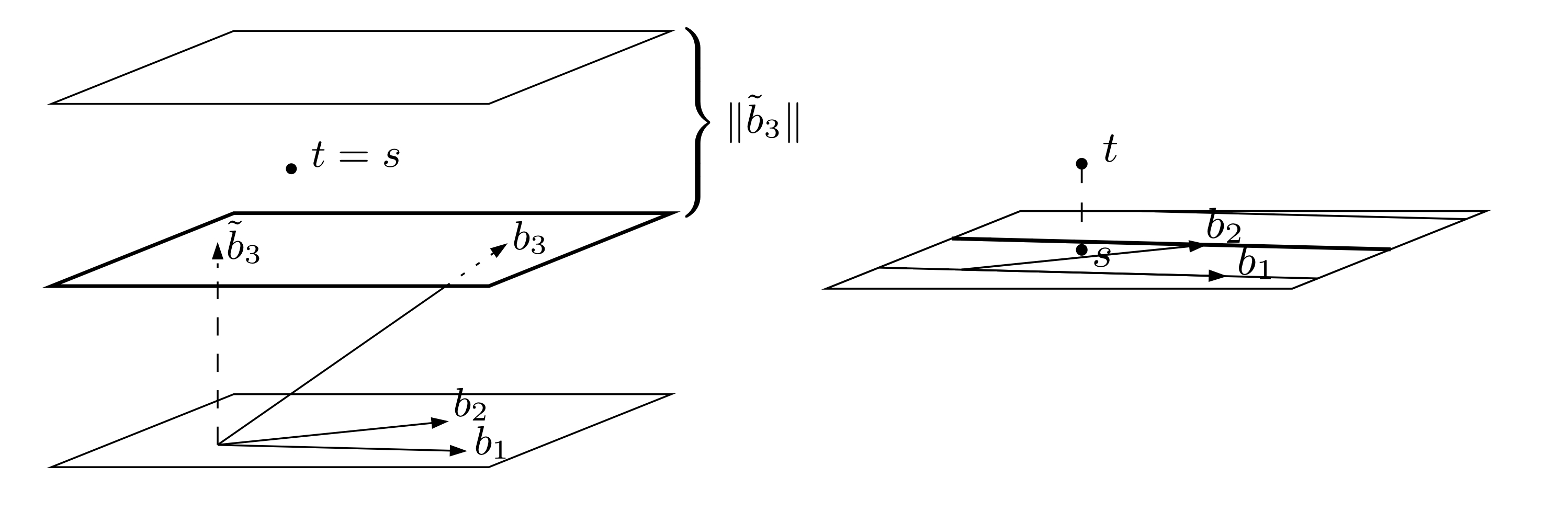
格密码中有一个原语叫做multilinear map，常应用于code obfuscation，这个领域出现了非常多新设计的困难问题。但这些困难问题有一个致命的弱点，暂时不能实现最坏情况和一般情况的安全归约，所以不被一些密码学家承认。但这其实是一个常见的发展路径，早些年全同态依赖的困难问题也是特殊设计的，只是后来不断发展后可归约到标准的LWE/RLWE困难问题。所以，本文章尝试梳理格密码论文中常用

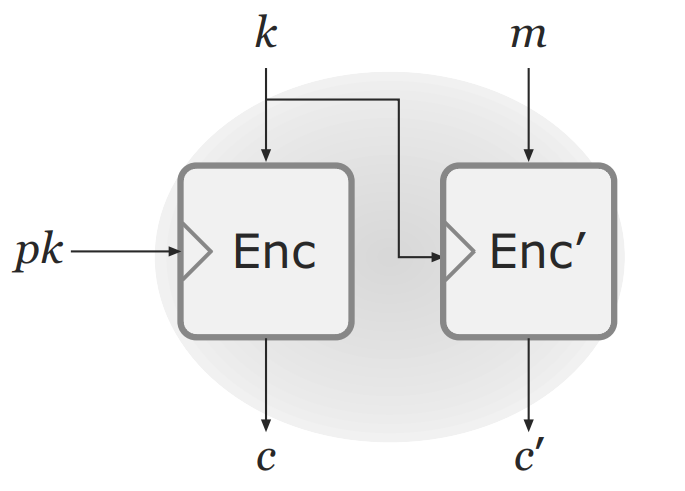
发送者调用Encaps算法来获得密文c以及密钥k。接着在私钥加密方案中，利用密钥k来加密明文m。

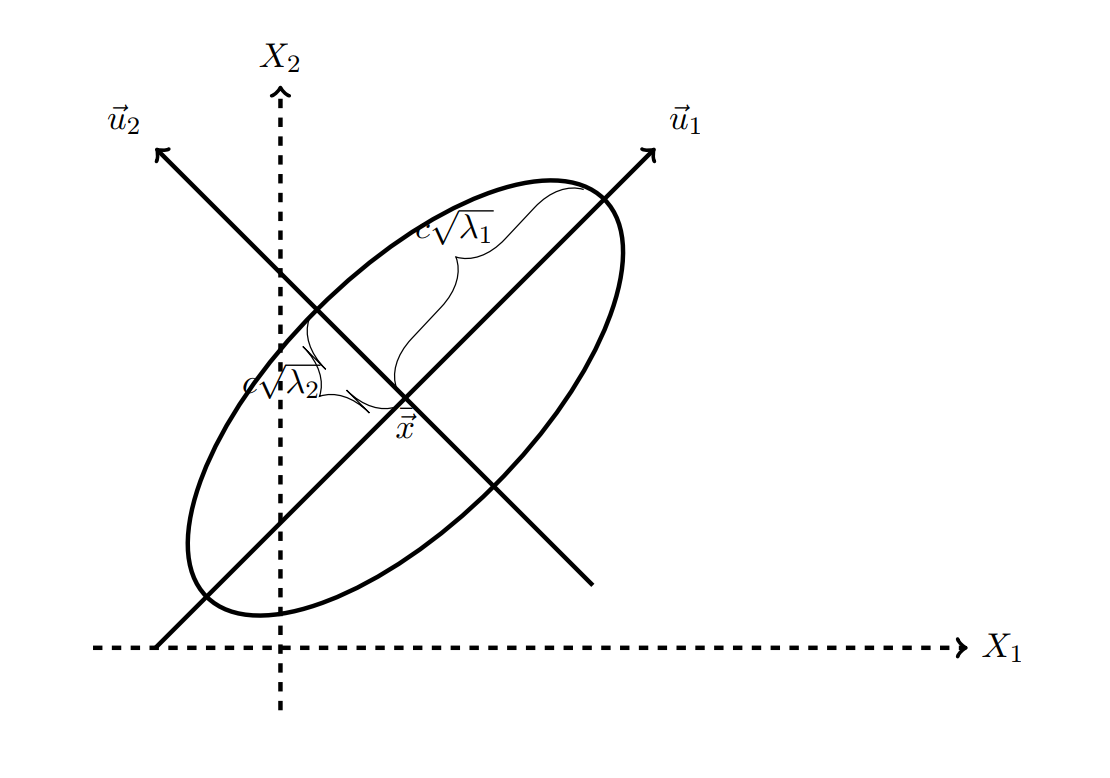
详解协方差矩阵，相关矩阵，互协方差矩阵（附完整例题分析）【1】-CSDN博客本篇文章主要关注相关矩阵以及例题分析。例题会总结这两篇文章的内容。

发射机将信息比特序列调制成PSK/QAM符号，然后对相应的符号执行IFFT(逆傅里叶变换）将其变换成时域信号，最后通过一个无线信道将它们发射出去。接收端信道估计的意义：接收的信号通常因受到信道特性的影响而失真。为了恢复发送的比特信息，在接收机必须对信道的影响进行估计和补偿；发射端信道估计的意义：设计预编码矩阵，避免自干扰；