🔥个人主页：@草莓熊Lotso

🎬作者简介：C++研发方向学习者

📖个人专栏： 《C语言》 《数据结构与算法》《C语言刷题集》《Leetcode刷题指南》

⭐️人生格言：生活是默默的坚持，毅力是永久的享受。

前言：今天这篇文章主要是想给大家分享一下计数排序，并且对前面实现过的排序算法的时间复杂度，空间复杂度，稳定性进行一个归纳总结。话不多说，我们直接进入正文内容。

---

目录

一.计数排序

核心步骤：

代码实现：

计数排序的特性： 

 二.排序算法复杂度及稳定性分析

各排序算法对比表： 

---

一.计数排序

计数排序（Counting Sort）又称为鸽巢原理，是一种非比较型的线性时间排序算法，适用于 输入数据范围明确且较窄的场景。核心思想是通过“统计每个值的出现次数”，直接确定元素的最终位置，跳过耗时的比较操作。

核心步骤：

1. 确定数据范围
遍历数组，找到最大值 max 和最小值 min，计算数据范围 range = max - min + 1。
（目的：创建合适大小的计数数组，避免空间浪费）

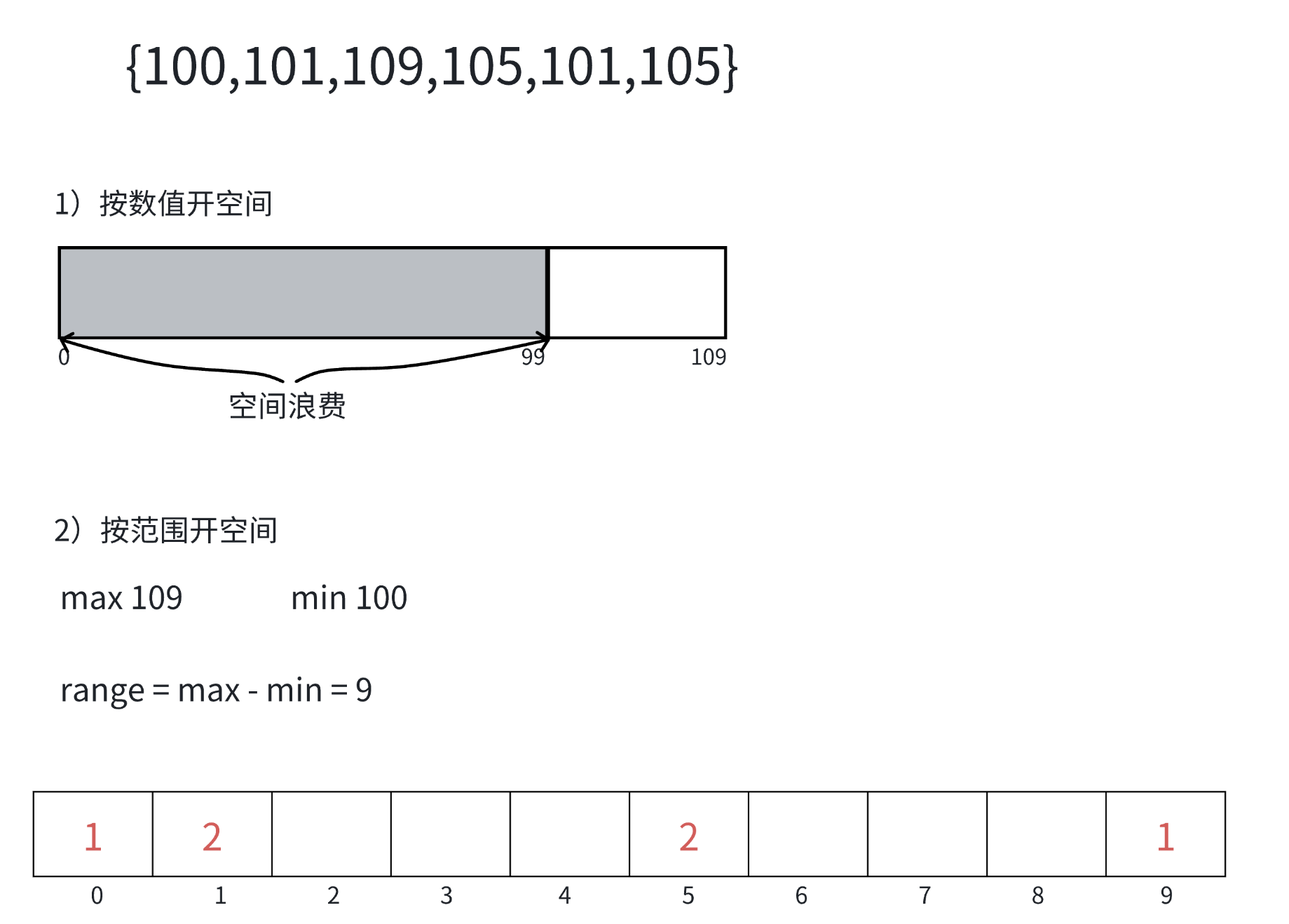
2. 统计元素出现次数
创建计数数组 count（长度为 range），注意count数组的初始化(开辟时用calloc或者后续用memset)，遍历原数组，将每个元素 arr[i] 映射到 count[arr[i] - min]（减去 min 是为了处理包含负数的情况，一定要用arr[i]-min），统计每个值的出现次数。

3. 将count数组中的数据排序还原到原数组中

定义一个索引变量index，用于记录原数组arr中即将写入数据的位置。遍历count数组(从0开始，然后小于<range)，根据count[i]统计到的个数进行循环，循环次数等于该值出现的次数，将数组的原始数据值放入arr原始数组中(对应原始值一定是i+min)

代码实现：

//非比较排序--计数排序
void CountSort(int* arr, int n)
{
	//找最大最小值确定范围
	int min = arr[0]; int max = arr[0];
	for (int i = 0; i < n; i++)
	{
		if (arr[i] < min)
		{
			min = arr[i];
		}
		if (arr[i] > max)
		{
			max = arr[i];
		}
	}

	int range = max - min + 1;
	int* count = (int*)malloc(sizeof(int) * range);
	if (count == NULL)
	{
		perror("malloc fail!");
		exit(-1);
	}

	//对count初始化，可以用memset也可以前面申请空间的时候使用calloc
	memset(count, 0, sizeof(int) * range);

	//统计次数，映射，下标为arr[i]-min
	for (int i = 0; i < n; i++)
	{
		count[arr[i] - min]++;
	}

	//排序
	int index = 0;
	//用range就可以了
	for (int i = 0; i < range; i++)
	{
		while (count[i]--)
		{
			arr[index++] = i + min;//这里需要用i+min
		}
	}
}

test.c：

#include"Sort.h"

void PrintArr(int* arr, int n)
{
	for (int i = 0; i < n; i++)
	{
		printf("%d ", arr[i]);
	}
	printf("\n");
}

void test1()
{
	int a[] = { 5, 3, 9, 6, 2, 4, 7, 1, 8 };
	int size = sizeof(a) / sizeof(a[0]);
	printf("排序前:");
	PrintArr(a, size);

	//直接插入排序
	//InsertSort(a, size);
	//希尔排序
	//ShellSort(a, size);
	//直接选择排序
	//SelectSort(a, size);
	//堆排序
	//HeapSort(a, size);
	//冒泡排序
	//BubbleSort(a, size);
	//快速排序
	//QuickSort(a, 0, size - 1);
	//非递归快速排序
	//QuickSortNoare(a, 0, size - 1);
	//快速排序进阶版
	//QuickSortMore(a, 0, size - 1);
	//归并排序
	//MergeSort(a, size);
	//非递归实现归并排序
	//MergeSortNore(a, size);

	//非比较排序--计数排序
	CountSort(a, size);

	printf("排序后:");
	PrintArr(a, size);
}


int main()
{
	test1();
	return 0;
}

--测试完成，打印没有问题，升序排序正确，退出码为0 

计数排序的特性： 

• 计数排序在数据范围集中时，效率很高，但是适用范围以及场景有限。
• 时间复杂度：O(n+range)
• 空间复杂度：O(range)
• 稳定性：稳定

---

 二.排序算法复杂度及稳定性分析

稳定性：假定在待排序的记录序列中，存在多个具有相同的关键字的记录，若经过排序，这些记录的相对次序保持不变，即在原序列中，r[i]=r[j]，且r[i]在r[j]之前，而在排序后的序列中，r[i]仍在r[j]之前，则称这种排序算法是稳定的；否则称为不稳定的。

各排序算法对比表： 

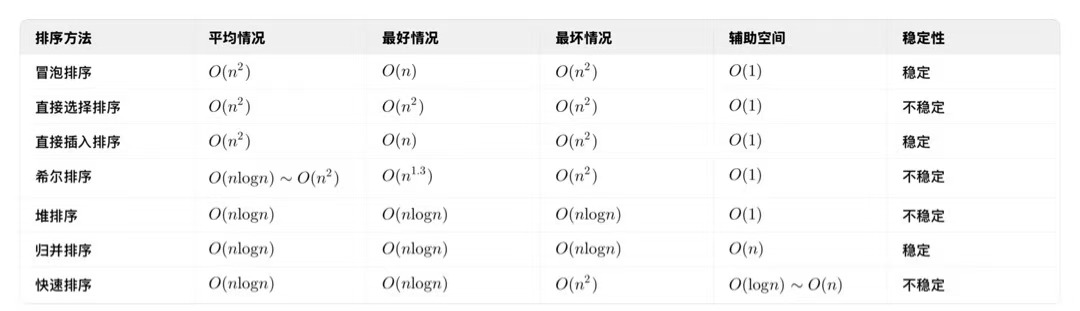
--其中冒泡排序，直接插入排序，归并排序是稳定的，这里就不过多介绍了，我们主要通过一些特例来看下那些不稳定的排序算法。至于时间复杂度和空间复杂度，博主大部分都在前面的博客中分享过了。

1.直接选择排序：

2.希尔排序：

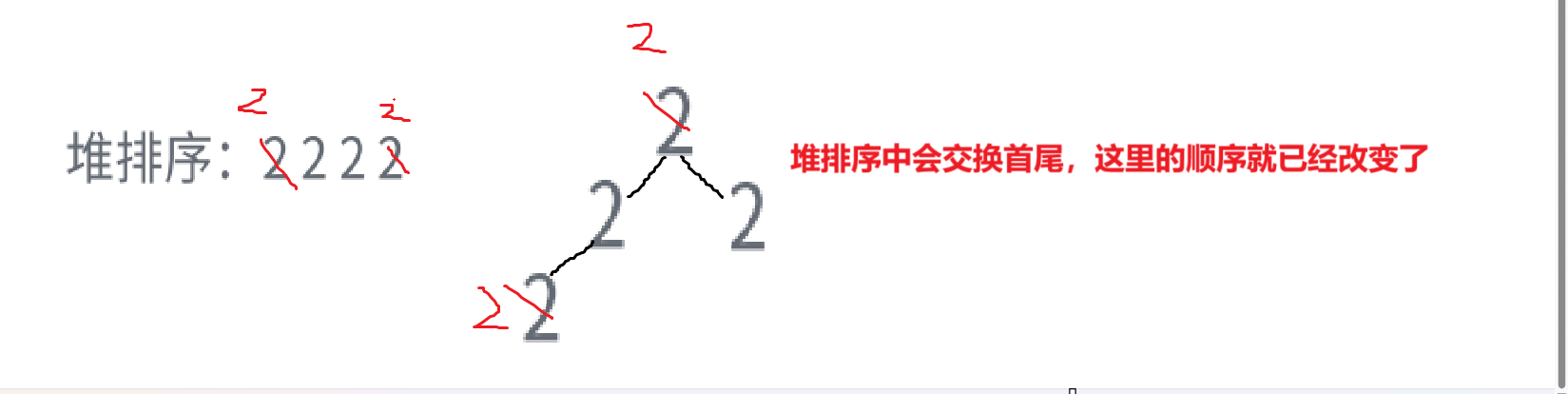
3.堆排序：

4.快速排序：

--前面一直没给大家展示过Sort.h文件，在这里给大家看一看

#pragma once
#include<stdio.h>
#include<stdlib.h>
#include<string.h>

//插入排序
//1)直接插入排序
void InsertSort(int* arr, int n);
//2)希尔排序
void ShellSort(int* arr, int n);

//选择排序
//1)直接选择排序
void SelectSort(int* arr, int n);
//2)堆排序
void HeapSort(int* arr, int n);

//交换排序
//1)冒泡排序
void BubbleSort(int* arr, int n);
//2)快速排序
void QuickSort(int* arr, int left, int right);
//快速排序非递归版本
void QuickSortNoare(int* arr, int left, int right);
//快速排序进阶版本
void QuickSortMore(int* arr, int left, int right);


//归并排序--主函数里面不递归，所以可以先不传left和right
void MergeSort(int* arr, int n);
//非递归实现归并排序
void MergeSortNore(int* arr, int n);


//非比较排序--计数排序
void CountSort(int* arr, int n);

---

往期回顾：

【数据结构初阶】--排序(一)：直接插入排序，希尔排序

【数据结构初阶】--排序(二)--直接选择排序，堆排序

【数据结构初阶】--排序(三)：冒泡排序，快速排序

【数据结构初阶】--排序(四)：归并排序

结语：本篇博客就到此结束了，后续应该还会更新一篇归并排序的进阶，然后就正式进入C++的学习了。我们数据结构初阶讲这些数据结构都是用C语言实现的，还有些比较难的数据结构在后续C++的学习中我们也会接触到，但是利用C++来实现就方便很多了，如果文章对你有帮助的话，欢迎评论，点赞，收藏加关注，感谢大家的支持。