目录

一、题目描述

二、算法原理

动态规划

1.前缀和

1.1同类累积

1.2所有路出

三、提交代码

---

一、题目描述

【模板】前缀和_牛客题霸_牛客网

描述

对于给定的长度为 nn 的数组 {a1,a2,…,an}{a1​,a2​,…,an​} ，我们有 mm 次查询操作，每一次操作给出两个参数 l,rl,r ，你需要输出数组中第 ll 到第 rr 个元素之和，即 al+al+1+⋯+aral​+al+1​+⋯+ar​ 。

输入描述：

第一行输入两个整数 n,m(1≦n,m≦105)n,m(1≦n,m≦105) 代表数组中的元素数量、查询次数。

第二行输入 nn 个整数 a1,a2,…,an(−109≦ai≦109)a1​,a2​,…,an​(−109≦ai​≦109) 代表初始数组。

此后 mm 行，每行输入两个整数 l,r(1≦l≦r≦n)l,r(1≦l≦r≦n) 代表一次查询。

输出描述：

对于每一次查询操作，在一行上输出一个整数，代表区间和。

示例

输入：

3 2
1 2 4
1 2
2 3

输出：

3
6

---

二、算法原理

动态规划

同类累积问题 可 所有路出

1.前缀和

1.1同类累积

前缀区间和 = 再前缀区间和 + 当前数（dp[i] = dp[i - 1] + arr[i]）

1.1.1拆拼

整体 拆成 能同类累积部分 拼合成：

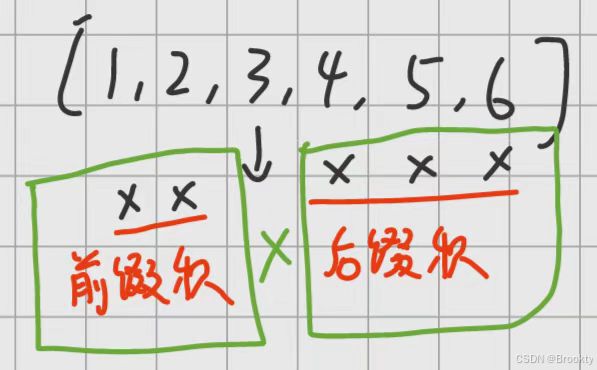
238. 除自身以外数组的乘积 - 力扣（LeetCode）

给你一个整数数组 nums，返回 数组 answer ，其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。

题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在  32 位 整数范围内。

请 不要使用除法，且在 O(n) 时间复杂度内完成此题。

示例 1:

输入: nums = [1,2,3,4]

输出: [24,12,8,6]

示例 2:

输入: nums = [-1,1,0,-3,3]
输出: [0,0,9,0,0]

提示：

• 2 <= nums.length <= 105
• -30 <= nums[i] <= 30
• 输入 保证 数组 answer[i] 在  32 位 整数范围内

public int[] productExceptSelf(int[] nums) {
    int n = nums.length;
    int[] f = new int[n], g = new int[n], ret = new int[n];
    f[0] = g[n - 1] = 1; // 直接维护 不含此元素 往前的前缀积的
    for (int i = 1; i < n; i++)
        f[i] = f[i - 1] * nums[i - 1];
    for (int i = n - 2; i >= 0; i--)
        g[i] = g[i + 1] * nums[i + 1];
    for (int i = 0; i < n; i++)
        ret[i] = f[i] * g[i];
    return ret;
}

---

1.2所有路出

所有前缀区间和 能 一路累积算出

---

三、提交代码

public static void main(String[] args) {
    Scanner in = new Scanner(System.in);
    int n = in.nextInt(), m = in.nextInt();
    int[] array = new int[n + 1];
    for(int i = 1;i <= n;i++) array[i] = in.nextInt();

    // 所有前缀和累积算出
    long[] dp = new long[n + 1];
    for(int i = 1;i <= n;i++) dp[i] = dp[i - 1] + array[i];

    while(m > 0) {
        int l = in.nextInt(), r = in.nextInt();
        System.out.println(dp[r] - dp[l - 1]);
        m--;
    }
}