深入浅出概率扩散模型(DDPM):从马尔科夫链到公式推导
今天我们来学习一个在人工智能绘画和生成模型领域非常火热的模型——概率扩散模型(Probabilistic Diffusion Model, DDM)。
今天我们来学习一个在人工智能绘画和生成模型领域非常火热的模型——概率扩散模型(Probabilistic Diffusion Model, DDM)。
在学习扩散模型之前我们先学习一下马尔科夫链,这对于扩散模型的学习是很有帮助的,我会尽量用直观简单的方法带大家学会马尔科夫链
第一章:马尔科夫链的基本原理
马尔可夫链是理解很多随机过程(包括我们之前讲的扩散模型)的基础,它的核心思想其实非常简单和直观。
一句话概括就是:未来只与现在有关,与过去无关。
这也被称为“无记忆性”或“马尔可夫性质”。
下一步的状态,只依赖于当前状态,而不依赖于过去更早的历史。
换句话说:
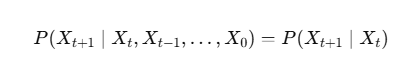
所以你可以把它想成:
“每次往前走一步”,
“走哪一步的概率,只取决于你现在的位置”,
“你是怎么来到这里的不重要”。
举例
有一个老年痴呆患者,名叫小忘,记性不太好。他每天只会在三个地方散步:【公园】、【商场】、【图书馆】。
小忘有一个固定的行为模式,他下一步去哪里,只取决于他现在在哪里,而完全不记得他之前去过哪些地方。
比如,他的行为概率是这样的:
如果小忘现在在【公园】:
-
他有 10% 的概率明天还待在【公园】。
-
他有 60% 的概率明天会去【商场】。
-
他有 30% 的概率明天会去【图书馆】。
如果小忘现在在【商场】:
-
他有 40% 的概率明天会去【公园】。
-
他有 20% 的概率明天还待在【商场】。
-
他有 40% 的概率明天会去【图书馆】。
如果小忘现在在【图书馆】:
-
他有 80% 的概率明天会去【公园】。
-
他有 10% 的概率明天会去【商场】。
-
他有 10% 的概率明天还待在【图书馆】。
看到了吗?要预测小忘明天去哪,我们只需要知道他今天在哪就行了。至于他昨天、前天是在公园还是商场,对明天的决定毫无影响。他是个“活在当下”的机器人。
这个描述小忘散步的系统,就是一个马尔可夫链。
马尔可夫链的三个核心要素
-
状态(States):系统可能存在的几种情况。在小忘的例子里,状态就是三个地点:
{公园, 商场, 图书馆}。 -
转移(Transitions):从一个状态移动到另一个状态的过程。比如,小忘从【公园】走到【商场】。
-
转移概率(Transition Probabilities):从当前状态转移到下一个状态的概率。例如,从【公园】转移到【商场】的概率是 60%(或 0.6)。
我们可以用一个 转移矩阵 来清晰地表示所有这些概率:
| 明天去公园 | 明天去商场 | 明天去图书馆 | |
| 今天在公园 | 0.1 | 0.6 | 0.3 |
| 今天在商场 | 0.4 | 0.2 | 0.4 |
| 今天在图书馆 | 0.8 | 0.1 | 0.1 |
| (注意:每一行的概率加起来必须等于 1,因为小忘明天必须去一个地方) |
规定好行和列的顺序:
-
行 (Rows) 代表 出发点(当前状态)
-
列 (Columns) 代表 目的地(下一个状态)
转移矩阵的强大之处:预测未来
它不仅能告诉我们“下一步”的概率,还能帮我们计算“下两步”、“下N步”**的概率。
怎么做呢?通过矩阵的乘法
-
两步之后的转移概率:计算 P² = P × P (矩阵P乘以它自己)。得到的新矩阵就会告诉你,从任意地点出发,经过两步之后,到达各个地点的概率是多少。
-
N 步之后的转移概率: 计算 Pⁿ。
举个例子: 假设小忘今天在【公园】,我想知道后天(也就是两步之后)他会在【图书馆】的概率是多少?
我需要计算 P² 矩阵中,第一行(代表从公园出发)第三列(代表到图书馆结束)的那个数字。
这个计算过程虽然有点繁琐,但计算机可以瞬间完成。它揭示了马尔可夫链的长期行为趋势。
再来个简单的例子,便于我们计算:
状态集合:{晴(S), 雨(R)}
假设规则:
-
如果今天晴,明天 70% 还是晴,30% 下雨。
-
如果今天雨,明天 40% 放晴,60% 继续下雨。
那么转移矩阵 P是:
解释:
-
第一行 (当前=晴):
-
转到晴的概率 0.7
-
转到雨的概率 0.3
-
-
第二行 (当前=雨):
-
转到晴的概率 0.4
-
转到雨的概率 0.6
-
如果知道今天的分布 ,比如今天 100% 晴天:
π0=[1,0]
那么明天的分布是:
意思是:明天有 70% 概率晴,30% 概率雨。
后天(两步后)分布是:
= [0.61,0.39]
第 3 天: = [0.583,0.417]
第 4 天: =[0.5749,0.4251]
可以看见最后在靠近一个固定数值,这个固定数值就是极限稳态分布:
π∗=[7/4,7/3]≈[0.5714,0.4286]。
可以看到 π2,π3,π4 正在向它靠近。
它的直观意义
-
你可以把马尔可夫链看作“随机游走”。
-
经过足够多步之后,它“忘记”了自己最初是从哪里出发的。
-
最终,它会停留在某种 长期平均的比例 上。
换句话说,极限稳定分布:
如果你随机长期观察这个系统,每个状态出现的频率是多少。
马尔科夫链就讲到这里,如果需要更深入的讲解,请在下方留言,我会更新
第二章:扩散模型原理讲解与数学推导
第一课:核心思想 —— 从“混沌”中创造“有序”
想象一下,你手上有一张清晰的猫的图片。
1.加噪过程(Forward Process / Diffusion Process): 现在,我们开始对这张图片做一件“破坏性”的事情:给它撒上一点点微小的、随机的“噪声”(就像电视雪花点一样)。只加一点点,图片看起来变化不大。 然后,我们再重复这个过程,在已经有点模糊的图片上再加一点点噪声。 …… 不断重复成百上千次后,你最终会得到什么?没错,一张看起来完全是随机噪声、毫无规律的图片,原来的猫咪已经完全看不见了。
这个从清晰图片逐渐变为纯噪声的过程,我们称之为“前向过程”或“扩散过程”。这个过程是固定的、可控的,因为我们知道每一步加了多少噪声。从数学上讲,我们是在逐步将一个复杂的数据分布(猫的图片)变成一个简单的、已知的概率分布(高斯噪声分布)。
2.去噪过程(Reverse Process / Denoising Process): 好了,现在是见证奇迹的时刻。扩散模型最神奇的地方在于,它学会了如何“逆转”上面那个过程。 我们给模型一张纯粹由随机噪声构成的图片,然后对它说:“这张噪声图片,是我对一张真实的猫咪图片加了1000次噪声后得到的,请你帮我还原它。” 模型就会开始它的工作:
第一步: 它会尝试预测并去除“最后一次”加入的噪声,得到一张稍微不那么“混沌”的图片。
第二步: 在新图片的基础上,它继续预测并去除“倒数第二次”加入的噪声。
……
第一千步: 当它重复这个过程1000次后,一张清晰的、全新的、由AI创造的猫咪图片就诞生了!
这个从纯噪声逐渐恢复到清晰图片的过程,我们称之为“反向过程”或“去噪过程”。这就是AI进行“创作”的过程。
小结一下核心思想: 扩散模型通过一个“先破坏再重建”的过程来学习。它首先学习如何系统地、逐步地破坏一张图片(前向过程),然后学会如何从无到有、一步步地逆转这个破坏过程(反向过程),从而创造出新的图片。
第二课:深入—— 数学原理
现在我们稍微深入一些,看看背后的数学原理。别怕,我会讲得很直观。
第一部分:前向过程 (Forward Process) —— “破坏”的数学
这个过程是我们预先定义好的,它的任务是把清晰图片 x0 变成纯噪声 xT。
公式 1:单步加噪 (Step-by-step Noising)
这是描述如何从上一步图片 xt−1 得到当前图片 xt 的规则。
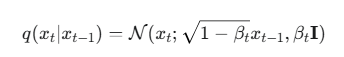
公式解读:
![]() :这是一个条件概率,读作“在给定 xt−1 的条件下, xt 的概率分布”。
:这是一个条件概率,读作“在给定 xt−1 的条件下, xt 的概率分布”。
![]() :这代表高斯分布(正态分布)。高斯分布由两样东西决定:
:这代表高斯分布(正态分布)。高斯分布由两样东西决定:
-
均值 (Mean) μ:分布的中心位置,可以理解为“最期望得到的值”。
-
方差 (Variance) σ^2:分布的胖瘦程度,代表数据围绕均值的分散程度,可以理解为“不确定性”或“噪声强度”。
在我们的公式里:
![]() :
:
x_t−1 是上一时刻的图片。
β_t 是一个我们提前设定的、非常小的正数(例如0.0001到0.02),它代表在第 t 步加入噪声的“量”。
![]() :是一个略小于1的数。所以,这一项的意思是把上一张图片 xt−1 的像素值整体稍微缩小一点点,让它变暗一些。
:是一个略小于1的数。所以,这一项的意思是把上一张图片 xt−1 的像素值整体稍微缩小一点点,让它变暗一些。
![]() :这代表我们要加入的高斯噪声的强度。强度就由我们设定的 βt 来控制。
:这代表我们要加入的高斯噪声的强度。强度就由我们设定的 βt 来控制。
I 是单位矩阵,意思是给每个像素独立地加入噪声。
一句话白话文: “xt 这张图片,是通过把 xt−1 稍微调暗一点,然后叠加上一层强度为 βt 的随机噪声得到的。”
公式 2:一步直达 (The "Magic" Formula for Training)
上节课我们得到了这个单步加噪声公式:
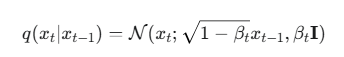
![]()

对于:![]() :
:
βt∈(0,1) 是第 t 步加的噪声强度
αt=1−βt 是“保留多少原信号”;
![]() :是从第 1 到第 t 步累计保留的“总信号比例”
:是从第 1 到第 t 步累计保留的“总信号比例”
在说啥
步数越大, 越小 → 原信号越淡,噪声越多。
为什么这样
逐步把复杂数据磨成高斯噪声(最后很容易采样),方便做“从噪声到数据”的逆过程。
现在来看公式的组成:
x0:最原始的、清晰的图片。
ϵ:一个全新的、从标准高斯分布中随机采样的噪声图。
![]() :随着 t 变大,αˉt 会越来越小。所以这一项代表,在 xt 中,原始图片 x0 的“残存信息”。t 越大,残存信息越少。
:随着 t 变大,αˉt 会越来越小。所以这一项代表,在 xt 中,原始图片 x0 的“残存信息”。t 越大,残存信息越少。
![]() 随着 t 变大,1−αˉt 会越来越接近1。所以这一项代表,在 xt 中,随机噪声 ϵ 所占的“比重”。t 越大,噪声比重越大。
随着 t 变大,1−αˉt 会越来越接近1。所以这一项代表,在 xt 中,随机噪声 ϵ 所占的“比重”。t 越大,噪声比重越大。
一句话白话文:
“第 t 步的噪声图片 xt ,可以看作是按![]() 比例缩放的原始图片,和按
比例缩放的原始图片,和按![]() 比例缩放的随机噪声,两者混合而成的。
比例缩放的随机噪声,两者混合而成的。
这个公式是训练的关键,因为它让我们可以在训练时随机跳到任何 t 时刻,极大提高了效率。
第二部分:反向过程 (Reverse Process / Denoising Process)
这是整个模型最关键、最神奇,也是唯一需要学习的部分。
我们的目标是,从一张纯噪声图片 xT 开始,一步步地把噪声去掉,逆转上面的过程,最终恢复出原始图片 x0。
也就是说,我们想要知道![]() 是什么样的。如果我们能模拟这个分布,就能从 xt 推导出 xt−1,然后一步步推回到 x0。
是什么样的。如果我们能模拟这个分布,就能从 xt 推导出 xt−1,然后一步步推回到 x0。
但是,直接计算![]() 非常困难,因为它需要用到整个数据集的信息。所以,我们用一个神经网络来近似这个分布。我们把这个神经网络定义的分布记为
非常困难,因为它需要用到整个数据集的信息。所以,我们用一个神经网络来近似这个分布。我们把这个神经网络定义的分布记为![]()
其中 θ 是神经网络的参数。
我们假设这个反向过程也是一个高斯过程:
![]()
公式解读:
我们的神经网络需要做的事情就是:输入当前的噪声图片 xt 和当前的时间步 t,然后预测出这个分布的均值:![]() 与方差:
与方差:![]()
在实践中,研究者发现,将方差![]() 固定为一个常数(比如 βtI)效果也很好
固定为一个常数(比如 βtI)效果也很好
所以,模型的核心任务就变成了只预测均值:![]()
如何训练这个神经网络?
回忆一下前向过程的公式:
![]() 我们可以把它变一下形:
我们可以把它变一下形:
![]()
通过贝叶斯定理和一些数学推导(这里我们省略复杂的步骤)
可以证明,我们想要预测的那个均值 μθ(xt,t) 和添加到 xt 中的噪声 ϵ 有着直接的线性关系。
最终,人们发现,与其让神经网络直接预测均值 μθ,不如让它来预测在第 t 步添加的噪声 ϵ。这在实践中被证明效果更好、更稳定。
所以,我们的神经网络模型,通常用 ϵθ(xt,t) 来表示,它的任务就是:
输入一张加了噪的图片 xt 和时间步 t,输出一个预测的噪声 ϵθ。
第三部分:训练目标 (Training Objective)
我们如何让神经网络预测的噪声 ϵθ 和当时我们真正加进去的噪声 ϵ 尽可能地接近呢?最简单的方法就是让它们的均方误差(Mean Squared Error, MSE)最小。
所以,扩散模型的损失函数(Loss Function)可以简化为:

![]() :表示我们对所有可能的情况求一个期望(平均值)。
:表示我们对所有可能的情况求一个期望(平均值)。
训练步骤:
-
从我们的数据集中随机抽取一张清晰的图片 x0。
-
随机选择一个时间步 t(从 1 到 T)。
-
生成一个随机的高斯噪声 ϵ。
-
根据公式计算
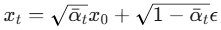 出加噪后的图片 xt
出加噪后的图片 xt -
将 xt 和 t 输入到我们的神经网络 ϵθ 中,得到预测的噪声 ϵθ(xt,t)
-
计算真实噪声 ϵ 和预测噪声 ϵθ 之间的差距(L2 范数的平方,也就是 MSE)
-
根据这个差距,使用梯度下降等优化算法来更新神经网络的参数 θ,目标是让这个差距越来越小。
我们不断重复这个过程,神经网络 ϵθ 就会变得越来越擅长“猜”出图片中包含了什么样的噪声。
第四部分:生成/采样 (Sampling)
当模型训练好之后,我们就可以用它来生成全新的图片了!
1.起始:我们从一个完全随机的噪声图片 xT 开始,这个噪声是从标准高斯分布 N(0,I) 中采样得到的。
2.迭代降噪:我们从最后一个时间步 T 开始,一步步往前推,直到 t=1。
在每一步 t,我们将当前的图片 xt 和时间步 t 输入到我们训练好的神经网络 ϵθ(xt,t),得到预测的噪声。
使用这个预测的噪声,通过一个特定的采样公式(例如 DDPM 的采样公式)来计算出上一步的图片 xt−1。
一个常用的采样公式是:

其中 z 是一个新的随机噪声,σt 是一个控制随机性的系数。
3.最终结果:当这个迭代过程进行到最后一步,我们得到的 x0 就是一张由模型生成的、全新的、清晰的图片。
总结
好了,我们来回顾一下整个流程:
-
前向过程(固定):x0→x1→⋯→xT (图片 → 噪声)
-
通过逐步添加高斯噪声,将一张清晰图片变成纯噪声。
-
这个过程的数学公式是固定的,不需要学习。
-
-
反向过程(学习):xT→xT−1→⋯→x0 (噪声 → 图片)
-
训练一个神经网络 ϵθ,让它学会预测每一步中添加的噪声。
-
训练的目标是让预测的噪声和真实的噪声之间的均方误差最小。
-
-
采样(生成):
-
从一个随机噪声 xT 出发。
-
利用训练好的神经网络,一步步地执行降噪过程,最终生成一张清晰的图片 x0。
-
扩散模型之所以强大,是因为它将一个非常困难的“一步生成”问题,分解成了很多个非常简单的“去掉一点点噪声”的小问题,然后通过一个强大的神经网络(通常是 U-Net 结构)来解决这些小问题。
实例讲解:
我们来把这个过程“可视化”,不过我们不用一张复杂的图片,而是用一个最简单的数据:只有一个像素的灰度图片。
假设这个像素的值在 -1 到 1 之间(-1 是纯黑,1 是纯白)。
实例设定:
原始数据 (x0): 我们的“清晰图片”就是一个像素,值为 [0.8] (一个亮灰色像素)。
总时间步 (T): 我们把加噪过程缩短到 T=3 步,方便观察。
噪声计划 (βt): 我们设定一个简单的、递增的噪声计划:
-
β1=0.1
-
β2=0.3
-
β3=0.5
派生参数 (αt,αˉt): 根据公式我们可以计算出:
-
α1=1−β1=0.9
-
α2=1−β2=0.7
-
α3=1−β3=0.5
-
αˉ1=α1=0.9
-
αˉ2=α1×α2=0.9×0.7=0.63
-
αˉ3=αˉ2×α3=0.63×0.5=0.315
第一步:前向过程(加噪声,“破坏”)
我们从 x0=[0.8] 开始,看看它如何一步步变成噪声。我们会使用便捷公式
![]()
在 t=1 时:
1.我们需要一个随机噪声 ϵ1,假设我们随机采样的结果是 ϵ1=[0.2]。
2.计算 x1:
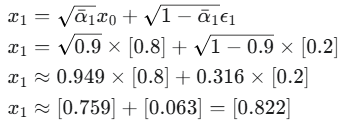
结果:像素值从 [0.8] 轻微晃动到了 [0.822]。
在 t=2 时:
1、我们需要一个新的随机噪声 ϵ2,假设是 ϵ2=[−0.5]。
2.
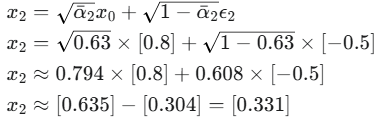
结果:像素值已经变得更模糊,离原始值更远了。
在 t=3 时:
1.再来一个随机噪声 ϵ3,假设是 ϵ3=[0.9]。

结果:像素值变得非常随机,几乎看不出和原始值 [0.8] 的关系。如果 T=1000,那 xT 就是一个纯粹的随机值了。
第二步:反向过程(训练模型)
现在,我们有了“破坏”过程的样本,该训练我们的神经网络 ϵθ(xt,t) 了。
一个训练样本的诞生:
我们从上面的过程中随便挑一个,比如 t=2 的那次计算。
模型的输入 (Input): 噪声图片 x2=[0.331] 和时间步 t=2。
模型需要预测的目标 (Target): 当时我们加入的噪声 ϵ2=[−0.5]。
训练循环中的一步:
1、我们将 [0.331] 和 t=2 送入神经网络 ϵθ。
2、网络进行预测,由于它还没训练好,可能会给出一个完全不准的预测值,比如 ϵθ(x2,2)=[0.4]。
3、我们计算损失 (Loss),也就是预测和目标之间的差距:
![]()
4、这个损失值 0.81 会告诉我们,模型的预测“错得有多离谱”。然后,通过反向传播算法,微调神经网络内部的参数,让它下一次再遇到类似 [0.331] 这样的输入时,输出能更接近 [-0.5] 一点。
这个过程会重复亿万次,用上我们所有的数据(成千上万张真实图片)和所有的时间步 t,最终,神经网络 ϵθ 会变得非常擅长“看山不是山”,即看到一张噪声图,就能准确地猜出里面的噪声是什么。
第三步:生成过程(从无到有,“修复”)
假设我们的模型已经训练好了。现在我们来生成一个全新的像素。
从 t=3 (纯噪声) 开始:
1.我们先随机生成一个高斯噪声作为起点:x3=[1.194] (为了方便对比,我们用前向过程的最终结果,但实际生成时是完全随机的)。
2.将 x3 和 t=3 送入我们训练好的模型 ϵθ。因为它训练得很好,它的预测会非常接近我们当时加入的噪声 ϵ3:
![]()
3.使用采样公式计算 x2:
![]()
![]()
你看,我们从一个很随机的值 [1.194] 降噪后,得到了一个更“温和”的值 [0.920]。
从 t=2 到 t=1:
1.将得到的 x2=[0.920] 和 t=2 送入模型。
2.模型预测出噪声:
3.用采样公式计算 x1:
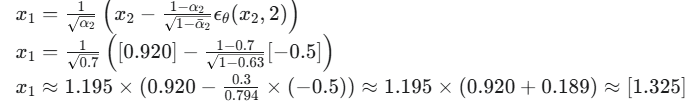
这个结果可能看起来有点奇怪,但这是因为我们的T太小,每一步变化很大。在T=1000的真实模型里,这个过程会平滑得多。
从 t=1 到 t=0 (最后一步):
1.将 x1=[1.325] 和 t=1 送入模型。
2.模型预测出噪声:ϵθ(x1,1)≈[0.2]
3.计算最终的 x0:

最终生成结果:x0=[1.33]。
虽然这个值不等于我们最开始的 [0.8],但它是一个由模型从纯噪声中“创造”出来的、合理的、清晰的像素值。如果我们的训练数据里有很多 [0.8] 这样的亮灰色像素,那么模型从随机噪声开始,最后就很可能生成一个接近 [0.8] 的值。
这个例子虽然非常简化,但它完整地展示了扩散模型的每一步是如何进行数值计算的。现在,你可以想象一下,把这个单像素的操作,扩展到一个 512x512 的彩色图片上,原理是完全一样的
以上就是关于扩散模型的讲解了,有不懂的地方可以提出来,后续文章我继续讲解。
更多推荐
 已为社区贡献1条内容
已为社区贡献1条内容









所有评论(0)