Transformer Linear Attention

Attention计算时间复杂度

在之前的讨论中，我们探讨了如何通过稀疏化技术来减少自注意力机制的计算负担。除此之外，如果能够将计算复杂度从平方级别降低到线性级别，那么就能彻底解决随着输入长度增加而急剧上升的计算资源消耗问题。
我们之前提到，自注意力机制的经典挑战在于其计算公式： $$\text{Attention}(Q,K,V)=\text{softmax}\left(\frac{Q{K}^T}{\sqrt{d_{\text{model}}}}\right)V$$ 在这个公式中，由于 $Q$、$K$ 和 $V$ 矩阵的乘法操作有特定的顺序，导致自注意力机制的计算复杂度和内存使用量都与序列长度的平方成正比，即 $O(n^2)$，其中 $n$ 代表序列的长度。
由于 $Q$、$K$ 和 $V$ 都是 $n\times d$ 的实数矩阵，即 $Q,K,V\in {\mathbb{R}}^{n\times d}$，其中 $n$ 是序列长度，$d$ 是嵌入维度。

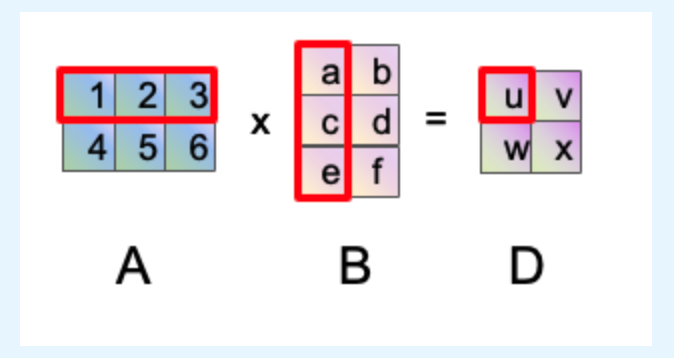
矩阵乘法时间复杂度

我们在计算两个矩阵乘法时，计算逻辑具体如下:

1. 首先我们取A矩阵的一行
2. 然后我们取B矩阵的一列
   

3. 最后把每一个对应位置的元素进行相乘相加，也就是$$u=1\ast a+2\ast c+3\ast e$$$$w=4\ast a+5\ast c+6\ast e$$ $$v=1\ast b+2\ast d+3\ast f$$ $$x=4\ast b+5\ast d+6\ast f$$
   上面的等式做个乘法就计数时间复杂度为1，比如计算$u$的结果，进行了3次乘法认为时间复杂度为3
   按照图中A矩阵维度是3*2，B矩阵维度是2*3，其计算的时间复杂度$3\ast 2^2$

因此对于一般的矩阵计算，矩阵A维度为($d_a$，$d$)，矩阵B维度为($d$，$d_b$)，（其中矩阵A、B相连的d维度要保持一致），其时间复杂度为$O(d_a\ast d\ast d_b)$

那么推导到Attention的计算公式中 $\text{softmax}\left(\frac{Q{K}^T}{\sqrt{d_{\text{model}}}}\right)V$
我们设定以下维度：

• 序列长度 (n): 4 (例如，一个包含4个词的句子)

• 特征维度 (d_k): 2 (每个词的嵌入向量是2维)
  现在，我们定义我们的查询（Q）、键（K）、值（V）矩阵：

• Q 的形状: [n, d_k] -> [4, 2]

• K 的形状: [n, d_k] -> [4, 2]

• V 的形状: [n, d_v] -> [4, 2]

我们给它们赋上具体的值以便计算：

Q = [[1, 2], [3, 4], [5, 6], [7, 8]]
K = [[1, 1], [1, 1], [1, 1], [1, 1]]
Kᵀ = [[1, 1, 1, 1], [1, 1, 1, 1]] #转置
V = [[1, 0], [0, 1], [1, 0], [0, 1]]

计算 QKᵀ 及其复杂度
QKᵀ计算时，Q矩阵维度($n$,$d_k$)，Kᵀ矩阵维度($d_k$,$n$)
复杂度分析：

• 输出矩阵有 n * n = 16 个元素。
• 计算输出矩阵中的每一个元素，都需要进行 d_k = 2 次乘法和 d_k-1 = 1 次加法（即 d_k 次点积操作）。
• 因此，总的计算次数（浮点运算次数，FLOPs）为 $n\ast n\ast d_k=4\ast 4\ast 2$ 。

推广到一般情况：

• 计算复杂度: O(n² * d_k)
  由于 d_k 是一个固定的常数（例如64，128），我们通常简化为 O(n²d)。
• 当序列长度 n 增加时（比如从处理一句话变为处理一篇文章），计算量会呈平方级增长。这就是为什么原始的Transformer模型在处理长文本时非常缓慢和耗费内存的原因。

计算 KᵀV 及其复杂度

KᵀV计算时，Kᵀ矩阵维度($d_k$,$n$)，V矩阵维度($n$,$d_k$)
复杂度分析：

• 输出矩阵有 d_k * d_v = 4 个元素。 (d_k = d_v = 2)
• 计算输出矩阵中的每一个元素，都需要进行 n = 4 次乘法和 n-1 = 3 次加法（即 n 次点积操作）。
• 因此，总的计算次数为 d_k * d_v * n。

推广到一般情况：

• 计算复杂度: O(d_k * d_v * n)
  由于 d_k 和 d_v 是固定常数，我们通常简化为 O(nd²)。

KᵀV 与 QKᵀ 矩阵计算时间复杂度

意义: 计算量只与序列长度 n 呈线性关系。无论序列有多长，只要 d 不变，KᵀV 的计算代价远小于 QKᵀ。
假设 n=1000, d=64：
* QKᵀ 的FLOPs ≈ 1000 * 1000 * 64 = 64,000,000
* KᵀV 的FLOPs ≈ 64 * 64 * 1000 = 4,096,000
前者是后者的 15 倍 以上。当 n=10000 时，前者将是后者的 150 倍 以上。

线性注意力的核心思想

线性注意力（Linear Attention）的关键在于改变注意力的计算顺序，避免显式计算 $Q{K}^T$。

在传统注意力中：
$$\text{Attention}=\text{softmax}(Q{K}^T)V$$
必须先计算 $Q{K}^T$（$O(n^{2}d)$），然后与 $V$ 相乘。根据上述的推导，计算量只与序列长度 n 呈线性关系。无论序列有多长，只要 d 不变，KᵀV 的计算代价远小于 QKᵀ。那么我们可以先计算 $K^{T}V$ 再与Q相乘这样能减少计算代价。
!!#ff6666 但是Attention公式中需要先做$softmax$，即$\text{softmax}(Q{K}^T)$，不能跳过$softmax$做 $K^{T}V$相乘，在线性注意力中!!，通过核函数（kernel function） 或特征映射（feature map），将注意力重写为：
$$\text{Attention}\approx \varphi (Q)(\varphi (K{)}^T\varphi (V))$$
其中 $\varphi$ 是一个将向量映射到非负空间的函数（如 softmax、elu+1 等）。

此时：

• $\varphi (K{)}^T\varphi (V)$ 是 $d\times d$ 矩阵，复杂度 $O(n{d}^2)$。
• $\varphi (Q)$ 是 $n\times d$，与 $d\times d$ 矩阵相乘，复杂度 $O(n{d}^2)$。
• 总复杂度为 $O(n{d}^2)$，关于 $n$ 是线性的。

总结

线性注意力是解决 Transformer 模型平方复杂度问题的一种重要且优雅的思路。它通过核技巧和改变计算顺序，将计算复杂度从 $O(n^2)$ 成功降低到 $O(n)$，突破了模型处理长序列的瓶颈。
尽管它在理论表达能力和实际性能上可能无法完全等同于标准注意力，但其在效率上的巨大提升使其在长序列建模领域具有不可替代的价值，是推动 Transformer 模型在更广阔领域应用的关键技术之一。