目录

数据结构查找：开启数字世界的寻宝之旅

一、查找的基石：基本概念大揭秘

（一）查找表：数据的有序集合

（二）关键字：数据的身份标识

（三）查找操作：目标数据的定位

（四）静态与动态查找表：数据的静态与动态管理

（五）平均查找长度：衡量查找效率的标尺

二、常见查找方法深度剖析

（一）顺序查找：简单直接的遍历查找

（二）折半查找：有序数据的高效查找

（三）分块查找：结合顺序与折半的查找策略

（四）二叉排序树查找：树形结构的查找优势

（五）散列表查找：基于哈希的快速查找

三、实战演练：数据结构查找的应用

（一）学生成绩管理系统中的查找应用

（二）图书管理系统中的书籍检索

（三）数据库索引中的查找技术

四、总结与展望：数据结构查找的未来之路

---

数据结构查找：开启数字世界的寻宝之旅

在生活里，我们常常会有这样的经历：走进一座大型图书馆，想要寻找一本心仪已久的书籍。此时，图书馆那一排排高大的书架上摆满了密密麻麻的书籍，让人有些眼花缭乱。但好在，我们可以借助图书馆的检索系统，在输入书籍的关键信息后，系统便能迅速定位到它所在的区域、书架和具体位置，从而帮助我们快速找到那本 “隐藏” 在书海之中的目标书籍。

这看似平常的找书过程，其实就蕴含着数据结构查找的基本思想。在计算机的世界里，数据就如同图书馆里的书籍，数量庞大且种类繁多。而数据结构查找，正是一种帮助计算机在海量数据中快速定位到所需信息的关键技术，它就像是图书馆检索系统，能够让计算机高效地找到目标数据 ，从而极大提升了数据处理和利用的效率。接下来，就让我们一同走进数据结构查找的世界，去揭开它神秘的面纱。

一、查找的基石：基本概念大揭秘

（一）查找表：数据的有序集合

查找表，是由同一类型的数据元素构成的集合，它就像是一个有序的 “数据仓库” ，将相关的数据有条理地存储起来，为后续的查找操作提供基础。就好比我们学校的学生信息表，它记录了全校学生的各种信息，每个学生的信息就是一个数据元素，这些元素共同构成了学生信息查找表。在这张表中，每一行代表一个学生的信息，包含学号、姓名、年龄、班级等字段，而每一列则代表学生的某一项属性，通过这样的组织方式，使得查找表中的数据既整齐又易于管理。

查找表在数据结构查找中起着基础性的作用，它是查找操作得以进行的前提。如果没有查找表来存储和组织数据，数据就会变得杂乱无章，查找目标数据将变得如同大海捞针一般困难。查找表的合理构建能够极大地提高查找的效率，比如通过对数据进行排序或者建立索引等方式，可以让计算机在查找时更快地定位到目标数据。

（二）关键字：数据的身份标识

关键字是数据元素中用于标识该元素的某个数据项的值，它就像是数据的 “身份证”，通过关键字，我们能够快速准确地识别和定位到特定的数据元素。关键字又可细分为主关键字和次关键字。主关键字能够唯一地标识一个数据元素，而次关键字则可以识别若干个数据元素 。

继续以学生信息表为例，“学号” 就是一个典型的主关键字。在一所学校里，每个学生都被分配了一个独一无二的学号，通过这个学号，我们可以精准地找到对应的学生信息，不会出现混淆。而 “姓名” 则可看作是次关键字，因为可能会有重名的学生存在，仅通过姓名查找，可能会得到多个学生的信息。

关键字在查找过程中扮演着至关重要的标识角色。当我们在查找表中进行查找操作时，实际上就是依据给定的关键字值，去查找表中与之匹配的数据元素。例如，当我们想要查询某个学生的成绩时，就可以通过输入该学生的学号这个关键字，在学生信息表中快速找到对应的记录，从而获取到他的成绩信息。准确地选择和使用关键字，是实现高效查找的关键之一。如果关键字选择不当，可能会导致查找结果不准确或者查找效率低下。

（三）查找操作：目标数据的定位

查找，简单来说，就是根据给定的某个值，在查找表中确定一个其关键字等于给定值的数据元素的过程 。比如在前面提到的学生信息表中，若我们想要查找学号为 “2023001” 的学生的详细信息，这就是一个查找操作。我们会在学生信息表中，逐个比对每个学生记录的学号字段，看是否与 “2023001” 相等，以此来定位到目标学生的信息。

查找的结果通常分为两种情况：查找成功和查找失败。当在查找表中找到了关键字与给定值相等的数据元素时，查找成功，此时可以返回该数据元素在查找表中的位置，或者返回该数据元素的具体信息。例如，若成功找到了学号为 “2023001” 的学生信息，就可以将该学生的姓名、年龄、班级等详细信息展示出来。而当查找表中不存在关键字与给定值相等的数据元素时，查找失败，此时一般会返回一些错误信息，比如失败标志、失败位置等，以便告知用户查找未成功的情况。

（四）静态与动态查找表：数据的静态与动态管理

根据查找表中数据元素是否可以动态变化，查找表可分为静态查找表和动态查找表 。静态查找表，顾名思义，是指在查找过程中，只对查找表进行查找操作，而不改动表中的数据元素，其内容在创建后相对固定 。比如学校用于存档的历史学生成绩表，一般情况下，这些成绩数据不会再被修改，我们只是偶尔会去查询某些学生在特定学期的成绩，这时候使用的就是静态查找表。它的优点是结构简单，实现容易，因为数据不会发生变化，所以查找算法的设计也相对简单。

动态查找表则允许在查找过程中同时进行插入数据元素或者删除数据元素的操作 。以电商平台的商品管理系统为例，商品的库存数量会随着销售和补货不断变化，新的商品也会不断上架，不再销售的商品会从系统中删除，这里使用的就是动态查找表。它的优势在于能够灵活地应对数据的动态变化，满足实际应用中对数据实时更新的需求，但由于数据的动态性，其实现和维护相对复杂，需要考虑插入和删除操作对查找效率的影响，以及如何保证数据结构的完整性和一致性等问题。

（五）平均查找长度：衡量查找效率的标尺

平均查找长度（Average Search Length，ASL）是衡量查找算法效率的一个重要指标，它表示在查找操作中，为了找到目标值所需进行的关键字比较次数的期望值 。简单来说，就是在各种可能的查找情况下，平均需要比较多少次关键字才能找到目标数据元素。

假设我们有一个包含 n 个数据元素的查找表，每个元素被查找的概率为 Pi，查找第 i 个元素所需的比较次数为 Ci，那么平均查找长度的计算公式为：ASL = ∑(Pi * Ci) （i 从 1 到 n） 。当每个元素被查找的概率相等时，公式可简化为：ASL = (1/n) * ∑Ci （i 从 1 到 n） 。例如，在一个有 5 个元素的查找表中，查找每个元素所需的比较次数分别为 1、2、3、4、5 次，且每个元素被查找的概率相等，那么根据公式计算可得，平均查找长度 ASL = (1/5) * (1 + 2 + 3 + 4 + 5) = 3 次 。

平均查找长度作为查找算法评价指标具有重要的意义。它能够直观地反映出一个查找算法的效率高低。一般来说，平均查找长度越小，说明查找算法的效率越高，因为在查找时需要进行的关键字比较次数越少，所需的时间也就越短。在实际应用中，我们通常会选择平均查找长度较小的查找算法，以提高数据处理的效率。不同的查找算法，其平均查找长度也会有所不同，比如顺序查找的平均查找长度较高，而二分查找在有序表中的平均查找长度则较低，通过对平均查找长度的分析和比较，我们可以根据具体的应用场景选择最合适的查找算法。

二、常见查找方法深度剖析

在了解了查找的基本概念后，接下来我们深入探讨几种常见的查找方法，它们各自有着独特的思想和应用场景，就像是不同类型的 “寻宝工具”，适用于不同的 “宝藏地图” 。

（一）顺序查找：简单直接的遍历查找

顺序查找，也叫线性查找，是一种最基本的查找技术，就像我们在书架上一本一本地寻找书籍一样，它的基本思想非常简单直接。在一个线性表中，从表的一端开始，顺序扫描线性表，依次将扫描到的结点关键字和给定值 K 相比较 。如果当前扫描到的结点关键字与 K 相等，那就表示查找成功；如果扫描结束后，都没有找到关键字等于 K 的结点，那就查找失败 。例如，在一个包含若干整数的数组[3, 7, 1, 9, 5]中查找数字9，顺序查找会从数组的第一个元素3开始，依次与9进行比较，直到找到数字9，确定查找成功。

下面是使用 Python 实现顺序查找的代码示例：

def sequential_search(arr, target):

for i in range(len(arr)):

if arr[i] == target:

return i

return -1

# 示例数组

array = [10, 15, 20, 25, 30]

# 查找目标值

target_value = 25

result = sequential_search(array, target_value)

if result != -1:

print(f"目标值 {target_value} 在数组中的索引为 {result}")

else:

print(f"目标值 {target_value} 不在数组中")

在时间复杂度方面，顺序查找在最坏情况下，需要比较 n 次才能确定目标元素是否存在（n 为线性表的长度），所以其时间复杂度为 O (n) 。

顺序查找的优点是算法简单，对表的结构没有任何要求，无论是用数组还是链表来存放结点，也不管结点之间是否按关键字有序，它都同样适用 。不过，它的缺点也很明显，就是查找效率低，当 n 较大时，查找所花费的时间会很长，因此不太适合大规模数据的查找 。比如在一个包含数百万个元素的数组中使用顺序查找，那查找过程可能会非常耗时。顺序查找比较适用于小规模数据或者数据无序且查找操作不频繁的场景。

（二）折半查找：有序数据的高效查找

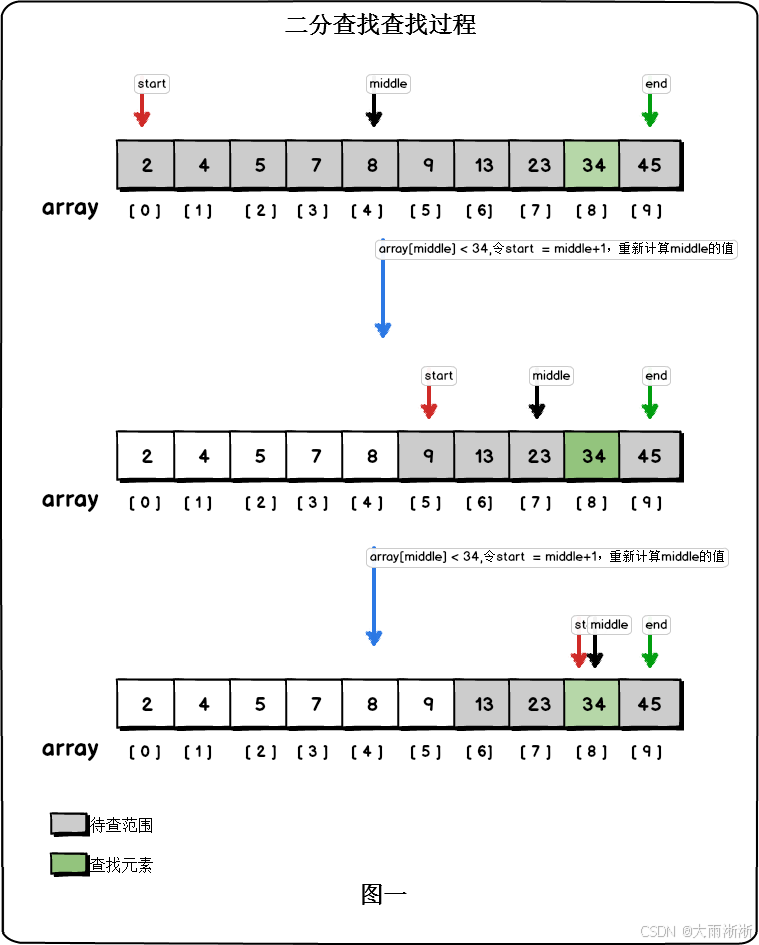
折半查找，也叫二分查找，是一种高效的查找方法，但它有一个前提条件，就是数据必须是有序的（升序或降序），并且数据存储结构支持随机访问，通常适用于顺序存储结构，如数组 。这就好比在一本按字母顺序编排的英语词典中查找某个单词，我们可以先翻到词典的中间部分，根据中间单词的首字母与目标单词首字母的比较，来确定目标单词在词典的前半部分还是后半部分，然后再在确定的那部分继续重复这个过程，直到找到目标单词。

折半查找的具体查找过程是这样的：假设有一个升序排列的数组，首先将查找值与数组中间位置的值进行比较 。如果相等，那就查找成功；如果不相等，且中间数据大于查找值，那么就继续在数组的前半部分查找；如果中间数据小于查找值，就继续在数组的后半部分查找 。每比较一次，就将查找范围缩小一半，直到找到目标值或者确定目标值不存在 。比如在数组[2, 4, 6, 8, 10, 12, 14]中查找数字8，首先计算中间位置，(0 + 6) // 2 = 3，中间元素是8，刚好与目标值相等，查找成功。

以下是折半查找的 Python 代码实现：

def binary_search(arr, target):

left, right = 0, len(arr) - 1

while left <= right:

mid = left + (right - left) // 2

if arr[mid] == target:

return mid

elif arr[mid] < target:

left = mid + 1

else:

right = mid - 1

return -1

# 示例数组

sorted_array = [3, 6, 9, 12, 15, 18, 21]

# 查找目标值

target_value = 12

result = binary_search(sorted_array, target_value)

if result != -1:

print(f"目标值 {target_value} 在数组中的索引为 {result}")

else:

print(f"目标值 {target_value} 不在数组中")

折半查找的时间复杂度为 O (log n) ，因为每次比较后都能将查找范围缩小一半，大大提高了查找效率 。不过，它的局限性在于要求数据必须有序，并且只能在顺序存储结构上使用 。如果数据是无序的，就需要先进行排序，而排序本身也需要消耗时间和资源；如果数据是存储在链表中，由于链表不支持随机访问，无法快速定位到中间元素，也就无法使用折半查找 。折半查找适用于数据量较大且数据已经有序的场景，比如在一个按学号升序排列的学生成绩表中查找某个学生的成绩，使用折半查找就能快速定位到目标学生的记录 。

（三）分块查找：结合顺序与折半的查找策略

分块查找，又称索引顺序查找，它结合了顺序查找和折半查找的优点，适用于数据量较大且数据分块有序的场景 。分块查找的条件是将查找表分为若干个子块，块内元素可以无序，但块之间是有序的，即第一个块中的最大关键字小于第二个块中的所有记录的关键字，第二个块中的最大关键字小于第三个块中的所有记录的关键字，以此类推 。同时，还需要建立一个索引表，索引表中的每个元素含有各块的最大关键字和各块中第一个元素的地址，并且索引表按关键字有序排列 。

分块查找的过程分为两步：第一步在索引表中确定待查记录所在的块，可以使用顺序查找或者折半查找索引表；第二步在确定的块内进行顺序查找 。例如，有一个关键字集合{88, 24, 72, 61, 21, 6, 32, 11, 8, 31, 22, 83, 78, 54}，按照关键码值为 24、54、78、88 分为四个块，并建立相应的索引表。当要查找关键字为 61 时，首先在索引表中通过顺序查找或折半查找确定 61 在第二个块中，然后在第二个块内进行顺序查找，最终找到 61 。

分块查找的平均查找长度为索引查找和块内查找的平均长度之和 。设索引查找和块内查找的平均查找长度分别为 L1 和 Ls，则分块查找的平均查找长度为 ASL = L1 + Ls 。当在块内和索引表中均采用顺序查找时，平均查找长度为 \((b + 1) / 2 + (s + 1) / 2\) （其中 b 为块数，s 为每块中的记录数）；若对索引表采用折半查找，则平均查找长度为 \(\lceil log_2(b + 1) \rceil + (s + 1) / 2\) 。

以大型图书管理系统为例，图书馆的藏书数量众多，为了便于查找，可以将图书按照类别（如文学、历史、科学等）进行分块，每个类别就是一个块，块内的图书按照入库时间等方式存放，不一定有序 。同时，建立一个索引表，记录每个类别的最大编号（或其他唯一标识）和该类别图书在书架上的起始位置 。当读者要查找某本图书时，首先通过索引表快速确定该图书所在的类别（块），然后在该类别对应的书架区域内进行查找，这样就能提高查找效率 。

（四）二叉排序树查找：树形结构的查找优势

二叉排序树，又称为二叉搜索树，它或者是一棵空树，或者是具有下列性质的二叉树：若它的左子树不空，则左子树上所有结点的值均小于它的根结点的值；若它的右子树不空，则右子树上所有结点的值均大于它的根结点的值；它的左、右子树也分别为二叉排序树 。例如，下面就是一棵二叉排序树：

5

/ \

3 7

/ \ / \

2 4 6 8

二叉排序树查找的过程如下：若二叉排序树为空树，则搜索失败；否则，若要查找的值 x 等于根结点的数据域之值，则查找成功；若 x 小于根结点的数据域之值，则搜索左子树；若 x 大于根结点的数据域之值，则搜索右子树 。比如在上面的二叉排序树中查找值为 6 的结点，首先与根结点 5 比较，6 大于 5，所以搜索右子树；在右子树中与 7 比较，6 小于 7，所以搜索 7 的左子树，最终找到值为 6 的结点，查找成功 。

在平均情况下，二叉排序树查找的平均查找长度与折半查找相近，为 O (log n) 。但在最坏情况下，即二叉排序树退化为单链表时，平均查找长度会变为 O (n) ，比如所有结点都只有右子树的情况。

二叉排序树在动态数据查找中有着广泛的应用 。比如在一个学生信息管理系统中，学生信息可以以二叉排序树的形式存储，每个结点包含学生的学号、姓名、成绩等信息 。当需要插入新的学生信息时，只需按照二叉排序树的插入规则，将新结点插入到合适的位置；当需要删除某个学生信息时，也可以按照相应的删除规则进行操作 。这样，在进行查找、插入和删除操作时，都能保持较高的效率 。

（五）散列表查找：基于哈希的快速查找

散列表，也叫哈希表，是一种根据关键码值而直接进行访问的数据结构 。它的基本概念是通过一个散列函数，把关键码映射到表中的一个位置来访问记录，以加快查找的速度 。这个映射函数就叫做散列函数，存放记录的数组就是散列表 。例如，我们可以设计一个散列函数hash(key) = key % 10，对于关键字集合{12, 25, 37, 43}，通过这个散列函数计算得到的散列地址分别为2、5、7、3 。

散列函数的构造方法有很多种，常见的有除留取余法、直接定址法、数字分析法、平方取中法、折叠法、随机数法等 。其中，除留取余法是最常用的一种方法，它的公式为hash(key) = key % p（p 为不大于散列表表长 m 的数，通常 p 取一个质数） 。比如，散列表表长为 13，对于关键字 26，通过除留取余法计算散列地址为26 % 13 = 0 。

由于关键码集合通常比散列表地址集合大得多，所以在使用散列函数时，可能会出现不同的关键码映射到同一个散列地址的情况，这就产生了冲突 。为了解决冲突，常用的方法有开放定址法和链地址法 。开放定址法是指当发生冲突时，通过某种探测方法在散列表中寻找下一个空的地址来存放冲突的元素 ，比如线性探测再散列，它的探测序列为Hi = (H(key) + i) % m（i = 1, 2, 3, …, m - 1 ，H (key) 为散列函数，m 为散列表长） 。链地址法是将所有散列地址相同的元素链接成一个链表，散列表中的每个位置存放的是链表的头指针 。例如，对于散列地址为 3 的位置，如果有多个关键字都映射到这个地址，就将这些关键字对应的元素依次插入到这个位置的链表中 。

散列表查找的性能非常高，在理想情况下，即没有冲突发生时，查找的时间复杂度为 O (1) ，可以直接通过散列函数计算得到的地址找到目标元素 。但在实际应用中，冲突是难以避免的，当冲突较多时，查找性能会受到一定影响 。不过，通过合理地选择散列函数和处理冲突的方法，可以将冲突控制在一个较低的水平，从而保证散列表查找的高效性 。

以内存缓存系统为例，在计算机系统中，内存缓存用于存储经常访问的数据，以提高数据的访问速度 。可以将数据的标识（如数据的 ID）作为关键字，通过散列函数计算出散列地址，将数据存储在散列表中对应的位置 。当需要访问数据时，只需根据数据的 ID 通过散列函数计算散列地址，就可以快速地从散列表中找到对应的缓存数据，大大提高了数据的访问效率 。

三、实战演练：数据结构查找的应用

了解了常见的查找方法后，接下来我们通过几个实际案例，来看看数据结构查找在不同系统中的具体应用，以及如何根据实际需求选择合适的查找方法。

（一）学生成绩管理系统中的查找应用

在学生成绩管理系统中，查找学生成绩是一项非常频繁的操作。我们可以利用顺序查找和折半查找等方法来实现这一功能。

假设我们有一个学生成绩列表，每个学生的成绩记录包含学号、姓名和成绩等信息。如果使用顺序查找，当需要查找某个学生的成绩时，我们会从列表的第一个元素开始，逐个比较每个学生的学号或姓名，直到找到目标学生的成绩记录。例如，下面是一个简单的 Python 实现：

students = [

{'id': 1, 'name': 'Alice','score': 85},

{'id': 2, 'name': 'Bob','score': 90},

{'id': 3, 'name': 'Charlie','score': 78}

]

def sequential_search_student(students, target_id):

for student in students:

if student['id'] == target_id:

return student

return None

target_student_id = 2

result = sequential_search_student(students, target_student_id)

if result:

print(f"找到学生 {result['name']}，成绩为 {result['score']}")

else:

print("未找到目标学生")

如果学生成绩列表是按照学号或姓名有序排列的，我们就可以使用折半查找来提高查找效率。折半查找的实现如下：

students.sort(key=lambda x: x['id'])

def binary_search_student(students, target_id):

left, right = 0, len(students) - 1

while left <= right:

mid = left + (right - left) // 2

if students[mid]['id'] == target_id:

return students[mid]

elif students[mid]['id'] < target_id:

left = mid + 1

else:

right = mid - 1

return None

target_student_id = 2

result = binary_search_student(students, target_student_id)

if result:

print(f"找到学生 {result['name']}，成绩为 {result['score']}")

else:

print("未找到目标学生")

顺序查找的优点是实现简单，对数据的顺序没有要求，适用于小规模数据或者数据无序的情况。但它的缺点也很明显，查找效率低，当数据量较大时，查找时间会很长。折半查找则适用于数据量较大且数据有序的情况，它的查找效率高，时间复杂度为 O (log n) ，但前提是数据必须有序，并且只能在顺序存储结构上使用。

（二）图书管理系统中的书籍检索

在图书管理系统中，需要快速准确地找到读者所需的书籍。分块查找和二叉排序树查找是常用的实现书籍检索功能的方法。

假设我们将图书按照类别分为多个块，每个块内的图书按照书名的字典序排列，并建立了一个索引表，记录每个块的最大书名和块内第一本书的位置。当读者输入书名进行查找时，首先在索引表中使用折半查找确定目标书籍所在的块，然后在该块内使用顺序查找找到目标书籍。以下是一个简单的 Python 示例：

# 假设已经按照类别分块，并建立了索引表

index_table = [

{'max_title': 'C++ Primer', 'block_start': 0},

{'max_title': 'Python Crash Course', 'block_start': 5},

{'max_title': 'The Mythical Man - Month', 'block_start': 10}

]

books = [

'C++ Primer', 'Effective C++', 'C++ Templates', 'STL源码剖析', '深度探索C++对象模型',

'Python Crash Course', 'Learning Python', 'Python Cookbook', 'Fluent Python', 'Python核心编程',

'The Mythical Man - Month', '人月神话', '代码大全', '设计模式', 'Clean Code'

]

def block_search(books, index_table, target_title):

left, right = 0, len(index_table) - 1

while left <= right:

mid = left + (right - left) // 2

if target_title <= index_table[mid]['max_title']:

block_start = index_table[mid]['block_start']

for i in range(block_start, len(books)):

if books[i] == target_title:

return i

elif books[i] > target_title:

break

return -1

else:

left = mid + 1

return -1

target_book = 'Python Cookbook'

result = block_search(books, index_table, target_book)

if result != -1:

print(f"找到书籍，索引为 {result}")

else:

print("未找到目标书籍")

如果使用二叉排序树来存储图书信息，每个节点包含书名、作者、ISBN 等信息，并且左子节点的书名小于当前节点的书名，右子节点的书名大于当前节点的书名。这样，在查找书籍时，就可以利用二叉排序树的特性，快速定位到目标书籍。以下是一个简单的 Python 类实现：

class BookNode:

def __init__(self, title, author, isbn):

self.title = title

self.author = author

self.isbn = isbn

self.left = None

self.right = None

class BookTree:

def __init__(self):

self.root = None

def insert(self, title, author, isbn):

new_node = BookNode(title, author, isbn)

if not self.root:

self.root = new_node

else:

current = self.root

while True:

if title < current.title:

if not current.left:

current.left = new_node

break

else:

current = current.left

else:

if not current.right:

current.right = new_node

break

else:

current = current.right

def search(self, target_title):

current = self.root

while current:

if target_title == current.title:

return current

elif target_title < current.title:

current = current.left

else:

current = current.right

return None

book_tree = BookTree()

book_tree.insert('C++ Primer', 'Stanley Lippman', '9780321714114')

book_tree.insert('Python Crash Course', 'Eric Matthes', '9781593276034')

book_tree.insert('The Mythical Man - Month', 'Frederick P. Brooks Jr.', '9780201835953')

target_book = 'Python Crash Course'

result = book_tree.search(target_book)

if result:

print(f"找到书籍，作者为 {result.author}，ISBN为 {result.isbn}")

else:

print("未找到目标书籍")

分块查找结合了顺序查找和折半查找的优点，适用于数据量较大且数据分块有序的场景。二叉排序树查找则利用了树形结构的优势，在动态数据查找中表现出色，插入和删除操作也相对高效，但在最坏情况下，二叉排序树可能退化为单链表，导致查找效率降低。

（三）数据库索引中的查找技术

在数据库中，索引是提高数据查询效率的关键技术之一。B 树和 B + 树是数据库索引中常用的数据结构。

B 树是一种多路平衡查找树，它的每个节点可以包含多个关键字和子节点。在 B 树中，所有的关键字都分布在整棵树中，并且任何一个关键字出现且只出现在一个节点中。查找时，从根节点开始，对节点内的关键字序列进行二分查找，如果命中则结束，否则进入查询关键字所属范围的子节点，重复这个过程，直到找到目标关键字或确定其不存在。例如，下面是一个简单的 3 阶 B 树示意图：

5

/ | \

2 4 7

/ \ / \ / \

1 3 6 8 9 10

B + 树是 B 树的变体，它与 B 树的主要区别在于：所有的数据记录都存储在叶子节点，非叶子节点仅存储关键字和指向子节点的指针；叶子节点包含了所有的关键字，并且通过指针串联成有序链表。在 B + 树中，查找操作必须遍历到叶子节点才能找到数据，这使得 B + 树的查询路径长度总是等于树高，性能更加稳定。例如，下面是一个简单的 3 阶 B + 树示意图：

5

/ | \

2 4 7

/ \ / \ / \

1 3 6 8 9 10

| | | | | |

11 12 13 14 15 16

以 MySQL 数据库为例，InnoDB 存储引擎的索引结构采用的就是 B + 树。当执行查询语句时，数据库会根据索引的 B + 树结构快速定位到目标数据所在的叶子节点，从而提高查询效率。例如，对于查询语句SELECT * FROM students WHERE id = 10 ，如果在id字段上建立了 B + 树索引，数据库会从 B + 树的根节点开始，通过比较关键字快速找到包含id = 10的叶子节点，然后返回对应的记录。

B 树和 B + 树在数据库索引中的应用，充分利用了它们的特性，减少了磁盘 I/O 次数，提高了数据查询的效率。B + 树由于其叶子节点的有序链表结构，在范围查询（如SELECT * FROM students WHERE id BETWEEN 5 AND 10 ）和分页查询等操作中表现出更高的效率 。

四、总结与展望：数据结构查找的未来之路

数据结构查找作为计算机科学领域的基础技术，在各种信息系统中扮演着举足轻重的角色 。它的基本概念，如查找表、关键字、查找操作、静态与动态查找表以及平均查找长度等，构成了我们理解和应用查找技术的基石 。通过对顺序查找、折半查找、分块查找、二叉排序树查找和散列表查找等常见查找方法的深入剖析，我们看到了不同查找方法的独特优势和适用场景 。

在实际应用中，数据结构查找广泛应用于学生成绩管理系统、图书管理系统、数据库索引等众多领域，为提高系统的运行效率和用户体验发挥了关键作用 。根据不同的应用需求选择合适的查找方法，能够显著提升数据处理的速度和准确性 。

随着大数据和人工智能等新兴技术的快速发展，数据结构查找也面临着新的机遇和挑战 。在大数据时代，数据量呈指数级增长，对查找算法的效率和可扩展性提出了更高的要求 。未来，查找技术有望在以下几个方面取得突破和发展 。

在大数据处理方面，研究更加高效的分布式查找算法将成为重点，以应对海量数据的存储和查询需求 。例如，基于分布式哈希表（DHT）的查找算法，可以将数据分布在多个节点上，实现快速的并行查找 。同时，结合云计算技术，利用云平台的强大计算和存储能力，实现大数据的高效查找和分析 。

在人工智能领域，查找技术将与机器学习、深度学习等技术深度融合 。例如，在图像识别和自然语言处理中，通过构建高效的索引结构和查找算法，可以快速检索和匹配相关的数据，提高模型的训练和推理效率 。此外，利用人工智能技术自动优化查找算法的参数和策略，实现查找性能的自适应提升 。

未来，数据结构查找技术还可能在量子计算、区块链等新兴领域发挥重要作用 。随着量子计算技术的发展，量子查找算法有望实现比传统算法更快的查找速度，为解决复杂的科学和工程问题提供新的思路 。在区块链中，查找技术可以用于快速验证交易的合法性和查询区块链的状态 。

数据结构查找作为计算机科学的核心技术之一，将在不断发展的信息技术浪潮中持续演进和创新 。我们有理由期待，在未来，数据结构查找技术将为我们打开更多通往高效信息处理和智能应用的大门，为推动社会的数字化和智能化发展做出更大的贡献 。