FOC中SVPWM关于调制问题的理解

SVPWM相比SPWM具有更高的直流电压利用率。SPWM的线电压峰值仅为0.866Udc，而SVPWM通过优化调制方式可达到Udc。其核心在于：1）利用空间矢量合成，最大输出电压为Udc/√3；2）采用马鞍波调制，注入三次谐波"削平"波形，在不发生过调制的情况下提升15.47%的利用率；3）当调制比M=1时对应线性调制范围。这种技术使逆变器输出线电压达到直流母线电压水平，显著提高了电能转换效率。

weixin_63295750

590人浏览 · 2025-08-30 21:42:14

weixin_63295750 · 2025-08-30 21:42:14 发布

我们首先阐述为什么要使用SVPWM：因为SPWM的直流电压利用率小造成浪费

分析：

相电压Vphase：电机每相对中心点之间的电压 (逆变器的Vphase = Udc / 2)

线电压Vline：任意两相之间的电压差,而Vline = Vphase * sqrt(3)

直流电压利用率：线电压与直流电压之比

SPWM线电压Vline = Vphase * sqrt(3) = Udc / 2 * sqrt(3) = 0.866Udc，利用率0.866造成浪费

为什么用SVPWM？

SVPWM的直流母线电压利用率为：Vline = Vphase * sqrt(3) = Udc/sqrt(3)* sqrt(3) = Udc

此时直流母线电压利用率为1

可以看到，SPWM的直流电压利用率是 0.866会造成浪费，故我们采用更高效的SVPWM，即期望线电压为Udc

1.数值关系

在SVPWM中，由开关管状态生成的六个基本非零电压的幅值为,由Clark变换:

$T_{3s/2s}=\frac{2}{3} \begin{bmatrix} 1 & -\frac{1}{2} & -\frac{1}{2} \\ \\ 0 & \frac{\sqrt3}{2} & -\frac{\sqrt3}{2} \end{bmatrix}$

在开关管（100）状态，Ua=Udc,Ub=0,Uc=0,Ualpha和Ubeta的值为：即 $\left[\begin{array}{l} U_{\alpha} \\ U_{\beta} \end{array}\right] = \frac{2}{3} \left[\begin{array}{ccc} 1 & -\frac{1}{2} & -\frac{1}{2} \\ 0 & \frac{\sqrt{3}}{2} & -\frac{\sqrt{3}}{2} \end{array}\right] \left[\begin{array}{l} U_{a} \\ U_{b} \\ U_{c} \end{array}\right]$

即Ualpha = 2/3Udc

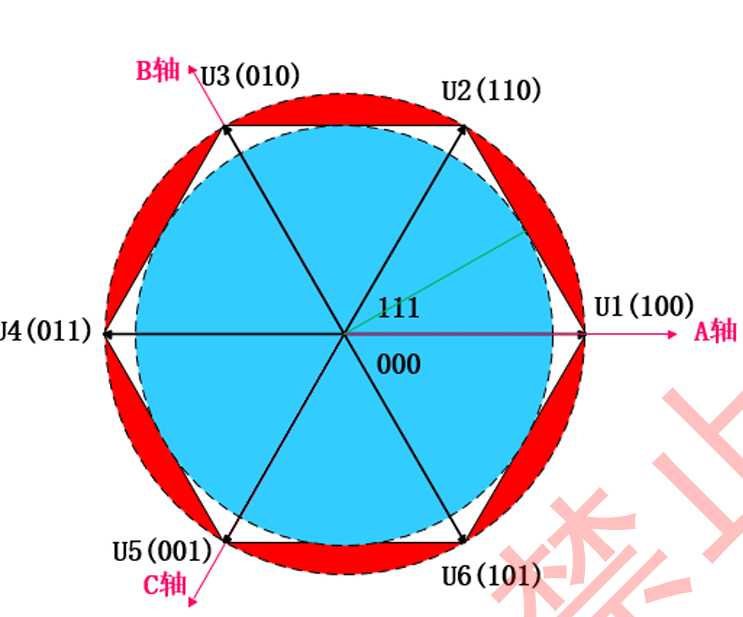
在上图中，开关状态 (1,0,0) 对应的空间电压矢量 U1 位于α轴上，其幅值为 2/3Udc

即：六边形外切圆的半径为 2/3Udc

根据三角形关系，得到内切圆半径(上图绿色的线)即我们所能达到的所需电压的最大幅值为Uout = Uref = Udc/sqrt(3)

2.关于调制比：

定义：调制波幅峰值和载波峰值的比值，其中Aref是调制波的峰值，Af是载波的峰值

$m = \frac{A_{\mathrm{ref}}}{A_{f}}$

而在SVPWM中，我们定义调制比为： $M = \frac{\sqrt{3} U_{\mathrm{m}}}{U_{\mathrm{dc}}}$ ，式子中，Um即为Uout

问题：我们为什么要这么定义调制比？

回答：SVPWM中，我们定义载波电压为逆变器能输出的最大峰值电压即六边形内切圆，即为内切圆半径，为Udc/sqrt(3),定义调制波为我们生成给定电压的模长Uout,

（1）若我们生成所需的电压为内切圆的Uref = Udc/sqrt(3)，带入上式调制比公式得到M=1，即在线性调制范围内，此时多为同步调制（即载波频率不变）

（2）若我们生成所需的电压为外切圆的Uref = 2/3Udc，带入上式调制比公式得到M=1.154，即在非线性调制范围内，此时合成的电压矢量不是完美的圆

3.马鞍波的作用（提高母线电压利用率）

在前面我们已经提到，在不发生过调制的情况下，SVPWM能输出的相电压峰值为Udc/sqrt(3),即线电压最大峰值为Udc，即我们希望得到线电压为幅值最大为Udc的完美正弦波。而若我们以标准的幅值最大为Udc的正弦波为调制波，(即SPWM）,理论上调制波和载波比最大为1，输出相电压峰值为Udc/2小于Udc/sqrt(3),电压利用率小

Udc/sqrt(3) / Udc/2 = 1.1547，即SVPWM比SPWM利用率提高15.47%

而若再增大正弦调制波幅值会造成过调制。

如何在不造成过调制的情况下提高母线电压的利用率？

我们在标准正弦波的基础上注入三次谐波，让正弦波的顶被“削平”，即降低了调制波的幅值，而三相的三次谐波会相互抵消，不会出现在最终的线电压输出里，而马鞍波作为调制波在调制后生成的基波分量是相电压峰值为Udc/sqrt(3)即最大线电压Udc