容错控制概述（含推导）1. 系统描述2. 估计器设计4. 稳定性证明（重难点！！）5. 线性矩阵不等式（LMI）与舒尔补定理（Schur Complement）1. 系统描述设我们有如下线性系统{x˙=Ax+Bu+Efy=Cx(1)\begin{cases}\begin{aligned}\dot{x} &= Ax + Bu + Ef \\y &= Cx\end{aligned}\e

优化方法理论合集第8弹——庞特里亚金最大值原理。介绍了庞特里亚金最大值原理的内容，并列出了求解方法。

因此，由(3–1)得到的通解(3–2–1)所表示的动态过程也被称为“，即式(3)等号右边为0、式(3–1)的情况。对比式(3)和式(3–1)，不难发现，(3–1)是(3)将等号右边项置零得到的，即。上述分析表明：一个函数直接进行拉氏变换得到的复平面表达式，和其先进行泰勒展开后进行拉氏变换得到的复平面表达式，是相同的。将泰勒展开应用在函数线性化中时，只取线性化的第一项，后面的高阶项全部用高阶小量表示

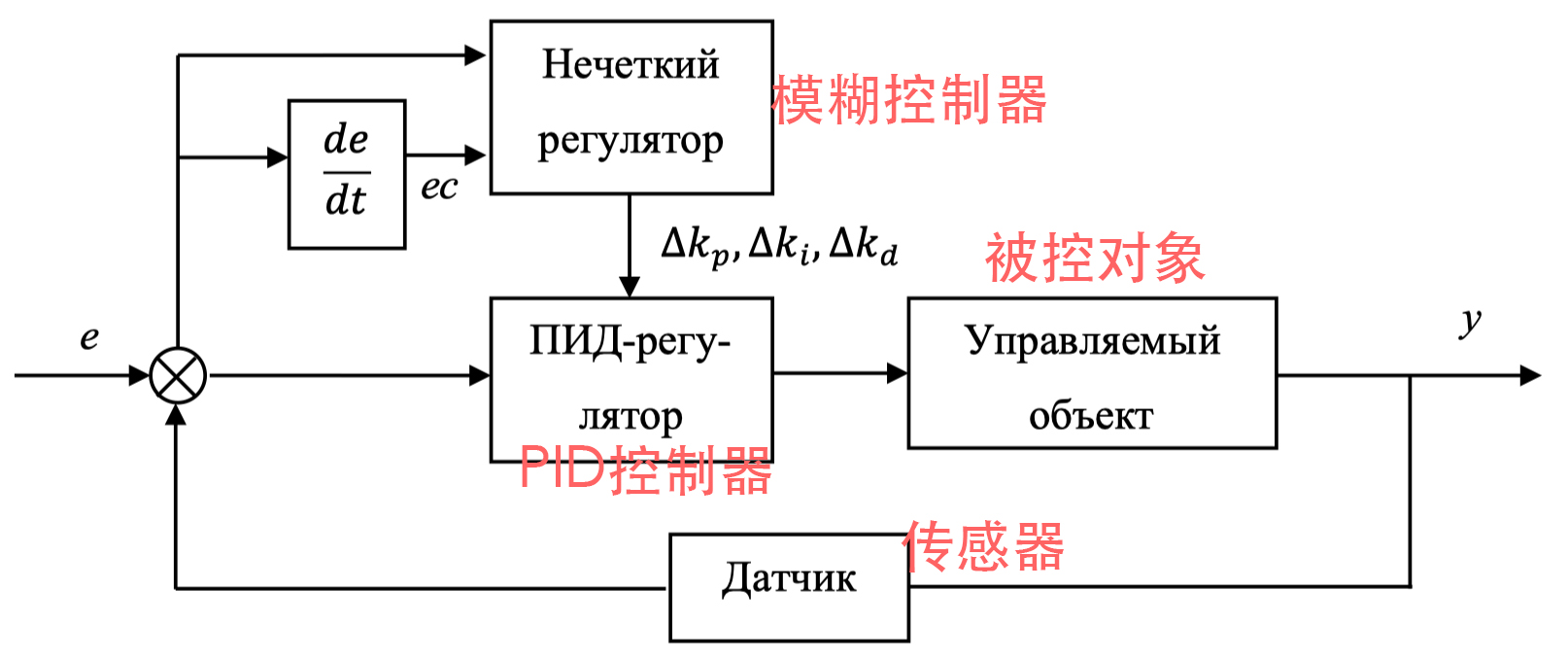
模糊控制笔记（三）模糊控制系统与模糊PID1. 模糊控制系统1) 量化2) 模糊控制系统组成3) 模糊规则2. 模糊PID本文章所有知识点均为作者本人学习刘杰、李允公等老师的教材《智能控制与MATLAB实用技术》时所作笔记，在此发自肺腑地表达对老师们辛勤劳动的感谢和尊敬，也安利一下这本书，对入门智能控制的同学们来说是一本极其优秀的教材！1. 模糊控制系统1) 量化一般地，根据输入信号的取值，将其分

动态表面控制DSC简单介绍1. 动态表面控制由来2. 动态表面控制的理论介绍1) 李雅普诺夫函数V1V_1V1​的设计与求导2) 李雅普诺夫函数V2V_2V2​的设计与求导3) 总体李雅普诺夫函数V3V_3V3​的设计与求导1. 动态表面控制由来动态表面控制（Dynamic Surface Control, DSC）是非线性控制领域的一种方法，基于李雅普诺夫稳定性理论，其构建方式和过程与反步法（B

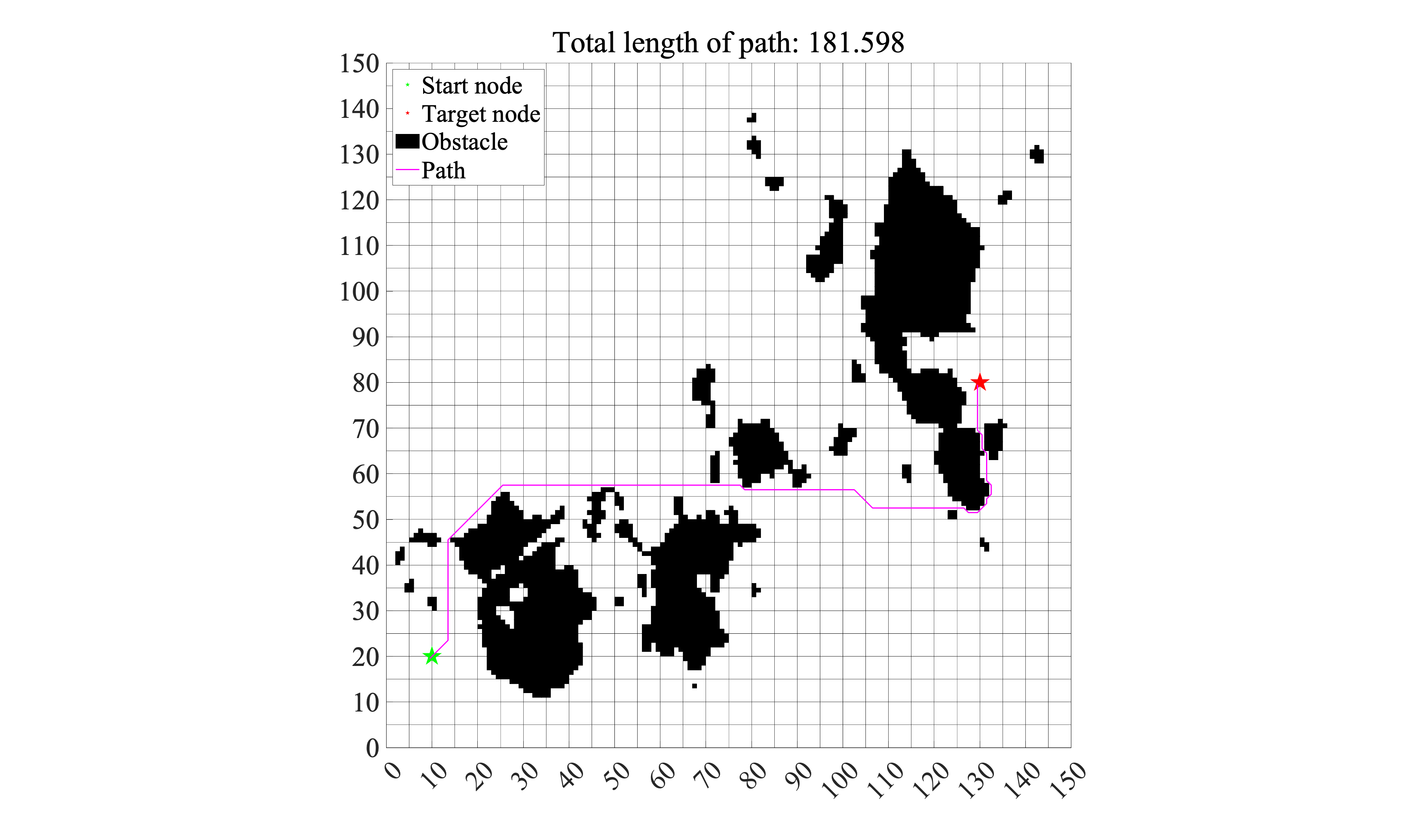
A*搜索算法简介及保姆级代码解读1. A*算法简单介绍1.1 A*算法理论基础1.1.1 节点计算1.1.2 由计算得出的小结论1.2 算法逻辑结构2. 代码解析2.1 引入地图2.2 预处理2.3 定义父节点`parent`2.4 主循环1. A*算法简单介绍A*算法是一种路径规划算法，和传统的Dijkstra算法有所不同，该算法有选择地进行节点搜索，因此比Dijkstra算法更快、搜索的点更少

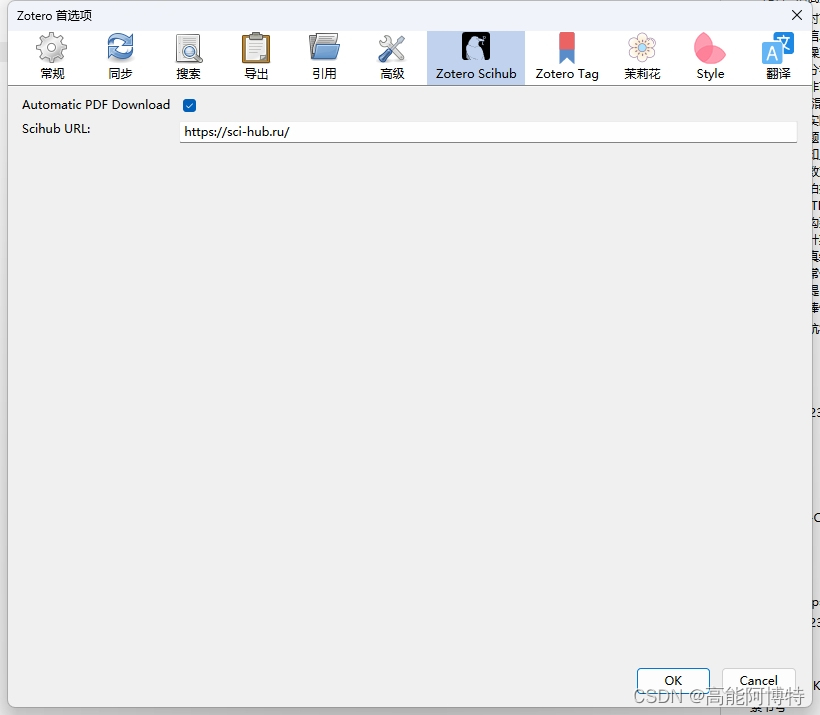
如果还未解决，可以点击Zotero中的编辑——首选项——茉莉花——中文插件设置，最下方有一个“PDFtk Server路径设置”，检查此处是否是绿色对钩。链接里先下载一个PDFtk Server，安装好，记好安装路径，之后在编辑——首选项——茉莉花——中文插件设置——PDFtk Server路径设置 中，设置为该安装路径，最后重启Zotero。在每次打开Zotero后，第一件做的事就去“编辑”——

整理了目前网上关于mac推出移动硬盘失败的解决方法

温馨提示：在阅读本文之前，读者最好具有一定的的相关知识，可以阅读笔者的另一篇博客中的第1节来了解。