赫尔德不等式就像数学界的能量饮料，为我们提供了强大的工具，帮助我们在数学的海洋中遨游。无论你是初学者还是资深数学家，理解并应用这个不等式，都能让你的数学之旅更加顺畅。希望这篇博客能让你对赫尔德不等式有一个全新的认识。如果你觉得数学有点“苦涩”，不妨想象自己喝了一罐能量饮料，继续探索吧！

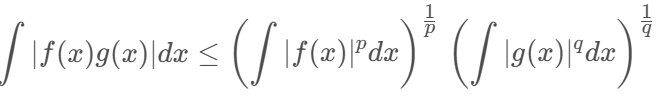
传染病模型成为了热门话题。但你知道这些模型是怎么建立的吗？它们背后的数学原理是什么？别担心，即使你数学只学到九九乘法表，今天也能听懂！

小型火箭初始质量为1400千克，其中包括1080千克燃料。火箭竖直向上发射时燃料以18千克/秒的速率燃烧掉，由此产生32000牛顿的恒定推力。当燃料用尽时引擎关闭。设火箭上升的整个过程中，空气阻力与速度的平方成正比，比例系数为0.4（千克/米）。重力加速度取9.8米/秒2.

你是否曾好奇过，世界上所有的兔子是怎么保持生生不息的？别着急，今天就让我们一起来了解一个特别有趣的数学模型——莱斯利（Leslie）种群模型。这个模型不仅帮助我们理解兔子种群是如何以不同的年龄段进行增长的，还能带领我们走入更加广泛的生态学与生物学世界。坐稳了，接下来的一段旅程充满了数学、图表、编程以及很多幽默。

在古代，数学家和科学家为了求出圆周率 π 费尽了心思，尝试了无数方法。法国数学家乔治·蒲丰 (Georges-Louis Leclerc, Comte de Buffon) 则另辟蹊径，在1777年提出了一个听起来很奇怪的方法——**投针实验**。他的方法居然可以通过丢针来近似计算 π。今天，我们就来聊聊这个看似无厘头却妙趣横生的数学实验：蒲丰投针实验。

当数学遇上超级英雄在数学的宇宙中，微分方程就像是无尽的星辰，充满了神秘与挑战。面对这些复杂的方程，我们需要的不仅是智慧，更需要一种强大的武器——这就是龙格库塔法（Runge-Kutta Method）。它就像数学界的超级英雄，能够在复杂的方程面前轻松应对，带领我们穿越计算的迷雾，找到精确的数值解。