《强化学习推荐系统中的汤普森采样探索策略》介绍了推荐系统中强化学习的探索策略，重点阐述了汤普森采样方法。汤普森采样通过贝叶斯推断估计每个动作的最优概率，利用Beta分布作为先验分布，结合观测数据更新后验分布。该方法能有效平衡探索与利用，适用于二值奖励场景，通过参数调整动态优化策略。文章包含数学推导和Python实现代码，展示了该策略在5臂赌博机问题中的应用。

导入pandas库和numpy库import pandas as pdimport numpy as np我们以一个csv文件来展示pandas是如何来进行数据预处理的：titanic_train.csv读入文件titanic_train.csv，并显示前十行数据titanic_survival = pd.read_csv("titanic_train.csv")tit...

现今我们所谓的“古彝文”指的是在民间流通使用的原生态彝文，据《滇川黔桂彝文字集》显示，这种文字多达87046字；在国家图书馆珍藏中，由这些文字书写的古彝文典籍共有592册（件），可见其蕴含着巨大的文化价值和实用价值。在当代，彝文依然拥有广泛的受用人群。四川省曾在1980年发布规范彝文共819字，截止2012年，滇川黔桂发布的通用彝文有5598字。这两种彝文常用于仪式、节庆、旅游景点等场合——彰显彝

打开控制面板，选中Office，点击修复，在弹出的窗口中选择快速修复或者联机修复都可以，然后等待修复完成即可。

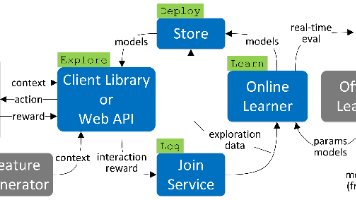
Decision Service框架将整条强化学习链路拆解为探索（Explore）、记录（Log）、学习（Learn）、部署（Deploy）四个可独立演进却首尾相接的模块。想要学到“成年人偏好政治新闻、青少年偏好体育新闻”这类映射，就不能再用传统监督学习的思路，而需要借助上下文多臂赌博机（contextual bandit）等强化学习方法，通过精心涉及的系统来解决探索、偏差和延迟带来的挑战。

文章目录1. Model-Free 与 Model-Based RL2. Policy-Based 与 Value-Based RL3. Monte-Carlo Update 与 Temporal-Difference Update RL4. On-Policy 与 Off-Policy RL1. Model-Free 与 Model-Based RL根据Agent是否理解其所处的环境，可以将强化

昆仑万维集团作为中国领先的互联网平台出海企业，逐渐在全球范围内形成了海外信息分发及元宇宙平台Opera、海外社交娱乐平台StarX、全球移动游戏平台Ark Games、休闲娱乐平台闲徕互娱、投资板块等五大业务，市场遍及中国、东南亚、非洲、中东、北美、南美、欧洲等地，为全球互联网用户提供社交、资讯、娱乐等信息化服务。在训练自编码器时，为了避免潜在表示空间出现高度的异化，作者使用了两种正则化方法，一种

在有些数据集中，有些数据变量用字符串表示，但为了方便处理，往往想转换为好处理的格式，这时候不一定要用one hot进行编码，也可以直接转成整数：test_df["xx"] = pd.factorize(test_df["xx"])[0].astype(int)效果gift_cards["user_id"] = pd.factorize(gift_cards["user_id"])[0].astyp

1、①xdx=12dx2xdx = \frac{1}{2}dx^2②xndx=1n+1dxn+1x^ndx = \frac{1}{n+1}dx^{n + 1}③1x√dx=2dx√\frac{1}{\sqrt{x}}dx = 2d\sqrt{x}④1x2dx=−d1x\frac{1}{x^2}dx = -d\frac{1}{x}2、①axdx=1lnadaxa^xdx = \fr

我们构造一个简单的神经网络，通常情况下n_output是分类数量，例如二分类任务那n_output=2、六分类任务那么n_output=6class Net(torch.nn.Module):def __init__(self, n_feature, n_hidden, n_output):super(Net, self).__init__()self.inLayer = torch.nn.Lin