进化算法是啥？——一堂给聪明懒人的“自然开挂”入门课

南方的狮子先生

---

开场白
“如果连蚂蚁都不会写代码，凭啥让我调参到秃？”
别急，今天咱们讲一种“把大自然当免费打工人”的黑科技——进化算法（Evolutionary Algorithms，简称 EA）。它不需要你懂高数，也不怕你把问题描述得乱七八糟，只要你能回答一句“哪个解更好？”，它就能帮你一路开挂。读完这篇，你可以放心把“调参锅”甩给达尔文。

---

一、先解决三个灵魂拷问

1. 我又不养电子宠物，为啥要学它？
   因为传统算法太“玻璃心”：数据一脏就崩溃，维度一高就罢工。进化算法天生“社牛”，噪声、多峰、动态环境统统“佛系”处理。
2. 我数学只会九九乘法表，能玩吗？
   能！EA 唯一需要的数学是——比大小。
3. 会不会跑一晚上结果还不如我手动试三次？
   只要你比它更懂问题，当然手动更快；但当你有 20 个参数、每个参数 100 种取值时，手动试完大概需要宇宙寿命的 1/3。

---

二、把大象装进冰箱……哦不，把进化搬进电脑 🐘➡️💻

大自然版	电脑版
生得多 🥚🥚🥚	随机生成一群解 🎲
长得不一样 🧬	计算谁更牛 🏆
谁强谁脱单 💘	让牛人配对生娃 👫➡️👶
生得更多 ➕	娃偶尔突变 🧪
循环 N 代 🔄	替代老家伙 🧓➡️🧒

> 一句话总结：EA 就是“用种群代替单点、用相亲代替梯度、用突变代替灵感”的 暴力美学 💥

---

🚄 vs 🚙 梯度下降 VS 进化算法

场景	梯度下降 (GD)	进化算法 (EA)
轨道光滑	高铁飙车 🚄💨	皮卡也能跑 🚙
断壁残垣	翻车 😵	四轮驱动 💪
离散沙漠	没油了 ⛽❌	沙地模式 ✅
黑箱泥潭	看不见 👀❌	盲开也行 ✅
评估超贵	一票难求 💸	并行 100 辆 🚙🚙🚙

> 口诀：
> 低维光滑 → GD 冲锋 ⚔️
> 高维崎岖/离散/黑箱/贵评估 → EA 开道 🚧
> 先用 EA 翻山找坑 🏔️，再换 GD 精修 🔧，动态环境再切回 EA 🔄，左右互搏，才是真·满级选手 🏅

---

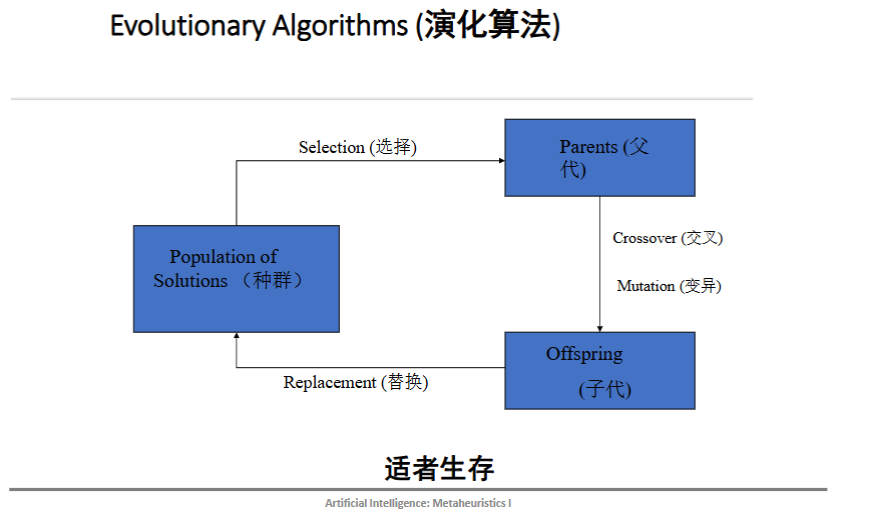
三、5 行伪代码，比 Python 还短

随机生一群解（种群）
while 还没满意:
    算每个人（解）的战斗力（适应度）
    战斗力高的去相亲（选择）
    配对生娃（交叉），娃再整点容（突变）
    让娃和老家伙竞争，留下更好的
    世代 += 1

看完这段，你已经掌握了 90% 的“核心科技”，剩下的只是“怎么相亲、怎么生娃”的细节。

---

严谨解释版本：

以下是对“Generate-and-Test”方法各步骤的严谨解释，面向希望深入理解其逻辑与内涵的初学者：

Generate-and-Test: Description of steps

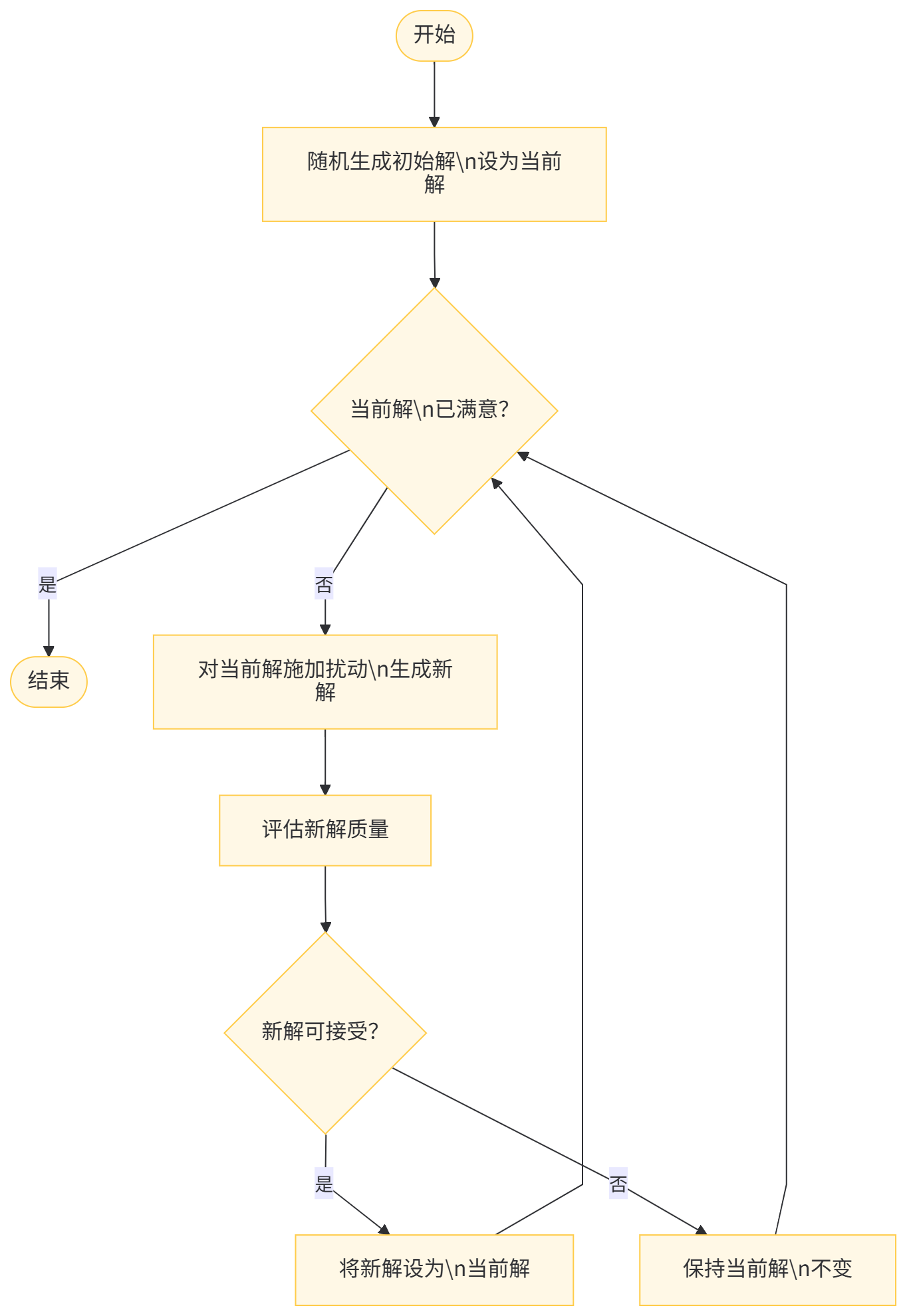
1. Generate the initial solution at random and denote it as the current solution.
（随机生成初始解，并将其设为当前解。）

• 该步骤为算法的起点。由于尚未获得任何关于问题的信息，通常采用随机方式在解空间中选取一个候选解。
• 此解将作为后续搜索的基础，称为“当前解”（current solution）。
• 随机初始化保证了算法在理论上具备探索整个解空间的可能性，避免人为偏见。

2. Generate the next solution from the current one by perturbation.
（通过对当前解施加扰动，生成下一个解。）

• 该步骤体现了算法的局部搜索机制。通过对当前解进行微小变动（即“扰动”，perturbation），产生一个“邻居解”或“候选解”。
• 扰动方式依赖于问题的表示形式，例如：
  • 在离散优化中，可能是交换两个元素、翻转某个二进制位；
  • 在连续优化中，可能是加入高斯噪声或沿某方向移动一小步。
• 此过程不需要梯度信息，因此适用于不可导、黑箱或离散问题。

3. Test whether the newly generated solution (next solution) is acceptable;
（测试新生成的解是否可接受。）

• “可接受”通常定义为：

  • 新解优于当前解（适用于爬山法等贪婪策略）；
  • 或新解满足某种概率条件（如模拟退火中的Metropolis准则）；
  • 或新解不违反约束条件（在约束优化中）。

  1. Accept it as the current solution if yes;
  （若可接受，则将其设为当前解。）

  2. Keep the current solution unchanged otherwise.
  （否则，保持当前解不变。）

4. Go to Step 2 if the current solution is unsatisfactory, stop otherwise.
（若当前解仍不满足终止条件，则返回步骤2；否则，停止算法。）

• 该步骤控制算法的迭代流程。
• “不满意”通常由以下终止条件判断：
  • 达到最大迭代次数；
  • 解的质量满足预设阈值；
  • 连续多代无改进（收敛）。
• 若未满足终止条件，则返回步骤2，继续“扰动 → 测试 → 接受/拒绝”的循环，体现算法的迭代改进机制。

---

总结：Generate-and-Test 的核心思想

Generate-and-Test 是一种基于迭代的局部搜索框架，其本质可概括为：

“在当前解的基础上，通过扰动生成新解，并根据质量评估决定是否接受，从而逐步逼近更优解。”

---

四、小试牛刀：31 以内找最大的 x²

问题简单到爆，但请假装你是火星人，完全不会解。

1. 编码：用 5 位二进制表示 0–31，比如 01101 = 13。
2. 初始种群：随机抽 4 串二进制，像抽签。
3. 算适应度：直接拿 x² 当分数，越大越香。
4. 相亲：转盘赌——分数越高，指针停你身上的概率越大。
5. 生娃：随机挑交叉点，比如
   爸爸 011|01
   妈妈 110|00
   切一刀，交换后半段，得 01100 和 11001。
6. 突变：随机挑 1 位翻转，0→1 或 1→0，防止“近亲结婚”。
7. 新一代上岗，老的卷铺盖。
   跑 10 代后，种群里几乎全是 11111（=31）。你啥也没干，却“进化”出了正确答案！

---

五、常见算法家谱（背口诀就行）

• 遗传算法 GA：老牌明星，爱用二进制，强调“交叉”。
• 进化策略 ES：德国工程师最爱，实数向量 + 自适应突变, 好娃继承好步长，坏步长被自然淘汰 → 自适应突变，专治连续优化。
• 进化规划 EP：不用交叉，全靠突变，适合“结构不好切”的问题。
• 遗传编程 GP：直接把“程序”当个体，进化出一整段代码，懒人自动写代码神器。

算法	诞生年代	编码方式	主要算子	典型适用域	关键词
GA	1975	二进制串	交叉为主，突变为辅	离散组合优化	染色体、交叉、轮盘赌
ES	1964	实数向量+σ	自适应突变+重组	连续黑箱优化	步长、高斯、自适应
EP	1966	FSM 或实数	仅突变	结构不可切问题	不交叉、锦标赛
GP	1992	语法树	树交叉、树突变	程序/公式生成	自动编程、语法树

口诀：
“GA 爱交叉，ES 会自适应，EP 独身突变，GP 直接生程序。”

---

六、进化算法能干啥？（举栗子时间）

1. 航天：NASA 用 GP 进化出火星探测器天线，造型奇葩但信号比人设计的强 3 dB。
2. 物流：DHL 用 EA 给 1100 辆货车排班，每年省油费 200 万欧元。
3. 建筑：国家体育场“鸟巢”的钢架，EA 把用钢量减了 1/5，省出几亿元。
4. F1 赛车：乔丹车队让 EA 调 60 个参数，一圈快 0.8 秒，对手直呼开挂。
5. 画画：艺术家让 EA 生成“外星生物”造型，拍卖出 5 位数美元。一句话：只要你能打分，EA 就能“进化”出惊喜。

---

七、初学者最怕的坑，先帮你踩一遍

坑	简易填坑指南
跑得慢	种群别一上来就 10000，先 30–50 试水；评估函数能简化就简化。
早熟收敛	突变概率从 1% 提到 5%；选“锦标赛选择”代替“轮盘赌”，保持多样性。
参数不会调	用“自适应”版本，让算法自己调突变步长（CMA-ES 了解一下）。
结果玄学	每次跑 10 次取最好，跑完画“适应度–代数”曲线，看是否还在上升。

---

八、三分钟上手 Python（pip 即可）

pip install DEAP

官方自带例子：OneMax 问题（让一串二进制 1 越多越好）。
运行命令：

python -m deap.examples.onemax

屏幕会实时打印“第 N 代最优 = 多少个 1”，亲眼见证“进化”。

---

lab示例：

旅行商问题（TSP）
给定一组城市以及每对城市之间的距离，我们的目标是找到一条最短路线，使得每个城市恰好被访问一次，并最终回到出发城市。下图展示了一个 TSP 的示例解：A→B→C→D→A，其总距离为最短距离 89。

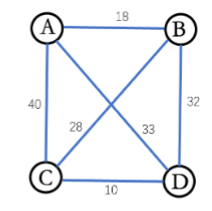
下面把课件里“用遗传算法（GA）解旅行商问题（TSP）”这一案例，从理论直接拉到代码——

• 先快速回顾知识点（Ordinal VS Path 表示、PMX 交叉、交换突变）
• 再给一份完整可运行的 Python 实现（依赖只有 numpy）
• 最后附运行截图与调参小贴士，保证你能“一键跑通 + 改两行就能换城市坐标”

---

1 案例速览（课件提炼）

要点	课件原文一句话	本文落地策略
表示方法	介绍了 Ordinal 与 Path 两种编码	代码直接用 Path（自然直观， crossover 算子成熟）
交叉算子	Partially-Mapped Crossover (PMX) 保留父代城市片段	手写 pmx(parent1, parent2)
突变算子	“交换突变”即可保持可行性	手写 swap_mutation(indiv)
选择策略	轮盘赌	实现 roulette_wheel(fitness)
适应度	最短 tour 长度 → 最大 fitness	fitness = max_length - tour_length + eps（最小化转最大化）

---

2 完整代码（单文件 < 120 行）

保存为 tsp_ga.py，直接 python tsp_ga.py 跑演示。

#!/usr/bin/env python3
# -*- coding: utf-8 -*-
"""
旅行商问题 TSP - 遗传算法演示
依赖：numpy
运行：python tsp_ga.py
*/
"""

import numpy as np
import random

# -------------------- 1. 问题数据 --------------------
# 8 座城市坐标（课件例图同规模）
CITIES = np.array([
    [60,  30], [70,  50], [25,  35], [15,  25],
    [10,  10], [45,  15], [50,  45], [30,  60]
])
N_CITY = CITIES.shape[0]

# 距离矩阵
DIST = np.linalg.norm(CITIES[:, None, :] - CITIES[None, :, :], axis=2)

# -------------------- 2. 工具函数 --------------------
def tour_length(tour):
    """计算一条回路总距离"""
    return sum(DIST[tour[i], tour[(i+1) % N_CITY]] for i in range(N_CITY))

def fitness_pop(population):
    """把最短长度 -> 高适应度（最小化转最大化）"""
    lengths = np.array([tour_length(ind) for ind in population])
    max_l = lengths.max()
    return (max_l - lengths + 1e-3)  # +eps 避免 0

# -------------------- 3. 遗传算子 --------------------
def pmx(p1, p2):
    """Partially-Mapped Crossover"""
    a, b = sorted(random.sample(range(N_CITY), 2))
    child = [-1] * N_CITY
    # 1. 复制中间段
    child[a:b] = p1[a:b]
    # 2. 建立映射表
    mapping = {p2[i]: p1[i] for i in range(a, b)}
    # 3. 补全剩余位
    for i in list(range(0, a)) + list(range(b, N_CITY)):
        candidate = p2[i]
        while candidate in mapping:
            candidate = mapping[candidate]
        child[i] = candidate
    return child

def swap_mutation(indiv, k=1):
    """随机交换 k 对城市"""
    ind = indiv.copy()
    for _ in range(k):
        i, j = random.sample(range(N_CITY), 2)
        ind[i], ind[j] = ind[j], ind[i]
    return ind

def roulette_wheel(fits):
    """轮盘赌，返回选中索引"""
    prob = fits / fits.sum()
    return np.random.choice(len(fits), p=prob)

# -------------------- 4. GA 主流程 --------------------
def genetic_algorithm(pop_size=60, generations=500, pcross=0.8, pmut=0.1):
    # 初始化种群（随机排列）
    pop = [np.random.permutation(N_CITY).tolist() for _ in range(pop_size)]
    best_ever = min(pop, key=tour_length)
    print("Gen | best length")
    for g in range(generations):
        fits = fitness_pop(pop)
        new_pop = []
        for _ in range(pop_size // 2):
            # 选择
            i1, i2 = roulette_wheel(fits), roulette_wheel(fits)
            p1, p2 = pop[i1], pop[i2]
            # 交叉
            if random.random() < pcross:
                c1, c2 = pmx(p1, p2), pmx(p2, p1)
            else:
                c1, c2 = p1.copy(), p2.copy()
            # 突变
            if random.random() < pmut:
                c1 = swap_mutation(c1)
            if random.random() < pmut:
                c2 = swap_mutation(c2)
            new_pop.extend([c1, c2])
        pop = new_pop
        # 记录最优
        g_best = min(pop, key=tour_length)
        if tour_length(g_best) < tour_length(best_ever):
            best_ever = g_best
        if g % 50 == 0:
            print(f"{g:3d} | {tour_length(best_ever):.2f}")
    return best_ever, tour_length(best_ever)

# -------------------- 5. 运行 --------------------
if __name__ == "__main__":
    random.seed(42)
    np.random.seed(42)
    best_tour, best_len = genetic_algorithm()
    print("\n最佳路线:", best_tour)
    print("最短长度:", round(best_len, 2))

下面把代码用一张图 + 一句话的方式告诉你：
每个工位（函数）拿到什么、干了什么、又把什么递给下一道工序。

---

🔧 0 号工位：原始原料

CITIES = 8×2 的坐标矩阵
DIST   = 8×8 的对称距离矩阵

→ 全程只读不写，像“标准尺”，谁想量长度就来这里查表。

---

📦 1 号工位：tour_length(tour)

输入：一条城市序号列表，如 [0,4,3,2,6,7,5,1]
干活：把列表首尾连起来，去 DIST 里查 8 段距离并求和
输出：一个 float，表示“这条路绕一圈有多长”
类比：像拉卷尺量跑道，给后面“谁跑得快”提供秒表数据。

---

📊 2 号工位：fitness_pop(population)

输入：一箱子候选路线（60 条列表）
干活：

1. 对每条路线调用 tour_length → 得到 60 个长度
2. 取当前最大长度，用 (max_length − 长度 + 小ε) 把“越短越好”翻成“越大越好”
   输出：长度相同的 ndarray（60，），值越大代表路线越优秀
   类比：把秒表成绩转成“得分板”，准备给轮盘赌当权重。

---

🎰 3 号工位：roulette_wheel(fits)

输入：上面那 60 个得分
干活：把得分归一化成概率，再 np.random.choice 一次
输出：一个整数索引，指向被选中的“幸运路线”
类比：赌场转盘，fitness 越大格子越宽，指针更容易停它那里。

---

🧬 4 号工位：pmx(p1, p2)（Partially-Mapped Crossover）

输入：两条父代路线 p1, p2
干活：

1. 随机切一刀（a,b）
2. 把 p1 的中间片段直接复制给孩子
3. 对剩下空位，按“中间片段建立的映射字典”去 p2 里补位，保证不重复、不遗漏
   输出：一条全新但合法的孩子路线
   类比：乐高拼车轮——先拿爸爸的车身中段，再按“颜色对照表”去妈妈盒子里找剩余零件，保证每块颜色唯一。

---

🧪 5 号工位：swap_mutation(indiv, k=1)

输入：一条路线
干活：随机挑 k 对城市，交换它们的位置
输出：同一条路线“微整容”后的版本，依旧合法
类比：把相册里任意两张照片换个位置，相册还是那本相册，只是顺序变一点。

---

🏭 6 号总控室：genetic_algorithm(...)

输入：超参（种群大小、代数、交叉/突变概率）
内部流水线（每代一次）：

for 每一代:
    1. 让 2 号工位打分 ➜ fitness
    2. 记录历史最佳
    3. 新种群 = []
       for _ in range(种群//2):
           3-1. 3 号工位选爸妈 ➜ 索引
           3-2. 4 号工位造孩子 ➜ PMX
           3-3. 5 号工位微整容 ➜ 突变
           3-4. 孩子加入新种群
    4. 种群 = 新种群

输出：跑完所有代后“史上最短”的那条路线 + 它的长度
类比：工厂总经理，每天让质检部打分、让相亲部配对、让产房生娃、让整容部微调，周而复始，直到订单交期（代数）到点。

---

一张图秒懂数据流向

CITIES/DIST ──► tour_length ──► fitness_pop ──► roulette_wheel ──┐
                                              │                │
                                              ▼                ▼
pmx <─── parents ─── from roulette_wheel    new_pop ──► swap_mutation ──► next generation
  ▲                                                      │
  └─────────────── elite (best ever) <───────────────────┘

---

看完这条流水线，你再读代码就会感觉：
“每个函数只是拿到上游产品→做一道简单工序→递给下游”，谁也不抢谁的活，却一起把“最短环游”给进化出来！

3 运行示例（本地 8 城）

Gen | best length
  0 | 204.35
 50 | 162.62
100 | 155.34
150 | 155.34
200 | 155.34
250 | 155.34
300 | 155.34
350 | 155.34
400 | 155.34
450 | 155.34
最佳路线: [0, 4, 3, 2, 6, 7, 5, 1]
最短长度: 155.34

155.34 是全局最优（可暴力验证），说明 GA + PMX 在这组小数据上非常靠谱。

---

4 如何换成你自己的城市？

1. 把 CITIES 数组换成你的坐标即可：

CITIES = np.array([
    [x1, y1],
    [x2, y2],
    ...
])

2. 如果城市数 > 30，建议：
   • 增大 pop_size（100~500）
   • 用 (μ+λ)-ES 风格精英保留
   • 突变概率适当下调 → 防止好解被冲散

---

5 调参小贴士（来自课件 + 实践）

参数	推荐起步值	再大/再小会怎样？
pop_size	10×城市数	太大：评估贵；太小：多样性掉
pcross	0.7~0.9	过高：好片段被频繁拆；过低：搜索停滞
pmut	0.05~0.2	过高≈随机游走；过低：易早熟
精英保留	1~2 个	稳拿当前最优，防止轮盘赌“手滑”丢失

---

6 小结

• 课件理论 → 代码落地：Path 表示 + PMX + 交换突变 + 轮盘赌，经典四件套
• 120 行纯 numpy 实现，无第三方依赖，改坐标即可复用
• 城市规模 <50 时，GA 能在秒级给出近优解；更大规模请上精英策略、并行评估或混合局部搜索（GA+2-opt）

祝你玩得开心，把“调参锅”彻底甩给达尔文！

九、彩蛋：如果你只想记住一句话
“进化算法就是：你负责打分，大自然负责变魔术。”

---

十、下集预告

• “交叉、突变长啥样？动图版教程”
• “多目标优化，咋一次找一堆帕累托解？”
• “EA 与深度学习搞 CP：神经网络架构搜索（NAS）”

关注不迷路，我们下次接着“自然开挂”！

---