EdgeMark：嵌入式人工智能工具的自动化与基准测试系统

Wang X, Jia W. Optimizing edge AI: a comprehensive survey on data, model, and system strategies[J]. arXiv preprint arXiv:2501.03265, 2025.

1. 引言与背景

人工智能技术的快速发展正在从根本上改变数据处理和分析的方式。传统的AI系统主要依赖云计算平台，利用其强大的计算资源进行复杂的模型训练和推理。然而，随着物联网设备的普及和边缘计算需求的增长，将AI能力直接嵌入到资源受限的设备中变得越来越重要。这种被称为嵌入式人工智能（embedded AI, eAI）或微型机器学习（TinyML）的范式，正在推动从智能家居、可穿戴设备到工业自动化和医疗保健等领域的创新。

嵌入式AI面临的核心挑战在于如何在极其有限的硬件资源下实现有效的机器学习推理。典型的微控制器可能只有几百KB的RAM和几MB的Flash存储，而现代深度学习模型动辄需要几百MB甚至GB级别的内存。这种资源差距促使研究人员开发了各种专门的工具和技术，包括模型量化、剪枝、知识蒸馏等优化方法。

本研究提出的EdgeMark系统旨在解决eAI工具选择和部署中的关键问题。通过提供自动化的工作流程和全面的基准测试，EdgeMark帮助开发者在众多可用工具中做出明智的选择，并简化从模型开发到嵌入式部署的整个过程。

2. eAI工具生态系统详细分析

2.1 TensorFlow Lite Micro (TFLM) 深度剖析

TFLM的设计理念基于内核抽象层，允许不同硬件供应商为其特定架构提供优化实现。这种架构使得TFLM能够在保持通用性的同时，充分利用特定硬件的加速能力。例如，ARM提供的CMSIS-NN库为Cortex-M系列处理器提供了高度优化的神经网络内核，利用SIMD指令实现了显著的性能提升。

TFLM的内存管理采用静态分配策略，所有张量缓冲区都在编译时确定大小。Arena大小的计算基于以下原理：

$$\text{Arena Size}=\underset{i}{\max }\left({\text{Input}}_i+{\text{Output}}_i+{\text{Temp}}_i\right)$$

其中$i$遍历模型的所有层，${\text{Input}}_i$、${\text{Output}}_i$和${\text{Temp}}_i$分别表示第$i$层的输入、输出和临时缓冲区大小。

2.2 Edge Impulse平台架构

Edge Impulse采用云端协同的架构，将模型训练和优化放在云端进行，而推理则在边缘设备上执行。平台的EON编译器是其核心创新之一，它通过消除解释器开销来减少内存使用。EON编译器的工作原理是将TensorFlow Lite模型直接转换为C++代码，生成的代码包含了所有必要的张量操作和内存管理逻辑。

该平台支持的信号处理模块包括快速傅里叶变换（FFT）、梅尔频率倒谱系数（MFCC）等，这些预处理步骤对于音频和振动数据的分析至关重要。

2.3 Ekkono的增量学习机制

Ekkono的独特之处在于其支持设备上的增量学习。这种能力通过以下机制实现：

$${\theta }_{t+1}={\theta }_t-\alpha {\nabla }_{\theta }L(x_t,y_t;{\theta }_t)$$

其中${\theta }_t$是时间$t$的模型参数，$\alpha$是学习率，$L$是损失函数，$(x_t,y_t)$是新的数据样本。这种在线学习方法使得模型能够适应环境变化，而无需重新训练整个模型。

2.4 硬件特定优化：Renesas eAI Translator

Renesas eAI Translator针对RX系列微控制器的特定架构进行了深度优化。该工具能够识别RXv2架构的特殊指令集，如DSP扩展和浮点单元，并生成相应的优化代码。例如，对于矩阵乘法操作，它可以生成利用MAC（乘累加）指令的高效实现。

3. EdgeMark系统架构与实现细节

3.1 模块化设计理念

EdgeMark采用分层模块化架构，每个模块负责工作流程中的特定阶段。这种设计带来了几个关键优势：模块间的松耦合使得系统易于维护和扩展；标准化的接口定义使得新工具的集成变得简单；并行处理能力允许同时处理多个模型。

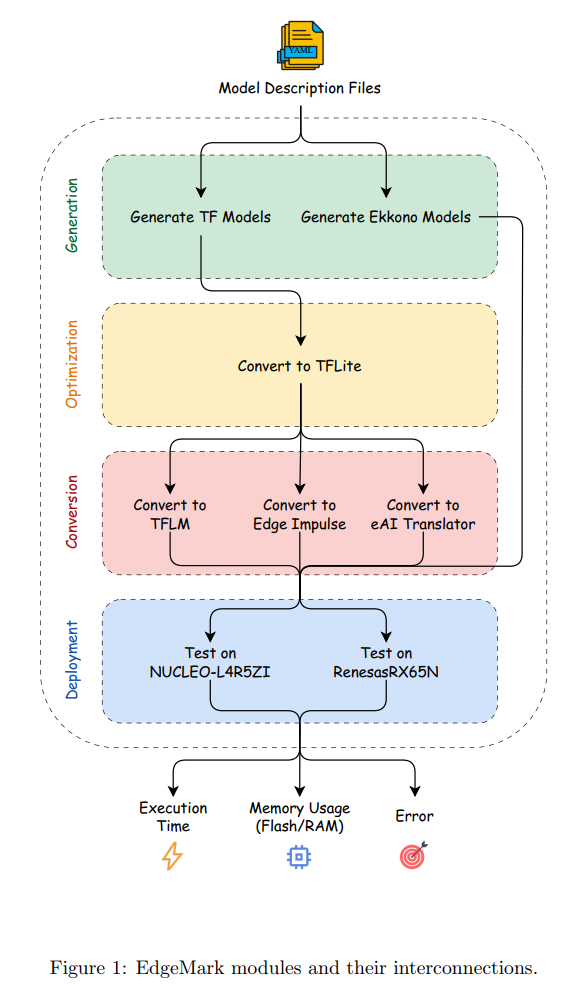
图1描述：EdgeMark模块架构图展示了系统的四个主要功能块：生成（Generation）、优化（Optimization）、转换（Conversion）和部署（Deployment）。图中显示了数据流从顶部的YAML配置文件开始，经过各个处理模块，最终产生执行时间、内存使用和部署误差等性能指标。各模块之间的箭头表示数据依赖关系，虚线框表示功能块的逻辑分组。

3.2 自动化工作流程

EdgeMark的自动化流程包括以下关键步骤：

模型生成阶段：系统解析YAML配置文件，构建TensorFlow计算图。配置文件支持灵活的模型定义，例如卷积层参数[channels, kernel_size, stride]的三元组表示法。

优化阶段：系统应用多种优化技术。量化过程使用以下映射函数：

$$q=\text{round}\left(\frac{r-z}{s}\right)$$

其中$r$是实数值，$q$是量化值，$z$是零点，$s$是缩放因子。反量化过程为：

$$r^{\prime }=s\cdot q+z$$

转换阶段：不同工具的转换策略各不相同。TFLM生成包含模型权重的C++数组和执行图的代码；Edge Impulse的EON编译器生成无解释器的直接执行代码；eAI Translator生成利用硬件特定优化的C代码。

3.3 Arena Size优化算法的数学基础

EdgeMark实现的Arena Size搜索算法基于二分搜索的变体，但加入了自适应步长调整机制。算法的收敛性可以通过以下不等式证明：

$$|A_{n+1}-A^{\ast }|\le \rho \cdot |A_n-A^{\ast }|$$

其中$A_n$是第$n$次迭代的arena size估计，$A^{\ast }$是最优值，$\rho <1$是收敛率。当使用二分搜索时，$\rho =0.5$，保证了对数时间复杂度$O(\log N)$。

4. 综合基准测试与性能分析

4.1 实验设计与模型选择

实验设计遵循了严格的科学方法，确保结果的可重复性和统计显著性。模型选择覆盖了广泛的复杂度范围，从简单的线性模型到复杂的深度网络。

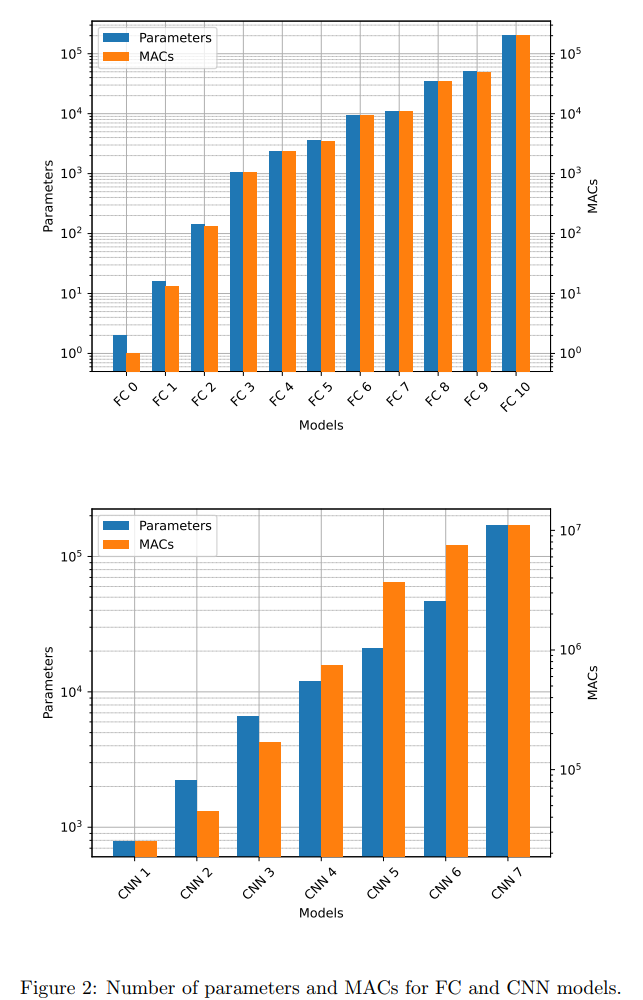
图2描述：该图展示了FC和CNN模型的参数数量和MACs（乘累加操作）分布。上方子图显示FC模型从FC 0到FC 10的分布，使用双对数坐标系，蓝色条形表示参数数量，橙色条形表示MACs。下方子图展示CNN模型的类似信息。可以看到模型复杂度呈现良好的梯度分布，FC模型的参数范围从$10^0$到$10^5$，MACs从$10^0$到$10^5$；CNN模型的参数范围从$10^3$到$10^5$，MACs从$10^5$到$10^7$。

4.2 量化技术的深入分析

量化是减少模型大小和加速推理的关键技术。不同量化方案的数学基础和性能影响如下：

动态范围量化：权重在部署时量化为int8，但激活保持float32。这种方案的量化误差可以表示为：

$${ϵ}_w=\frac{\max (W)-\min (W)}{2^8-1}$$

全整数量化（Int8）：权重和激活都量化为8位整数。量化误差的期望值为：

$$E[{ϵ}^2]=\frac{s^2}{12}$$

其中$s$是量化步长。

混合精度量化（16x8）：激活使用16位，权重使用8位。这种方案在精度和效率之间取得平衡，特别适合对激活范围变化较大的模型。

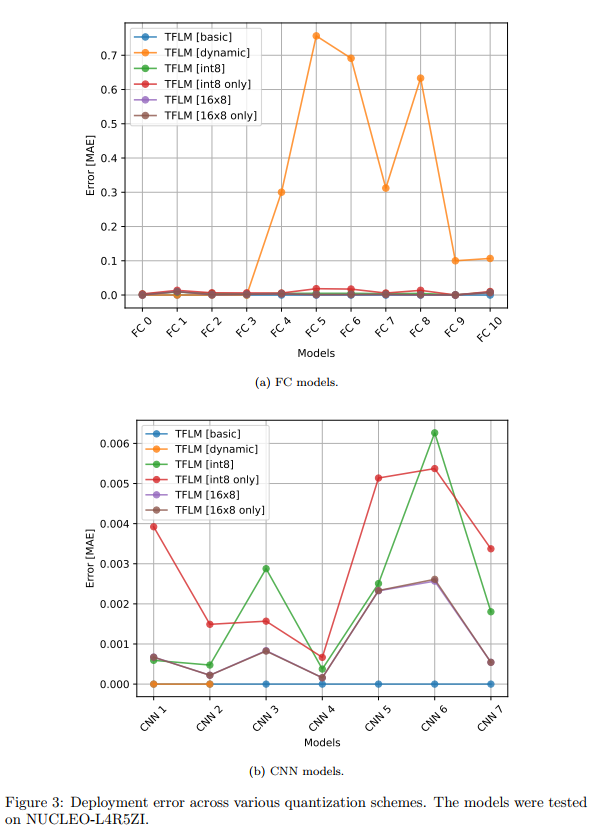
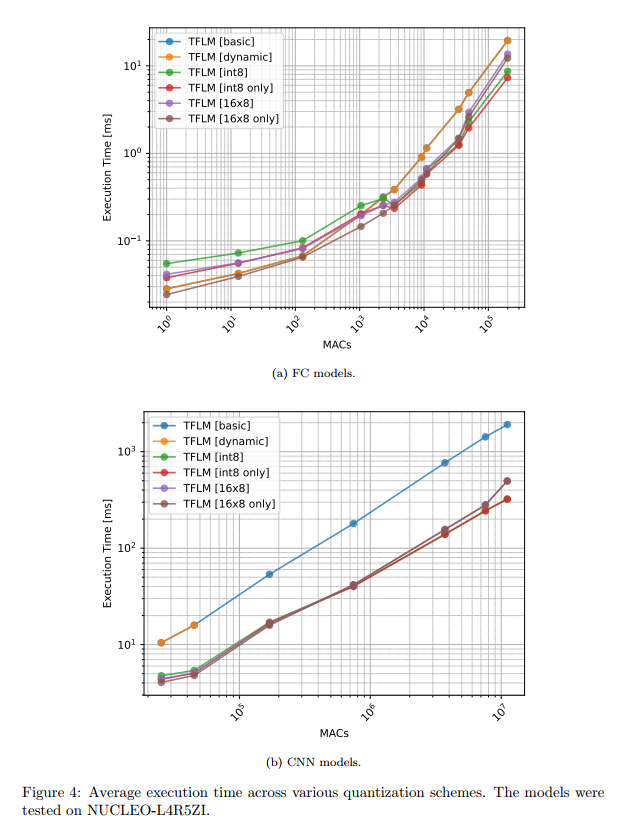
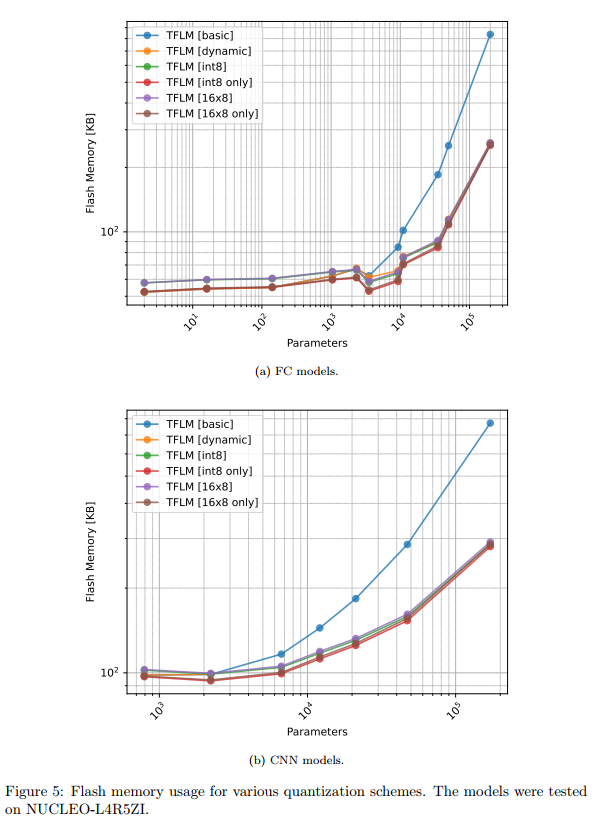
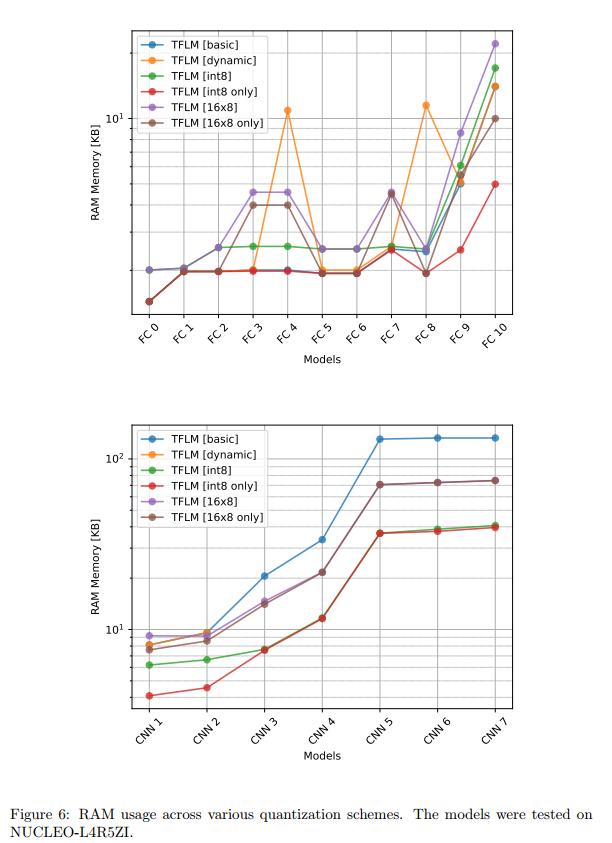
图3-6描述：这组图表展示了不同量化方案在STM32板上的性能比较。图3显示部署误差，可以看到动态量化在某些模型上产生了高达0.7的MAE误差，而其他量化方案的误差都在0.01以下。图4的执行时间对比显示，对于CNN模型，使用CMSIS-NN优化的int8量化比基础版本快约10倍。图5和图6分别展示了Flash和RAM使用情况，量化版本在大模型上可以节省75%的Flash空间。

4.3 工具对比的定量分析

通过大规模的实验，我们得出了以下定量结论：

TFLM vs Edge Impulse：在执行时间方面，TFLM在小型FC模型上平均快15-20%。但Edge Impulse在Flash使用上更高效，基础库大小仅为TFLM的60%左右。

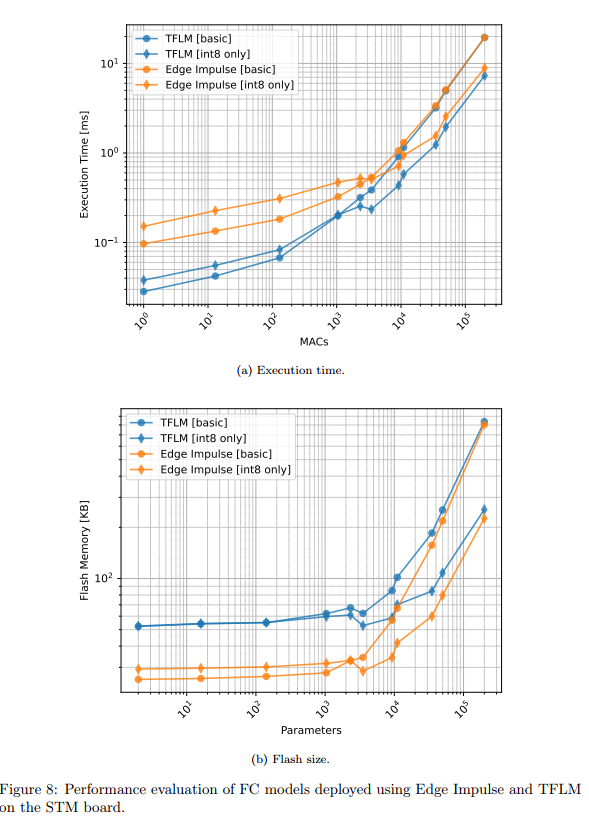
图8描述：该图展示了FC模型在STM板上使用TFLM和Edge Impulse的性能对比。执行时间子图使用双对数坐标，显示两种工具的执行时间随MACs增加的变化趋势。Flash大小子图显示Edge Impulse在小模型上的优势更明显，但随着模型增大，差距逐渐缩小。

TFLM vs Ekkono：Ekkono的轻量级设计使其在小模型上表现出色，基础库仅18.8KB，而TFLM需要52.2KB。但对于参数超过10,000的模型，TFLM的int8量化版本在所有指标上都优于Ekkono。

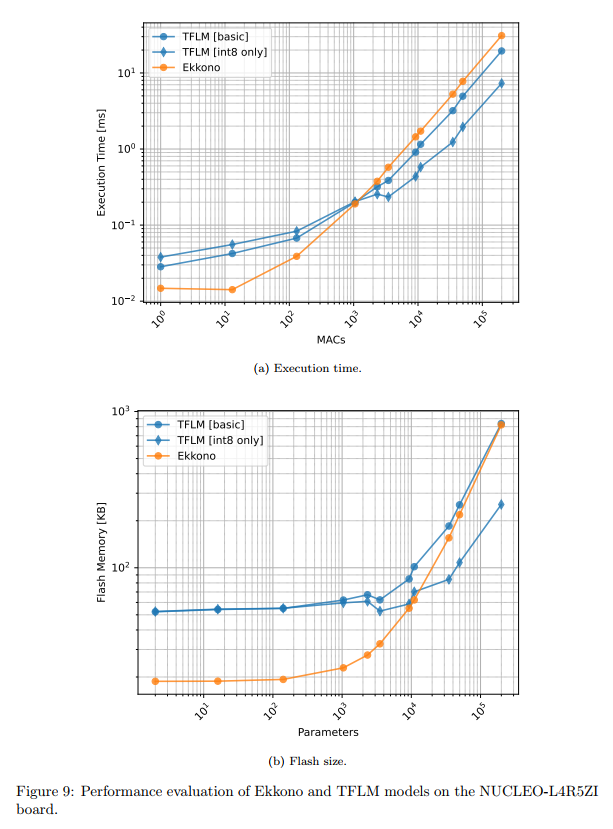
图9描述：该图对比了Ekkono和TFLM在NUCLEO-L4R5ZI板上的性能。执行时间图显示了一个交叉点，约在$10^3$ MACs处，在此之前Ekkono更快，之后TFLM占优。Flash大小图展示了类似的趋势。

4.4 硬件相关性分析

不同硬件平台对工具性能有显著影响。STM32的ARM Cortex-M4架构受益于CMSIS-NN优化，而Renesas的RXv2架构则通过专有优化获得性能提升。

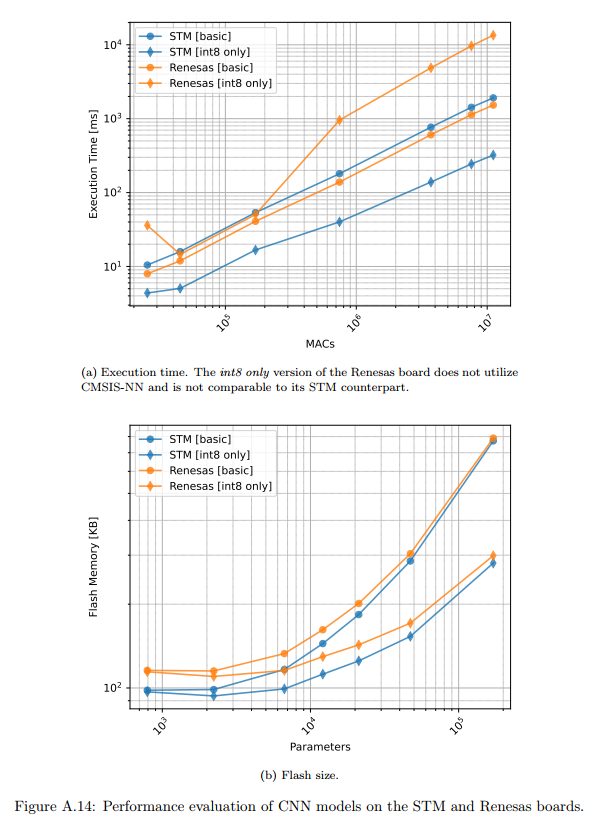
图14描述：该图比较了CNN模型在STM和Renesas板上的性能。执行时间子图显示，在没有使用CMSIS-NN优化的情况下，Renesas板略快。Flash大小子图表明STM板的内存效率更高，这主要归因于编译器和库的差异。

5. 实验结果的深入讨论

5.1 量化策略的选择准则

基于实验结果，我们提出以下量化策略选择准则：

对于内存极度受限的场景（Flash < 100KB），应优先选择int8 only量化，它能将模型大小减少约75%，同时保持可接受的精度损失（典型MAE < 0.01）。

对于需要更高精度的应用，16x8量化提供了良好的折中。虽然内存使用比int8高约50%，但精度提升明显，特别是在处理动态范围大的数据时。

对于计算资源充足但需要最高精度的场景，保持float32精度可能是必要的，尽管这会导致4倍的内存使用和显著的性能下降。

5.2 工具选择的多维度考虑

选择合适的eAI工具需要考虑多个维度：

开发效率：Edge Impulse提供了最友好的用户界面和完整的端到端工作流程，适合快速原型开发。其云端训练和自动优化功能大大降低了开发门槛。

性能优化：对于需要极致性能的应用，供应商特定的工具如STM32Cube.AI或Renesas eAI Translator通常能提供最佳性能，因为它们能充分利用硬件特性。

灵活性与可移植性：TFLM提供了最好的跨平台支持，其基于内核的架构使得同一模型可以在多种硬件上运行，虽然可能牺牲一些性能。

特殊功能需求：如果需要设备上学习能力，Ekkono几乎是唯一的选择。其增量学习功能使得模型能够适应环境变化，这在预测性维护等应用中非常有价值。

5.3 EdgeMark系统的实际应用价值

EdgeMark系统在实际应用中展现出了显著价值。通过自动化整个工作流程，开发时间从传统的数天缩短到数小时。系统的模块化设计使得新工具的集成变得简单，研究人员可以快速评估新技术的性能。

更重要的是，EdgeMark提供的标准化基准测试环境确保了结果的可比性和可重复性。这对于学术研究和工业应用都至关重要，因为它消除了由于测试环境差异导致的不确定性。

6. 结论与未来展望

本研究通过EdgeMark系统对嵌入式AI工具进行了全面的评估和比较。主要贡献包括：提供了现有eAI工具的综合评述，揭示了它们的优势和局限性；开发了开源的EdgeMark自动化系统，简化了从模型开发到嵌入式部署的整个流程；通过大规模实验提供了工具性能的定量比较，为选择合适的工具提供了数据支持。

研究结果表明，没有单一的"最佳"工具能够满足所有需求。不同的应用场景需要不同的权衡。TFLM的通用性使其成为多数项目的安全选择；Edge Impulse的易用性适合快速原型开发；供应商特定工具在目标硬件上能提供最佳性能；Ekkono的独特功能填补了设备上学习的空白。

附录A：剪枝和聚类的性能分析

A.1 非结构化剪枝的局限性

研究评估了50%稀疏度的剪枝和16个中心的聚类对模型性能的影响。实验结果揭示了一个反直觉的现象：在通用处理器上，非结构化剪枝并不能带来性能提升。

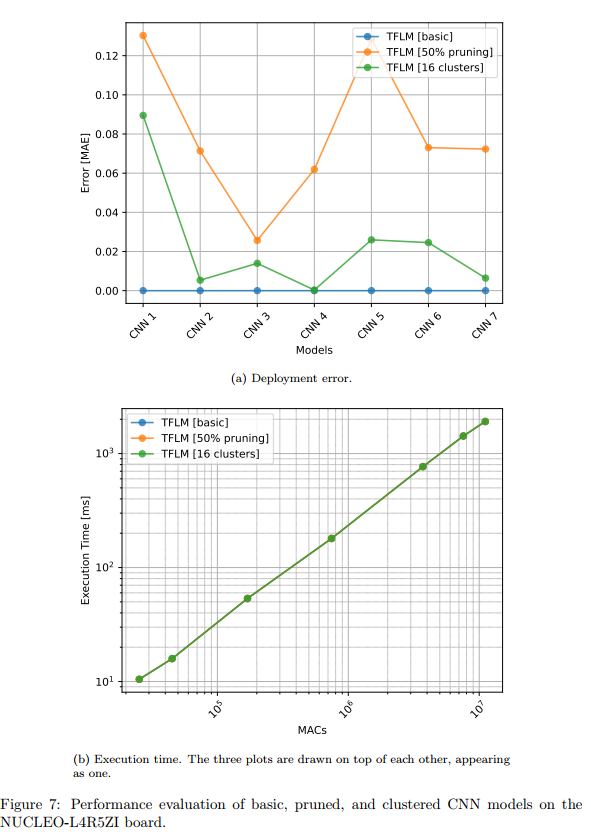
图7描述：该图展示了CNN模型在应用剪枝和聚类后的性能。上方子图显示部署误差从基础版本的接近0增加到剪枝版本的0.12。下方子图显示三条执行时间曲线完全重叠，表明剪枝和聚类对执行时间没有任何影响。

这一现象的根本原因在于硬件架构的限制。对于标量处理器，零值乘法和非零值乘法需要相同的时钟周期：

$$T_{pruned}=T_{original}=N\times t_{mult}$$

其中$N$是总操作数，$t_{mult}$是单次乘法的时间。即使50%的权重为零，处理器仍需要执行所有乘法操作。

A.2 RNN模型的特殊考虑

RNN模型的部署面临独特挑战。实验评估了SimpleRNN、LSTM和GRU模型，序列长度为100。

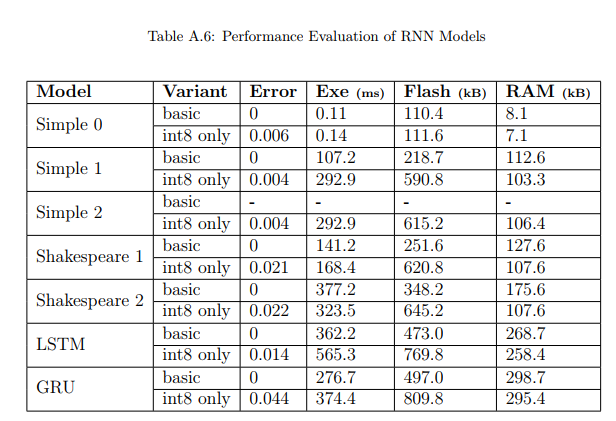
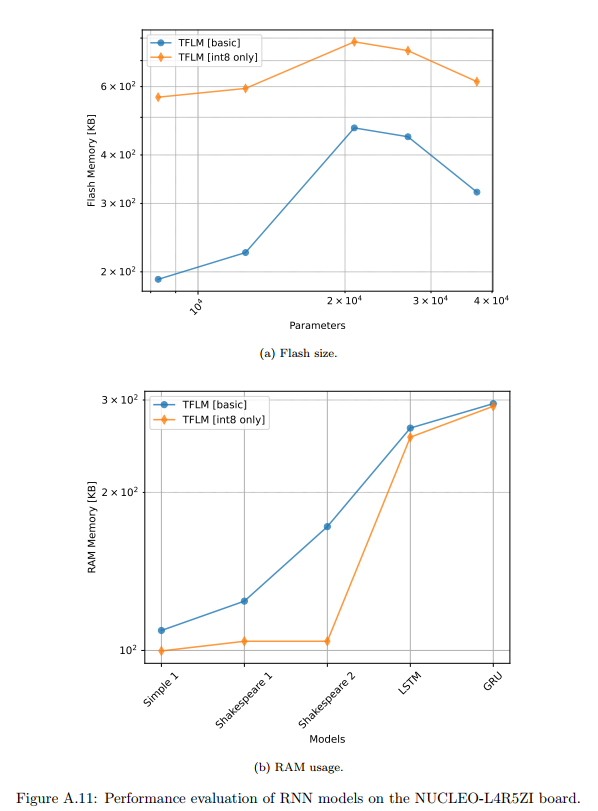
表A.6和图A.11描述：表格显示了RNN模型的详细性能数据。LSTM模型有26,912个参数和2,702,400个MACs，而GRU有20,896个参数和2,094,400个MACs。图A.11的Flash大小子图显示int8量化版本意外地需要更多Flash（约2-3倍），这与CNN模型的表现相反。RAM使用子图显示基础版本需要100-300KB的RAM，而int8版本略少。

RNN的内存使用可以表示为：

$$M_{RNN}=M_{weights}+T\times (M_{hidden}+M_{activation})$$

其中$T$是序列长度，$M_{hidden}$是隐藏状态大小，$M_{activation}$是激活内存。

A.3 编译器优化的影响

GCC编译器优化级别对性能有显著影响。实验比较了-O3（最大优化）、-Of（速度优化）和-Os（大小优化）。

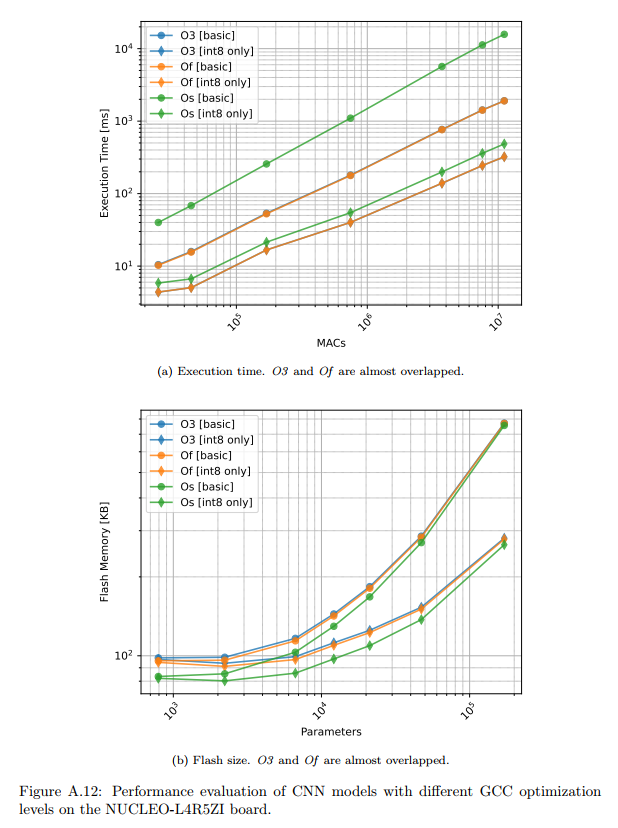
图A.12描述：该图展示了不同GCC优化级别下CNN模型的性能。执行时间图显示O3和Of几乎相同，都比Os快约20-30%。Flash大小图显示Os能节省5-10%的空间，但代价是性能下降。

优化的效果可以通过以下指标量化：

$$\text{Speedup}=\frac{T_{Os}}{T_{O3}}\approx 1.25$$

$$\text{Size Reduction}=\frac{S_{O3}-S_{Os}}{S_{O3}}\approx 0.08$$

A.4 浮点单元（FPU）的重要性

FPU对浮点运算密集型模型的性能至关重要。

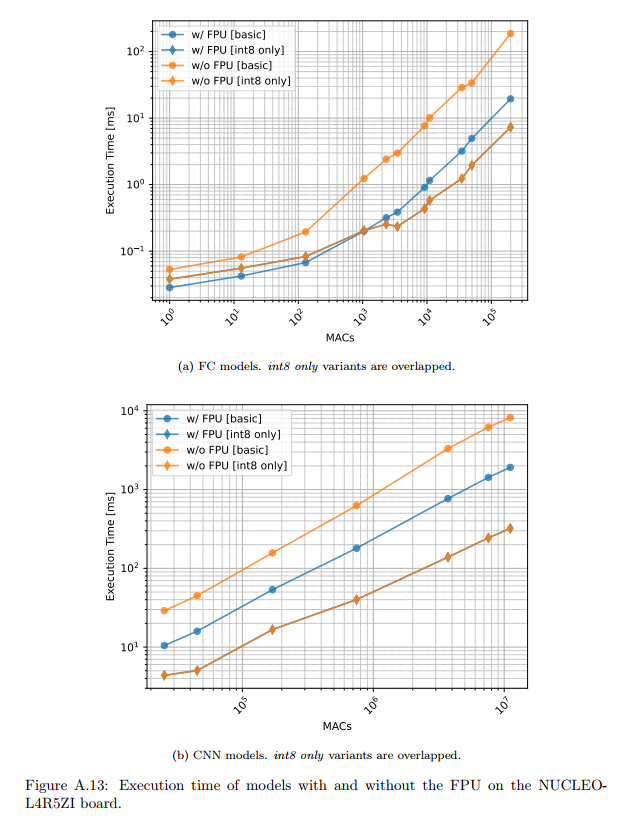
图A.13描述：该图对比了有无FPU时的执行时间。对于基础（float32）版本，FPU提供了85%到850%的加速，特别是在大型CNN模型上。然而，对于int8量化版本，由于使用整数运算，FPU的存在与否几乎没有影响，两条曲线完全重叠。

FPU加速可以建模为：

$${\text{Speedup}}_{FPU}=\frac{N_{float}\times (t_{soft}-t_{hard})}{T_{total}}+1$$

其中$N_{float}$是浮点操作数，$t_{soft}$和$t_{hard}$分别是软件和硬件浮点运算时间。

附录B：数学推导和理论基础

B.1 量化误差分析

量化过程引入的误差可以通过泰勒展开分析。设原始权重为$w$，量化后的权重为$\hat{w}$，量化误差为$ϵ=w-\hat{w}$。

对于线性层$y=wx+b$，量化后的输出为：

$$\hat{y}=\hat{w}x+\hat{b}=(w-{ϵ}_w)x+(b-{ϵ}_b)$$

输出误差为：

$$\Delta y=y-\hat{y}={ϵ}_{w}x+{ϵ}_b$$

误差的方差为：

$$\text{Var}(\Delta y)=\text{Var}({ϵ}_w)\text{Var}(x)+\text{Var}({ϵ}_b)$$

假设均匀量化，量化误差服从均匀分布$U(-\frac{s}{2},\frac{s}{2})$，则：

$$\text{Var}(ϵ)=\frac{s^2}{12}$$

B.2 Arena Size的理论下界

Arena size的理论下界可以通过图着色问题建模。将张量生命周期表示为区间图$G=(V,E)$，其中顶点$v_i\in V$表示张量，边$(v_i,v_j)\in E$当且仅当两个张量的生命周期重叠。

最小arena size等价于图的带权色数问题：

$${\chi }_w(G)=\underset{c:V\to C}{\min }\underset{k\in C}{\max }\sum _{v_i:c(v_i)=k}{w}_i$$

其中$w_i$是张量$i$的大小，$c$是着色函数。

对于链式结构的神经网络，这个问题可以简化为：

$$A_{min}=\underset{i}{\max }(S_{i-1}^{out}+S_i^{out}+S_i^{temp})$$

B.3 增量学习的收敛性证明

Ekkono的增量学习算法基于随机梯度下降。设损失函数$L(\theta )$是$\mu$-强凸的，梯度$\nabla L$是$L$-Lipschitz连续的。

则对于学习率$\alpha \le \frac{1}{L}$，算法的收敛速度为：

$$E[\Vert {\theta }_t-{\theta }^{\ast }{\Vert }^2]\le {\left(1-\frac{\mu }{L}\right)}^t\Vert {\theta }_0-{\theta }^{\ast }{\Vert }^2+\frac{\alpha {\sigma }^2}{\mu }$$

其中${\theta }^{\ast }$是最优参数，${\sigma }^2$是梯度噪声的方差。

这保证了算法的线性收敛率，收敛速度由条件数$\kappa =\frac{L}{\mu }$决定。

B.4 CMSIS-NN优化的理论加速比

CMSIS-NN通过SIMD指令实现加速。对于卷积操作，理论加速比为：

$$S_{SIMD}=\frac{T_{scalar}}{T_{SIMD}}=\frac{N\times t_{MAC}}{N/W\times t_{SIMD}+O_{overhead}}$$

其中$N$是总MAC操作数，$W$是SIMD宽度（ARM Cortex-M4为4），$O_{overhead}$是SIMD指令的额外开销。

在理想情况下（忽略开销），加速比接近SIMD宽度：

$$S_{SIMD}^{ideal}\approx W=4$$

实际测量显示，CMSIS-NN在CNN模型上实现了3.2-3.8倍的加速，接近理论上限。

B.5 内存带宽限制分析

对于内存受限的操作，性能受内存带宽$B$限制：

$$T_{mem}=\frac{D_{in}+D_{out}+D_{weights}}{B}$$

计算强度（Operational Intensity）定义为：

$$I=\frac{\text{FLOPs}}{\text{Memory Accessed}}$$

当$I<I_{critical}$时，性能受内存带宽限制；否则受计算能力限制。对于典型的微控制器：

$$I_{critical}=\frac{F_{compute}}{B_{memory}}\approx \frac{100\text{ MFLOPS}}{50\text{ MB/s}}=2$$

这解释了为什么某些模型的性能不随计算优化而线性提升。