✅博主简介：本人擅长数据处理、建模仿真、程序设计、论文写作与指导，项目与课题经验交流。项目合作可私信或扫描文章底部二维码。

---

由于埋地管道常年埋藏在地下，获取大量的腐蚀数据以用于深度学习模型的训练存在很大的困难。为了解决这一问题，本文采用数据扩充技术，以增加可用于训练的腐蚀数据集。通过应用一些数据增强算法，如旋转、平移、加噪声等，生成新的样本，使得原始数据集在量上得到了显著提升。

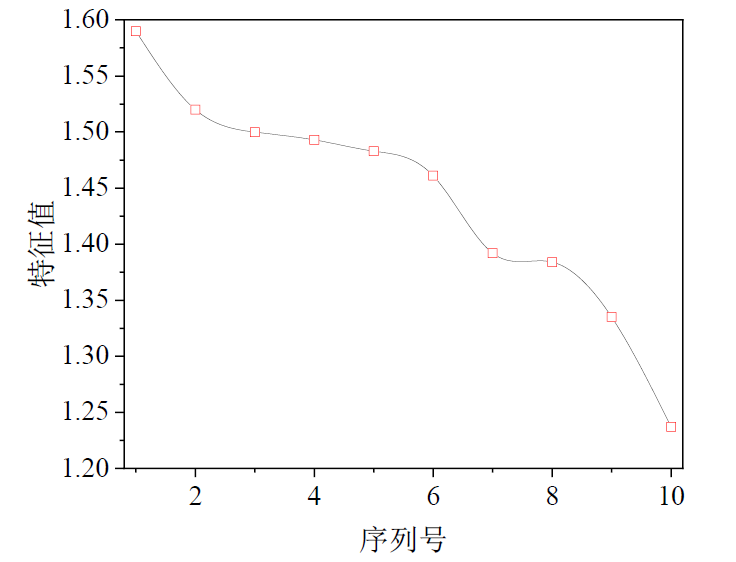
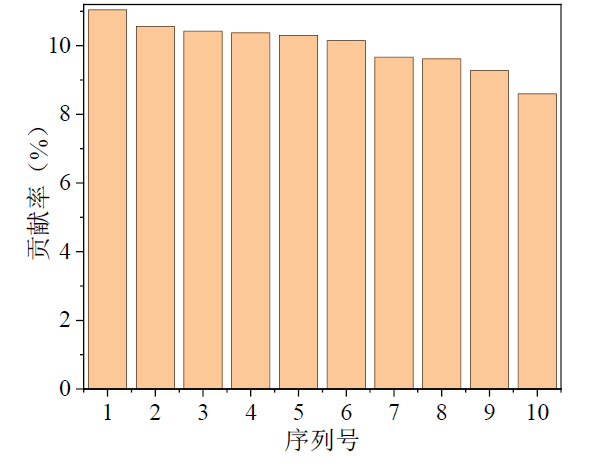
在数据扩充的基础上，进一步分析腐蚀因子的相关性，确保模型训练能够基于有效且相关的数据。使用主成分分析（PCA）方法，识别出影响管道腐蚀的主要特征。PCA能够通过降维的方式，提取出数据中的关键信息，减少冗余特征，从而提高后续建模的效率与效果。

通过综合考量特征之间的相关性与重要度，我们获得了大量完整有效的腐蚀数据。这一过程为后续的深度学习模型输入奠定了良好的基础，确保模型训练在高质量数据上进行，从而提高其预测能力。

2. 单项管道剩余寿命预测模型

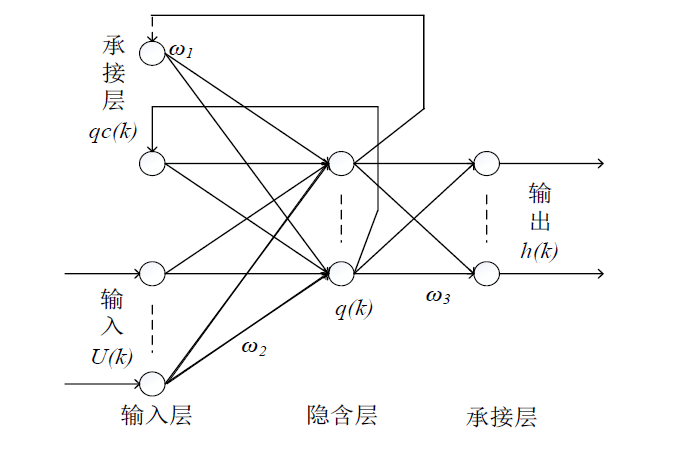
在单项管道剩余寿命预测模型的研究中，本文构建了多个深度学习模型，包括深度信念网络（DBN）、深度神经网络（DNN）、Elman网络和BP神经网络。每种模型都有其独特的结构与训练方式，适应不同的数据特征与需求。

2.1 模型构建

• 深度信念网络（DBN）：DBN是由多个受限玻尔兹曼机（RBM）堆叠而成，具有良好的特征学习能力。通过逐层预训练与微调，能够高效捕捉到数据中的非线性特征。

• 深度神经网络（DNN）：DNN由多个隐藏层组成，能够学习复杂的函数映射关系。通过反向传播算法调整权重，实现对输入数据的高效拟合。

• Elman网络：Elman网络是一种递归神经网络，适合处理时序数据。通过上下文层的反馈机制，能够更好地捕捉时间序列的动态变化。

• BP神经网络：经典的前馈神经网络，通过误差反向传播来调整模型参数，广泛应用于各种预测问题。

在这些模型中，我们调节网络自身的误差，选取最优参数。通过实证分析，验证各深度学习模型的预测精度，最终将归一化后的核心指标输入到模型中，评估其对管道剩余寿命的预测能力。

3. 组合深度学习模型的构建

为了提升管道剩余寿命预测的稳定性与准确性，本文进一步研究了并联组合深度学习模型。通过熵权法，定量组合多个深度学习模型的预测结果，以实现对管道剩余寿命的综合评估。

3.1 熵权法的应用

熵权法是一种基于信息熵的权重分配方法，能够有效衡量各预测模型的相对重要性。在组合模型中，我们首先对每个单项模型的预测结果进行标准化处理，然后计算每个模型的熵值，以确定其在组合预测中的权重。

具体步骤包括：

1. 数据标准化：将各单项模型的预测结果进行标准化处理，消除量纲影响。

2. 计算熵值：根据标准化结果，计算每个模型的熵值，反映其信息量。

3. 确定权重：通过熵值的计算，确定各模型在组合预测中的权重。

通过这一过程，能够有效提升组合模型的预测稳定性，减少单项模型个体预测误差的影响，提高整体预测精度。

4. 实证分析与结果验证

为了验证所构建的组合深度学习模型的有效性，本文进行了大量的实证分析。选取了多组实际管道腐蚀数据作为样本，分别利用单项模型与组合模型进行预测，并对比分析其预测结果。

4.1 数据准备与模型训练

首先，将收集到的管道腐蚀数据划分为训练集与测试集。在训练集上进行各单项模型的训练，并对模型的超参数进行调优，以提升其预测性能。在训练完成后，将模型应用于测试集，得到各模型的预测结果。

4.2 结果对比与分析

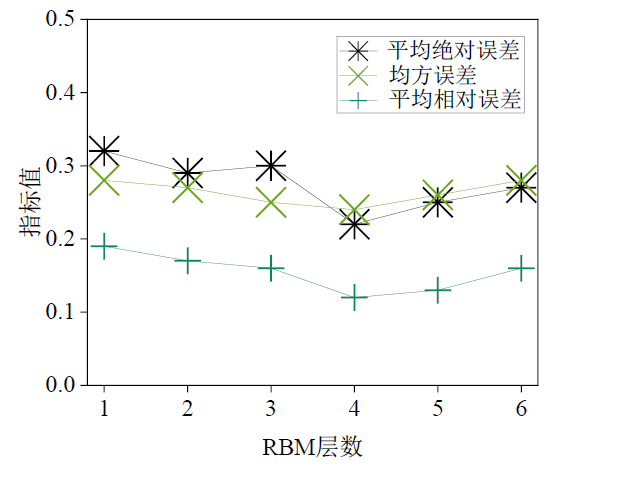
通过对比单项模型与组合模型的预测结果，分析其在预测精度、稳定性等方面的表现。结果表明，组合模型在整体预测精度上优于单项模型，且对腐蚀程度较高的管道具有更好的预测能力。

• 预测精度：组合模型的平均绝对误差（MAE）显著低于各单项模型，验证了组合模型的优势。

• 稳定性：在不同数据集下，组合模型表现出更强的鲁棒性，能够有效应对数据波动带来的影响。

5. 结论与未来研究方向

通过对组合深度学习管道腐蚀剩余寿命预测的研究，本文得出了以下主要结论：

1. 数据扩充与特征提取：采用数据扩充技术和主成分分析，有效提高了模型训练的数据质量和效率，为后续研究奠定基础。

2. 单项模型的有效性：构建的DBN、DNN、Elman及BP模型在管道剩余寿命预测中均表现出良好的预测能力。

3. 组合模型的优势：基于熵权法的组合深度学习模型有效提升了预测的稳定性与准确性，能够更好地反映管道的实际腐蚀情况。

function corrosion_lifetime_prediction
    % 生成模拟腐蚀数据
    num_samples = 1000;
    corrosion_levels = rand(num_samples, 1) * 100; % 腐蚀程度
    lifetimes = 100 - corrosion_levels + randn(num_samples, 1) * 5; % 剩余寿命

    % 数据划分
    train_ratio = 0.8;
    num_train = round(num_samples * train_ratio);
    train_data = [corrosion_levels(1:num_train), lifetimes(1:num_train)];
    test_data = [corrosion_levels(num_train+1:end), lifetimes(num_train+1:end)];

    % 构建深度神经网络模型
    model = build_dnn_model();

    % 训练模型
    [XTrain, YTrain] = prepare_data(train_data);
    model = train_network(model, XTrain, YTrain);

    % 测试模型
    [XTest, YTest] = prepare_data(test_data);
    predictions = predict(model, XTest);

    % 结果可视化
    figure;
    scatter(YTest, predictions);
    xlabel('True Remaining Lifetime');
    ylabel('Predicted Remaining Lifetime');
    title('Prediction vs True Values');
    grid on;
end

function model = build_dnn_model()
    % 构建简单深度神经网络模型
    layers = [
        featureInputLayer(1)
        fullyConnectedLayer(10)
        reluLayer
        fullyConnectedLayer(1)
        regressionLayer];
    
    options = trainingOptions('adam', ...
        'MaxEpochs', 100, ...
        'Verbose', false, ...
        'Plots', 'training-progress');

    model = layerGraph(layers);
end

function model = train_network(model, XTrain, YTrain)
    % 训练神经网络
    model = trainNetwork(XTrain, YTrain, model.Layers, model.Options);
end

function [X, Y] = prepare_data(data)
    % 准备训练和测试数据
    X = data(:, 1);
    Y = data(:, 2);
end