VAE

左图相当于变量x，右图相当于z

假如在AE中，一张满月的图片作为输入，模型得到的输出是一张满月的图片；一张弦月的图片作为输入，模型得到的是一张弦月的图片。当从满月的code和弦月的code中间sample出一个点，我们希望是一张介于满月和弦月之间的图片。但是，实际的结果是，生成图片是模糊且无法辨认的乱码图。因为我们并不知道模型从满月的code到弦月的code发生了什么变化。因为编码和解码的过程使用了深度神经网络，这是一个非线性的变换过程，所以在code空间上点与点之间的迁移是非常没有规律的。

对于一个生成模型而言，解码器部分应该是单独能够提取出来的，并且对于在规定维度下任意采样的一个编码，都应该能通过解码器产生一张清晰且真实的图片。

如何解决这个问题呢？我们可以引入噪声，使得图片的编码区域得到扩大，从而掩盖掉失真的空白编码点。

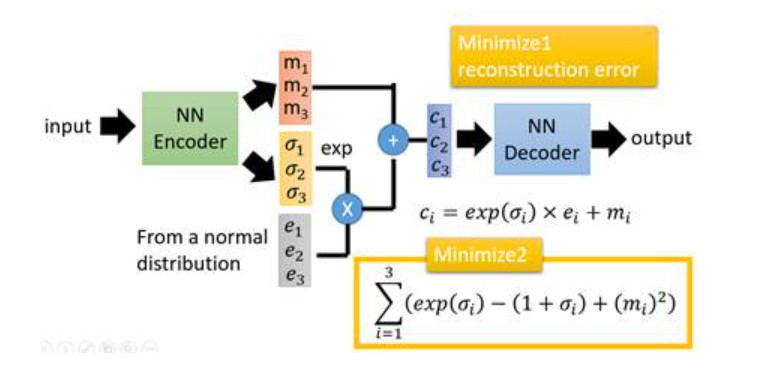
m对应原来AE中的code，$\sigma$是从输入图片中生成的，e是从正态分布中抽样得到的。

如上图所示，现在在给两张图片编码的时候加上一点噪音，使得每张图片的编码点出现在绿色箭头所示范围内，于是在训练模型的时候，绿色箭头范围内的点都有可能被采样到，这样解码器在训练时会把绿色范围内的点都尽可能还原成和原图相似的图片。然后我们可以关注之前那个失真点，现在它处于全月图和半月图编码的交界上，于是解码器希望它既要尽量相似于全月图，又要尽量相似于半月图，于是它的还原结果就是两种图的折中（3/4全月图）。

由此我们发现，给编码器增添一些噪音，可以有效覆盖失真区域。不过这还并不充分，因为在上图的距离训练区域很远的黄色点处，它依然不会被覆盖到，仍是个失真点。为了解决这个问题，我们可以试图把噪音无限拉长，使得对于每一个样本，它的编码会覆盖整个编码空间，不过我们得保证，在原编码附近编码的概率最高，离原编码点越远，编码概率越低。在这种情况下，图像的编码就由原先离散的编码点变成了一条连续的编码分布曲线，如下图所示。

VAE额外的损失函数

为什么要有？

因为如果不加的话，整个模型就会出现问题：为了保证生成图片的质量越高，编码器肯定希望噪音对自身生成图片的干扰越小，于是分配给噪音的权重越小，这样只需要将$({\sigma }_1,{\sigma }_2,{\sigma }_3)$赋为接近负无穷大的值就好了。就变回原来的AE了。

EM

KL散度