Python机器学习——决策树

决策树是什么？

决策树是一类常见的机器学习方法，决策顾名思义就是做决定，我们常说的if-else语句就是决策的判断的过程，每个决策或事件都可能引出两个或多个事件，导致不同的结果，把这种决策分支画成图形，就很像一棵树的枝干，故称**“决策树”**

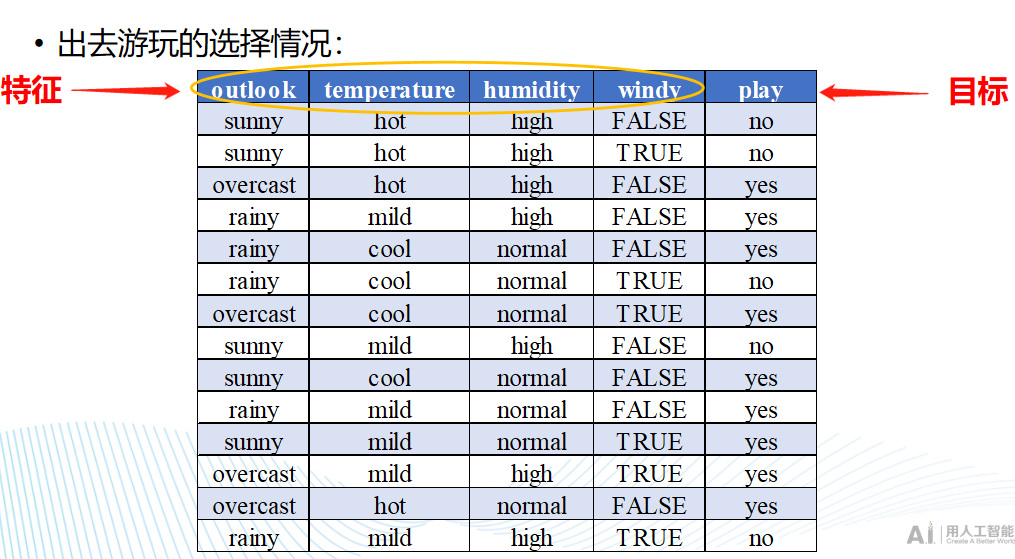
决策树在生活中很常见，举个出去游玩的例子吧

那么它就可以转换成一棵是否外出游玩的决策树

图中，矩形代表目标/类，椭圆代表属性或特征。

那么，决策树的构建就只有这些吗？

由此可以提出一些问题：

1. 是否所有的特征都要参与决策？
   • 选取哪些特征参与决策，哪些特征更重要？选取顺序如何确定？
   • 如果一不小心把重要的特征放在后面，前面是些不重要的特征，那么构建的决策树会很低效的
   • 例：利用决策树算法区分人和狗时，如果把眼睛、嘴巴、耳朵、鼻子数量等次要特征放在前面，而把是否会说话等重要特征放在后面，结果就是本来只需要一步决策就可以区分，而这样的算法必须执行很多步。
2. 如何根据特征以及其属性来生成决策树呢？(决策树生成问题)
   • 为什么决策树是这样的生长趋势，其他形状的决策树是否更为合适？
3. 如果选取的特征数过多，势必会造成过度学习(过拟合)，灵活性差，怎么办？(决策树剪枝问题)

由上面三大问题引出，决策树学习通常包括3个步骤:

特征选择：特征选择是指从训练数据中众多的特征中选择一个特征作为当前节点的分裂标准，如何选择特征有着很多不同量化评估标准标准，从而衍生出不同的决策树算法。

决策树生成： 根据选择的特征评估标准，从上至下递归地生成子节点，直到数据集不可分则停止决策树停止生长。 树结构来说，递归结构是最容易理解的方式。

剪枝：决策树容易过拟合，一般来需要剪枝，缩小树结构规模、缓解过拟合。剪枝技术有预剪枝和后剪枝两种。

决策树——特征选择

• 特征选择就是面对大量的特征如何选择合适的、重要的特征
• 因此需要有策略/指标来确定重要特征的选择

信息熵在信息论中有重要的作用，在图像处理中，也常作为图像压缩编码的重要运算标准

那什么是信息熵呢？

• 用以表示信息的不确定程度，信息越不确定，信息熵越大。信息越确定，信息熵越小
• 举几个例子：
  • 明天的太阳会从东边升起” ，无法获取新的信息，信息完全确定，熵=0
  • 如果天气预报分别说“明天有50%的可能性下雨” 和“明天有100%的可能性下雨”，很明显，第2句的信息量大，减小了不确定性（熵减少），获取到信息（信息增益）。
• 其实：获取信息（信息增益） = 消除熵（熵减少）
• 由此可见，信息熵是和概率有关的。

信息熵

信息熵的定义：

信息熵

• 通常以2或以e为底，单位称为比特（bit）或纳特（nat）
• 当所有的p_i相等时，熵最大，即不确定性最大，符合我们的认知
• 例：有ABCD四个选项，但不知道选哪个的时候，四个选项选的概率是一样的，不确定性是最大的
  • 一旦获取某一项的一些信息（C选项是错误的），不确定性就降低一些

• 当获知"选项C是错误的" 这个信息M，概率分布变为

  

• 那这个信息M带来的熵的变化(熵减少)为：

• 那这个信息M带来的熵的变化率为：

基尼指数

• 度量特征的不纯度（当所有叶子节点中的样本属于同一个类别，纯度最大，即足够纯，信息熵最小）
• 基尼指数越小，表示变量纯度越高，变量的不确定性越低
• 基尼指数越大，表示变量纯度越低，变量的不确定性越高
• 基尼指数，可以理解为对分类误差率的一种近似

那么说完衡量指标，应如何选取特征？

• 信息增益：特征的信息增益越大，意味着特征越重要——选取信息增益最大的特征
• 信息增益比：特征的信息增益比越大，意味着特征越重要——选取信息增益比最大的特征
• 基尼指数：特征的基尼指数越小，意味着特征的纯度越高——选取基尼指数最小的特征

决策树——决策树生成

对于决策树的生成，我们需要考虑以下几个问题：

• 如何从根节点开始来构造决策树？
• 在什么情况下树应该停止进一步的生长？
• 树如何对样本进行预测？
• 常用的算法有哪些
  • 信息增益：ID3算法
  • 信息增益比：C4.5算法
  • 基尼(Gini)指数：CART算法

简单了解一下这些算法的流程

ID3算法、C4.5算法

CART算法特点：一种二叉树、可以用于解决回归问题。

决策树——决策树剪枝

不同的决策树算法适用于不同的剪枝方式，常用的剪枝方式有先剪枝与后剪枝两种。

• 先剪枝：生成过程中，设置阈值，限制不必要的子树生成
• 后剪枝：先生成一棵最大树，然后再根据度量损失，进行剪枝

总结

通过对以上决策树知识点的学习，总结出决策树也同样优缺点并存

优点：

• 建立决策树模型的过程非常容易理解
• 决策树模型可以可视化，非常直观
• 可用于分类和回归，而且非常容易做多类别的分类
• 能够处理数值型和连续的样本特征

缺点：对噪声数据比较敏感，容易过拟合

决策树算法在工业中本身应用并不多，但很多算法都是以决策树为基础搭建出来的，包括随机森林、Adaboost、GBDT等等

理解决策树，是学习这些算法的基石