智源导读：深度学习的统计神经动力学主要涉及用信息几何的方法对深度随机权值网络进行研究。深度学习技术近年来在计算机视觉、语音识别等任务取得了巨大成功，但是其背后的数学理论发展却很滞后。日本理化所的Shun-ichi Amari先生（中文：甘利俊一）近期在北京智源大会上发表了题为《信息几何法：理解深度神经网络学习机制的重要工具》的演讲。在演讲中，甘利先生梳理了人工神经网络研究的部分重要历史事件，分享了近两年在深度学习理论的一些最新研究成果，指出统计神经动力学方法可以为理解深度学习提供重要的理论工具。

整理：邹晓龙、陈智强

Shun-ichi Amari是日本理化所的荣休教授，神经网络研究的教父级人物，一生做出了大量开拓性的成果，包括独立发展了信息几何（Information Geometry），首次提出了随机梯度下降算法（1967）、连续吸引子神经网络（1977）、Amari-Hopfield模型、nature gradient等。

01

 反向传播算法的历史

图1. 随机梯度下降算法

深度神经网络成功离不开反向传播算法，亦称随机梯度下降算法。随机梯度下降算法,假设x是输入，y是神经网络的输出。那么如何学习神经网络的参数W，我们可以基于训练数据D，构建一个损失函数，通过损失函数对参数W求梯度，即可以得到参数的更新值，如图1所示。 

图2. 随机梯度下降算法的历史

随机梯度算法在历史上曾多次被不同的研究者独立地提出。甘利先生是随机梯度算法的最早提出者之一。Rosenblatt在1958年提出了感知机模型，当时的感知机模型采用的是MCP神经元模型，即状态值为离散的0或者1，模型基于简单的感知机学习法则进行学习。

在上世纪60年代，甘利先生在研究这个问题时，为了克服多层感知机学习难题，考虑用一种非线性的模拟神经元来替代不可导的MCP神经元，并构建了一个可微分的，简单的平方损失函数，这样整个网络就变得可微分。其发展了一个新的学习算法来优化多层感知机，称之为随机梯度方法。类似的方法被很多人独立地提出，如Tsypkin（1966），Werbos（1974）等。但是囿于时代局限，甘利先生当时未能在计算机上进行模拟验证，而是重点对一些学习动力学行为进行了理论分析。Rumelhart和Hinton等人在1986年做出了类似的工作，并将其命名为反向传播算法。Rumelhart等人通过大量的计算机模拟实验，做出了很多令人兴奋的发现。至此，随机梯度算法用于优化多层神经网络逐步流行开来。

 

图3. 甘利先生在1960s采用的多层感知机模型，神经元采用的是模拟神经元，是深度网络最早用随机梯度下降算法进行学习仿真实例。

02

统计神经动力学研究历史

图4. 随机连接网络的统计神经动力学研究历史

统计动力学方法采用对随机变量进行统计平均的方式，对一些宏观的物理状态进行研究，如温度、熵等，这些宏观状态取决于粒子的微观物理规律。而统计神经动力学也采用类似方法，主要对随机连接的人工神经网络的一些宏观的行为进行推断，这些宏观行为由神经元的相互作用产生。在随机连接的神经网络中，其权值独立地从一个零均值的高斯分布采样得到。统计神经动力学想法最早源于Rozonoer （1969）和甘利先生 （1969，1971）的工作。甘利先生随后在1974和1977年进一步对统计神经动力学的数学理论进行了深入研究。近年来，甘利先生（2013），Poole（2016），S. Schoenholz（2017）等人将统计神经动力学方法应用于深度随机网络的研究，推进了我们对深度学习理论的理解。

图5. 统计神经动力学

如图5右上小图所示，一个简单的随机连接权值网络，输入为X，输出为Z。连接矩阵W为随机生成。此时网络表征了一个映射函数，从输入空间将X映射到输出空间中的Z。对于每一个随机网络，可以表示为参数空间中的一个点，如左上图所示，不同的点代表参数不一样的随机连接权值网络。不同的随机连接权值网络表征不同的映射函数，其行为各不一样。但是在一些统计的宏观状态上，不同的随机网络却是相似的。最简单的宏观统计状态为输入分布的均值, 输出分布的均值。通过研究这些宏观状态之间的统计规律，可以帮助我们更好的理解网络的动力学行为。

图6. 互馈随机网络可以产生振荡，联想记忆和混沌动力学现象

甘利先生很早就开始对互馈随机网络的统计神经动力学进行研究，在1968年发现了互馈随机网络可以产生神经振荡现象，这为大脑中的神经振荡现象提供了很好的理论模型（类似的研究在1971年被Wilson-Cowan提出）。在1972年，甘利先生进一步提出了联想式记忆模型，这为我们探讨大脑的记忆机制提供了很好的理论模型（类似的工作由Hopfield 1982年提出）。随后，在1988年，Sompolinsky等人采用统计神经动力学方法研究发现，互馈随机网络还可以产生混动动力学现象。

03

用统计神经动力学方法理解深度学习

图7. 深度随机网络的统计神经动力学

近年来，深度学习技术在不同的应用中取得了巨大的成功。深度神经网络的参数量远远多于训练样本数量，按照传统的机器学习理论，深度网络由于参数量巨大，会过拟合有限的训练样本，从而导致不好的泛化。但是实践中，深度网络却在测试数据集表现良好。目前，我们对于深度网络的理论理解严重滞后于应用实践，而统计神经动力学方法为我们理解深度学习提供了重要的理论工具。近年来，研究者们基于统计神经动力学方法对深度随机网络进行了大量研究，产生了很多优秀的理论工作。

图8. 平滑的输入曲线会随着深度随机网络一层层的非线性变换变得越来越复杂

Poole等人在2016年采用统计神经动力学方法研究在深度随机神经网络中，输入信号是如何在深度随机网络中一层层被转换并传播的：随着网络层的加深，深度随机网络的表征会产生有序到混沌的相变过程。Poole等人还进一步证实，这种深度随机网络表征的映射函数并不能有效地被浅层网络表征。如图8所示，一个平滑的输入曲线会随着深度随机网络一层层的非线性变换，逐步由平滑变得越来越扭曲。

图9. 深度网络的局部最小值和全局最优

机器学习中的优化目标函数常常是非凸的，如图9右上图所示，有很多局部最小值。优化学习过程中，模型的参数通常会困在一个局部最小点，而不能到达全局最优点。传统的观点认为，对于过参化的深度网络，其对应的损失函数会存在很多局部最小点，导致优化失败。但是实践中，深度神经网络却取得巨大的成功。Kawaguchi等人应用统计神经动力学方法研究发现，当深度网络的参数量足够大时，损失函数对应的局部最优点都取得了相似的全局最优值。

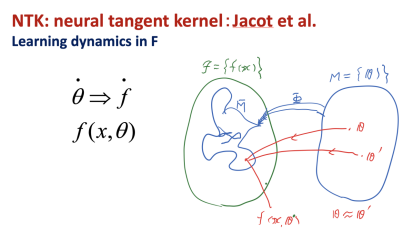
图10. 神经正切核理论

深度网络的参数空间可以被映射到一个泛函空间。我们也可以在这个泛函空间中研究深度学习的统计动力学行为。在2018年，Jacot等人发表了神经正切核的理论工作，其在泛函空间中对神经网络学习过程的统计神经动力学性质进行了研究。Jacot从理论上证明，当深度网络从一个随机初始化的权值出发进行训练学习时，我们总可以在初始化参数点局部的参数空间中，找到拟合目标函数的最优解，并且随机梯度学习过程在泛函空间中，可以被一个线性微分动力学方程描述。

图11. 在参数空间中，深度网络拟合目标函数的最优解存在于初始化参数点附近区域

Jacot这一有趣的结果如图11所示，深度神经网络不同的随机初始化参数集对应于参数空间中一个红色的点。当深度神经网络的参数量远远大于训练样本数量时，深度网络通过梯度学习，总可以在其局部参数空间区域找到一个拟合目标函数的点，局部区域为红点周围的蓝色区域。我们从中也可以看到，深度神经网络可以存在很多组参数解，其均可以拟合目标函数。

图12. 含有一个隐层的简单感知机模型

Jacot等人的工作用到了严格的数学分析，难以让人直观地理解理论背后的本质。甘利先生在最近的研究工作中给出了一个直观的几何解释：其首先考虑了一个最简化的模型，即只有一个隐层的感知机模型，如图12所示，并考虑输入到隐层之间的权值固定，梯度算法只需要学习隐层到输出之间的连接权值。

 

图13. 感知机模型拟合目标函数的通解，由最小范数解和零向量两部分组成

 

甘利先生首先从统计神经动力学的角度，证明当网络的隐层足够宽，而训练数据有限时，基于随机梯度下降法，深度网络的参数可以优化到达初始化参数附近的最小范数解。其位于n维的子空间Z中，n是训练样本的数量，并且和一个零子空间N正交。所以我们可以将网络的初始化参数的分布投影到子空间Z中，从而研究最小范数解的分布情况。

 

图14. 随机参数向量分布在一个半径为1的单位球体上

甘利先生给出了一个直观的几何解释。其指出网络的随机参数向量 可以视为分布在一个在半径为1的高维球体上，如图14所示。

 

 

图15. 高维球体分布在低维子空间的投影分布

由于网络的参数量远大于训练样本数量，当将高维的球体分布投影到一个低维的子空间时，会在低维的子空间形成一个零均值，协方差为的高斯分布。即当很大时，这个高斯分布形状会变得很尖，几乎所有的最小范数解都会集中在子空间Z原点的局部参数空间区域。甘利先生还进一步给出，对于一个一般性的大的深度随机网络，我们也总是可以在其很小的一个局部参数空间中，找到可以拟合任意目标函数的解，相关文章发表在2020年的neural computation期刊上。

04

信息几何、自然梯度下降和fisher信息矩阵

图16. 信息几何方法

信息几何方法主要是研究概率分布函数形成的流形，并揭示流形背后不变的几何结构和性质。甘利先生在40多岁时，提出了信息几何方法，并将其运用于人工神经网络的研究。如图16所示，深度网络的参数空间其实就对应着一个黎曼流形，我们可以用fisher信息矩阵作为黎曼测度，研究人工神经网络在黎曼流形上的统计神经动力学性质。

 

图17. 自然梯度下降方法

在1998年，甘利先生基于信息几何方法提出了经典的自然梯度下降法。随机梯度法是在参数空间中考虑优化问题，网络参数更新是沿着损失函数最陡峭变化方向进行，可以通过求解损失函数在参数空间的梯度得到。而自然梯度下降法是在黎曼流形空间上考虑优化问题。自然梯度下降法可以表示。其中是fisher信息矩阵的逆。fisher 信息矩阵包含了流形空间的几何结构信息，其收敛速度远超随机梯度下降算法。

 

 

图18. 对fisher信息矩阵进行近似

但是对于深度神经网络，fisher信息矩阵的逆，实际计算非常困难。近年来，很多近似计算fisher信息矩阵的方法被提出，如Ollivier 2015， Grosse&Martens 2016等。在甘利先生2019年的工作中，其用统计神经动力学的方法对一个深度随机网络的fisher信息矩阵进行了研究，发现大的深度随机网络的fisher信息矩阵存在特殊的结构，其可以被一个对角化矩阵近似，而近似后的fisher信息矩阵可以基于反向传播误差较为容易地计算得到。

最后，甘利先生提出的信息几何等统计神经动力学方法为我们提供了有力的数学工具，帮助揭示深度神经网络强大的表征、泛化等能力背后的数学理论基础。

---