基于深度学习（DL）的医学图像分割方法虽有显著进步，但实际场景中测试数据（目标域）与训练数据（源域）常存在，源于设备、患者人群、图像质量等差异，会严重降低模型在目标域的性能。

概率：模型对结果的“倾向性”；不确定性：模型对自身判断的“怀疑程度”；置信度：综合两者后对“预测可靠性”的最终评价。

org.xml.sax.SAXParseException; lineNumber: 27; columnNumber: 38;元素类型 "collection" 必须后跟属性规范 ">" 或 "/>"

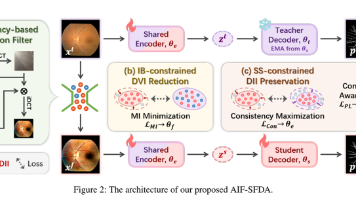
本文提出一种基于多图匹配的测试时领域泛化框架（TTDG），用于解决医学图像分割中的领域偏移问题。该方法通过构建图结构并引入宇宙嵌入实现多图匹配，利用形态学先验知识提升模型泛化能力。在视网膜和息肉分割数据集上的实验表明，该方法在多源和单源领域泛化任务中均优于现有方法，平均DSC最高提升19.09%。关键创新在于将循环一致性约束融入图匹配过程，有效捕获全局结构信息，并在测试时无需目标域标签即可快速适应

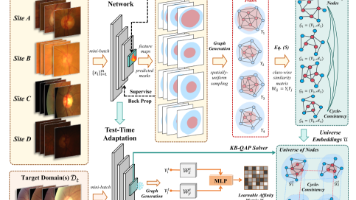
本文提出了一种基于SAM（Segment Anything Model）的IPLC框架，用于解决医学图像分割中的无源域适应（SFDA）问题。针对现有SFDA方法存在监督不足和伪标签噪声的挑战，IPLC框架通过多次随机采样和熵权重估计生成鲁棒伪标签，结合平均负曲率最小化实现平滑分割，并采用迭代修正学习策略逐步优化模型。在M&MS心脏MRI数据集上的实验表明，该方法在四个不同扫描仪域上均显著优

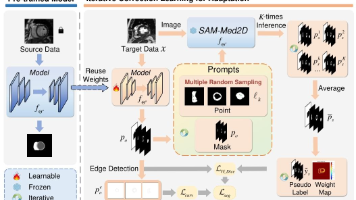
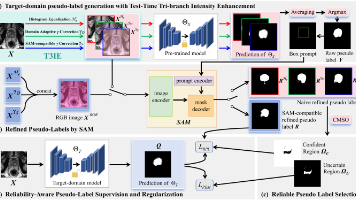
本文提出SRPL-SFDA方法，解决医学图像分割中的无源源域自适应问题。通过测试时三分支强度增强(T3IE)生成兼容SAM的伪标签，利用多SAM输出一致性(CMSO)筛选可靠区域，并设计可靠性感知训练损失(RPSR)区分监督。在前列腺和胎儿脑MRI数据集上，Dice系数分别提升4.95%和1.69%，接近全监督性能。创新性地利用SAM的零样本能力优化伪标签，无需微调或源域数据，具有模型无关性。未来

输入样例212输出样例27二维平面问题大部分都可以套用公式y(平面数）=ax2+bx+c(x为直线个数）带入三个点求出a,b,c得到公式~此题我带入的x是2，3，4 ：4a+2b+c=7;9a+3b+c=16;16a+4b+c=29；求出a=2,b=-1;c=1;即公式y=2x2-x+1.#include<iostream>#include<algorithm>using