bootloader写成后，需要处理传送过来的.Hex，或者等价的文件的烧录。MicroChip官方并未给出一个.Hex转为.Bin的处理策略。在它的Bootloader代码中，我们可以大致看到它的实现机制，它定义了一组命令。上位机在处理升级时，与Bootloader要通过这组指令进行信息传递。这是一个交互式的协议。如果我们抛开这个交互协议，希望自己处理升级过程，那么，需要对.Hex文件本身进行处

GeForce RTXTM 3070 Ti 和 RTX 3070 显卡采用第 2 代 NVIDIA RTX 架构 - NVIDIA Ampere 架构。该系列产品搭载专用的第 2 代 RT Core ，第 3 代 Tensor Core、全新的 SM 多单元流处理器以及高速显存，助您在高性能要求的游戏中所向披靡。3090量化到FP32，使用官方的Pytorch跑，完整的60 classes coc

温振分析过程中涉及到的一些知识点，期望能尽可能铺满与工程应用相关的领域，指出那些可能的陷阱。

GeForce RTXTM 3070 Ti 和 RTX 3070 显卡采用第 2 代 NVIDIA RTX 架构 - NVIDIA Ampere 架构。该系列产品搭载专用的第 2 代 RT Core ，第 3 代 Tensor Core、全新的 SM 多单元流处理器以及高速显存，助您在高性能要求的游戏中所向披靡。3090量化到FP32，使用官方的Pytorch跑，完整的60 classes coc

不知道大家是否意识到这个问题，在进行yolo训练时，因为从ultralytics拿到的预训练模型中已经包含了80类物体的识别参数。现在比如说，我们要识别一个新物体，比如：月饼，此时，我们该怎么做?我能想到的最佳实践，还是先对新增的数据集进行预标注，然后对新增物体的标注，混合进预标注文件里，然后，再进行训练。因为新增识别对象会增大模型的参数（虽然只是线性的增加，但是仍然会有不良后果），所以，建议在y

现代嵌入式芯片的的一些名词解释和图例。包括BGA，QFP这类典型封装，DIP这类已经不太常用的封装未提及。

在谐振电感和电容的充放电过程中，励磁电感因为阻抗太大，他的电流变化的幅度无法跟上谐振频率，所以，在谐振分析中，更多地表现为一种类似直流偏置的器件存在。也正是因为这种偏置作用，它在实际消耗有功功率。一般说来，励磁电感Lm远大于谐振电感Lr，在发生谐振时，在这个频点，励磁电感其实对能量转换其实来不及响应。谐振的震荡主要在Lr,Cr之间震荡。一般说来,LLC电路中的主变压器Lm励磁电感不参与谐振频率计算

在一本振动分析书籍中提到的方根幅值，初看似乎不如方均根（RMS）实用，因为RMS通过先平均再开方的方式，通常误差更小。然而，深入分析后发现，对于归一化在[0,1]范围内的测量值，方根幅值实际上能更有效地减小误差。特别是当数值小于1时，方根幅值通过sqrt()函数处理后，误差会缩小。尽管在累加过程中误差可能被放大，但累加后的平均化处理使得整体误差得到控制。因此，对于小信号处理，方根幅值在均值计算中展

这篇文章探讨了字符串替换函数gp_str_replace的潜在缺陷，并展示了AI在代码分析中的局限性。作者通过具体案例演示了：AI在分析代码时容易陷入逻辑误区，一些僵化的思维方式，可能会在某些问题回答过程中陷入死循环，这种AI的分析盲区可能具有普遍性，类似弱点在实战中可能被利用。在觉察到AI的僵化处理策略，让其提交具体案例反证，而非直接提问，可以更有效地测试AI的代码分析能力。

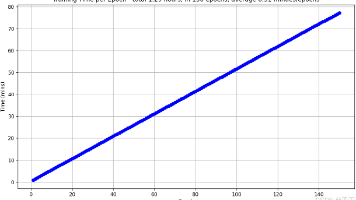
两次训练的数据集，nvidia3090上跑的还要多10%的数据。nvidia环境没有做优化。nvidia3090的训练速度是i7-13700 2.4G的20倍。