深度学习本身是一个非常庞大的方向， 其下属的研究内容十分广泛，且颇具研究价值。而本文的内容，是一篇导论性质的文章，仅供初入机器学习和深度学习的学者们参考。随着人工智能的兴起和计算机算力的不断提升，深度学习从机器学习的众多方向中脱颖而出，并不断迸发出强烈生机。基于此，近年来有关深度学习的研究在不断更新，不断前进，有关它的相关领域也早已形成了自己特有的一些研究范畴。

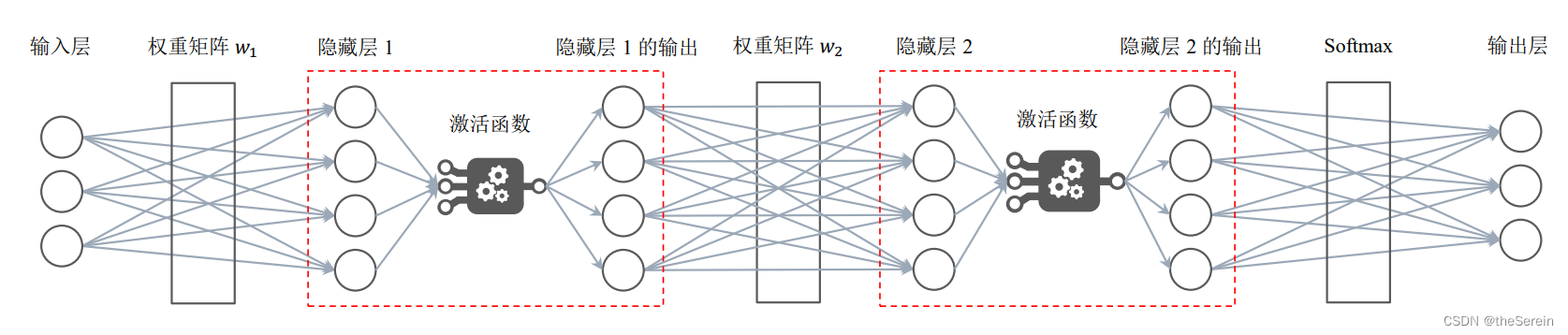
导入手写数字数据集Mnist失败的解决办法：ImportError: cannot import name 'fetch_mldata' from 'sklearn.datasets' (D:\Python\Python3.9\lib\site-packages\sklearn\datasets\__init__.py)

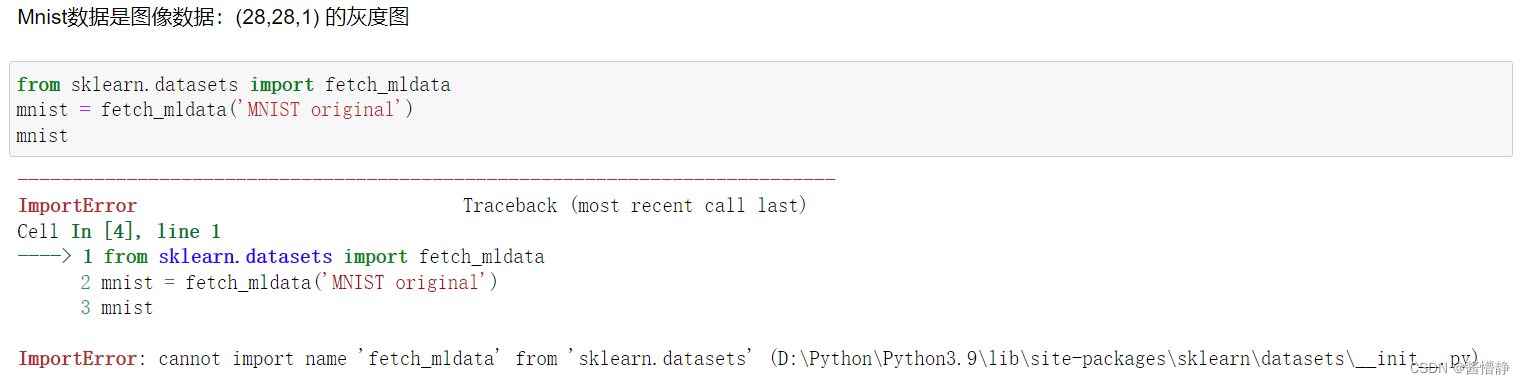
决策边界的绘制步骤如下:① 构建坐标数据，合理的范围当中，根据实际训练时输入数据来决定（可参考 iris.DESCR）② 整合坐标点，得到所有测试输入数据坐标点③ 预测，得到所有点的概率值④ 绘制等高线，完成决策边界

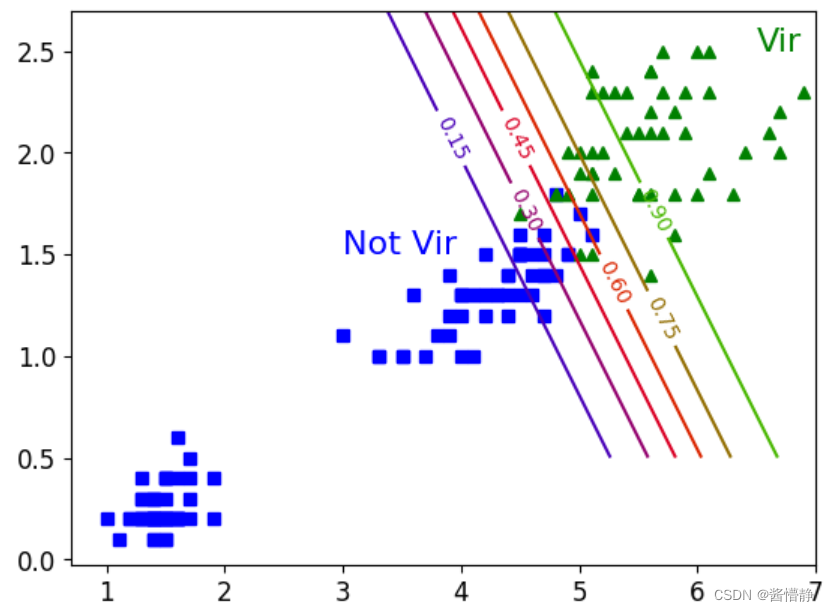
首先计算在所有数据上的损失值，然后再进行梯度下降。具体操作步骤是：遍历全部数据集算一次损失函数，然后算函数对各个参数的梯度，并更新梯度。这种方法每更新一次参数，都要把数据集里的所有样本计算一遍，因此得出的梯度往往都是朝着正确的方向；但是其缺陷是计算量过大，导致计算速度慢，因而不支持在线学习。

EM算法的思路如下：1. 给 𝜃~𝐴~ 、 𝜃~𝐵~ 一个初始值；2. 分别计算每组实验在抛掷硬币A、硬币B的情况下所得概率，并根据该概率值去分别计算两硬币正面朝上次数的期望值。因此，此步骤也被称为“E过程”；3. 分别用第 2 步中计算的每组期望值来计算 𝜃~A~^(𝑖)^、𝜃~B~^(𝑖)^；4. 将计算得到的 𝜃~A~^(𝑖)^、𝜃~B~^(𝑖)^ 回代第 2、3 步

首先计算在所有数据上的损失值，然后再进行梯度下降。具体操作步骤是：遍历全部数据集算一次损失函数，然后算函数对各个参数的梯度，并更新梯度。这种方法每更新一次参数，都要把数据集里的所有样本计算一遍，因此得出的梯度往往都是朝着正确的方向；但是其缺陷是计算量过大，导致计算速度慢，因而不支持在线学习。

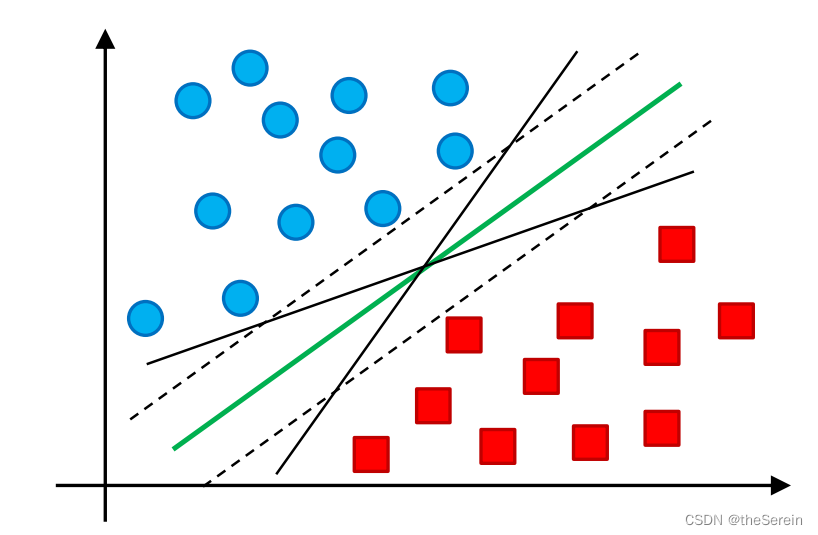
支持向量机（Support Vector Machine, SVM）是一类按监督学习方式对数据进行二元分类的广义线性分类器，其决策边界是对学习样本求解的最大边距超平面。支持向量机作为传统机器学习算法中的霸主，其背后的数学知识是相当复杂且精密的。

EM算法的思路如下：1. 给 𝜃~𝐴~ 、 𝜃~𝐵~ 一个初始值；2. 分别计算每组实验在抛掷硬币A、硬币B的情况下所得概率，并根据该概率值去分别计算两硬币正面朝上次数的期望值。因此，此步骤也被称为“E过程”；3. 分别用第 2 步中计算的每组期望值来计算 𝜃~A~^(𝑖)^、𝜃~B~^(𝑖)^；4. 将计算得到的 𝜃~A~^(𝑖)^、𝜃~B~^(𝑖)^ 回代第 2、3 步

线性回归的目的，是根据已知的特征信息 X 和对应的函数值 y ，来寻找一个能尽可能拟合真实情况的回归方程（即求出 θ 向量）。在概率论中，若已知一组观测数据和这组数据服从的分布，我们要如何求出该组数据满足的分布的具体数值呢？一个比较直观的方法是：极大似然估法。

聚类分析，即聚类（Clustering），是指在一大推数据中采用某种方式或准则来将一些具有相同或相似性质和特征的数据划分为一类。聚类是无监督学习的典型算法，相较于有监督学习，由于聚类针对的大多是无标签数据，因此对于最终构建的模型而言，在进行模型评估时会比较麻烦。同时，在对算法进行调参时也会因为这种不确定性而稍带困难。