
简介
该用户还未填写简介
擅长的技术栈
可提供的服务
暂无可提供的服务
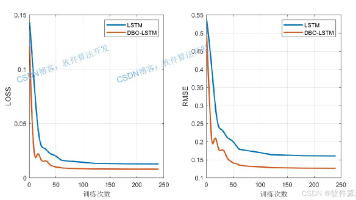
本文提出了一种基于蜣螂优化算法(DBO)改进的LSTM预测模型(DBO-LSTM)。该模型通过模拟蜣螂的滚球、跳舞和觅食三种行为,优化LSTM网络的隐含层数量和初始权重等关键参数,解决了传统LSTM依赖经验设置参数导致预测精度不足的问题。算法采用适应度函数评估预测误差,通过滚球行为实现全局搜索,跳舞行为进行局部开发,觅食行为保持多样性。实验结果表明,DBO-LSTM在MATLAB环境下具有较好的预
实际应用中,CS模型和CV模型可以结合使用,先通过CS模型进行初步聚类和目标候选,然后在每个簇内应用CV模型的投票机制进行目标确认和数据关联优化。基于CS模型和CV模型的多目标协同滤波跟踪算法matlab仿真,在计多目标跟踪领域,基于CS模型和CV模型的多目标协同滤波跟踪算法是近年来发展起来的先进技术,旨在提高在复杂场景下对多个移动目标的跟踪精度和鲁棒性。基于CS模型和CV模型的多目标协同滤波跟踪

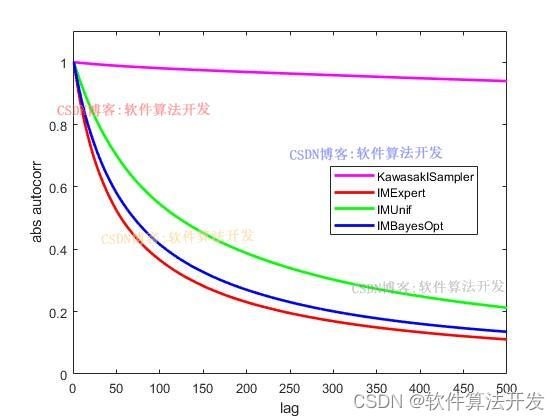
基于贝叶斯优化的自适应马尔科夫链蒙特卡洛(Adaptive Markov Chain Monte Carlo, Adaptive-MCMC)算法是一种结合了贝叶斯优化思想与MCMC抽样技术的高级采样方法,旨在高效地探索复杂的概率分布,特别是那些具有多模态、强相关性或非凸性的分布。核心在于建立一个代理模型(通常是高斯过程)来近似未知的目标函数,并使用采集函数(如期望改善(EI)、上限置信区间(UCB
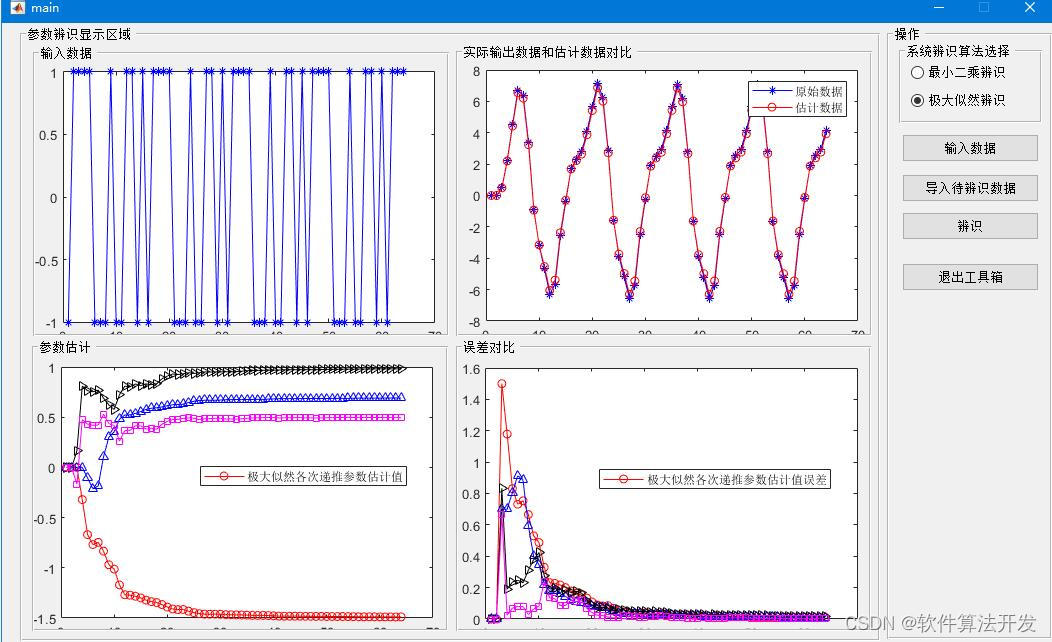
一般来说,这个模型只是对象的输入输出特性在某种准则意义下的一种近似,挖的程度取决于人们对系统先验知识的认识深化程度和对数据集合性质的了解,以及所选用的辨识方法是否合理。而最小二乘法基于误差平方和最小的原则,通过最小化观测数据与模型输出之间的误差平方和来估计系统参数。在系统参数辨识中,最小二乘法通常假设观测数据与模型输出之间存在线性关系,并通过最小化观测数据与模型输出之间的误差平方和来估计系统参数。
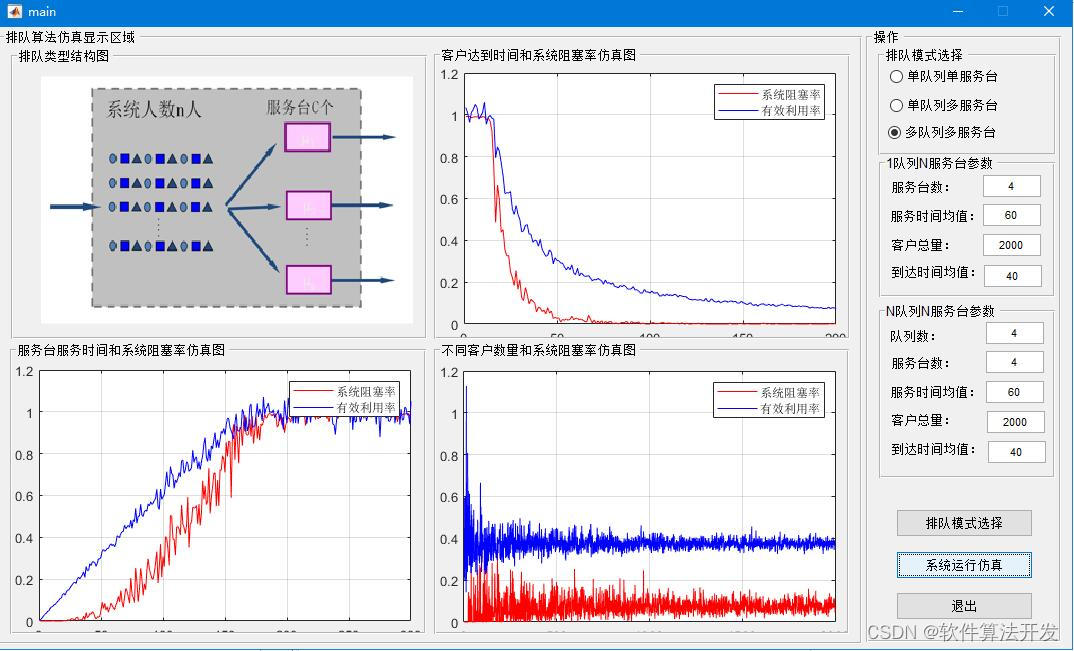
排队系统是基本的离散事件系统,了解掌握离散事件系统是研究排队系统仿真不可或缺的前提。排队论(Queueing Theory)是一门研究系统中顾客和服务台交互行为的学科,主要关注在有限资源约束下,顾客到达系统并等待服务的过程。在实际应用中,排队论的目标通常是确定各种性能指标(如等待时间、利用率、服务水平等),以便设计出合理的服务策略和资源分配方案,以最小化成本或最大化服务质量。排队算法的matlab
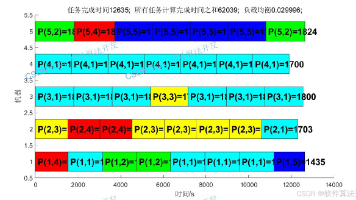
摘要:本文提出一种PSO-NSGAIII混合算法用于解决多目标生产调度问题。该算法融合粒子群优化(PSO)的快速收敛性和NSGAIII的多目标优化能力,通过非支配排序、参考点关联和粒子更新等7个核心步骤,在MATLAB环境下实现了对生产周期、成本、能耗等多目标的优化。实验结果表明,相较于单一算法,该混合算法能有效平衡解的收敛性和多样性,为复杂生产调度问题提供更优解决方案。
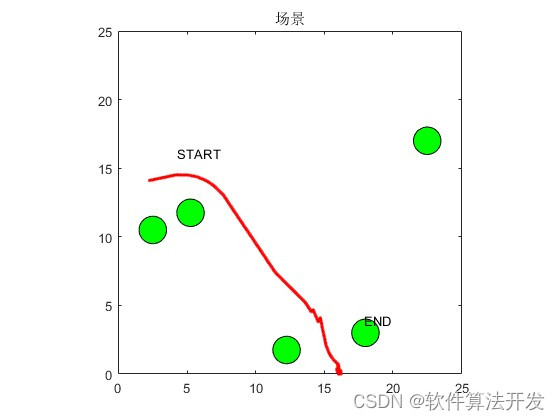
在移动机器人领域,路径规划是一个核心任务,目标是在未知或已知环境中为机器人寻找一条从起始点到目标点的安全、有效且满足特定约束条件(如避障、最短距离等)的路径。数学上,通常将环境表示为一个离散或者连续的空间,并通过图论中的搜索算法来解决。
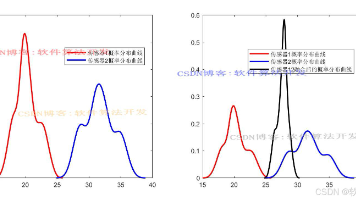
在多传感器数据融合的诸多方法中,贝叶斯估计凭借其坚实的理论基础和强大的处理不确定性信息的能力,占据着举足轻重的地位。在实际应用场景中,传感器所采集的数据往往不可避免地带有噪声、干扰以及不确定性,而贝叶斯估计恰能巧妙地处理这些问题,通过对先验知识和观测数据的综合考量,给出对目标状态的最优估计。这个先验分布可以基于历史数据、专家知识或系统的初始假设来确定。基于贝叶斯估计的多传感器数据融合算法matla
基于贝叶斯优化的自适应马尔科夫链蒙特卡洛(Adaptive Markov Chain Monte Carlo, Adaptive-MCMC)算法是一种结合了贝叶斯优化思想与MCMC抽样技术的高级采样方法,旨在高效地探索复杂的概率分布,特别是那些具有多模态、强相关性或非凸性的分布。核心在于建立一个代理模型(通常是高斯过程)来近似未知的目标函数,并使用采集函数(如期望改善(EI)、上限置信区间(UCB

例如,在弹性模量与密度的关系中,使用幂律插值公式 E(ρ)=E0ρp (其中 E0 是实体材料的弹性模量,ρ是单元密度,p是惩罚因子),这种关系简单直接,易于理解和实现。材料结构的拓扑优化旨在通过材料分布的优化设计,在满足约束条件下实现特定性能目标(如最小柔顺度、最大刚度等)。有限元方法是一种成熟的结构力学分析工具,SIMP算法可以直接利用有限元软件的计算结果,避免了重新开发复杂的力学分析模块











