第11章 时间序列时间序列数据在很多领域都是重要的结构化数据形式，例如金融、经济、生态学、神经科学和物理学。在多个时间点观测或测量的数据形成了时间序列。许多时间序列是固定频率的，也就是说数据是根据相同的规则定期出现的，例如每15秒、每5分钟或每月1次。时间序列也可以是不规则的，没有固定的时间单位或单位间的偏移量。最简单和最广泛使用的时间序列是那些由时间戳索引的。11.1 日期和时间数据的类型及工具

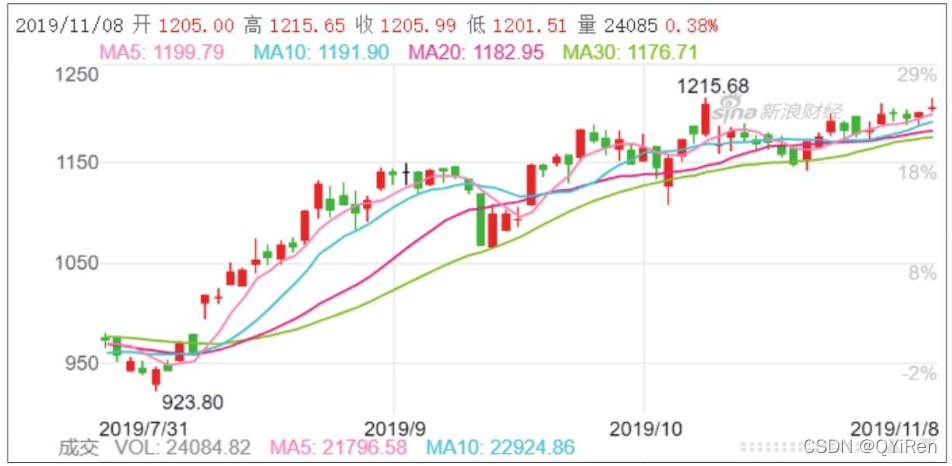
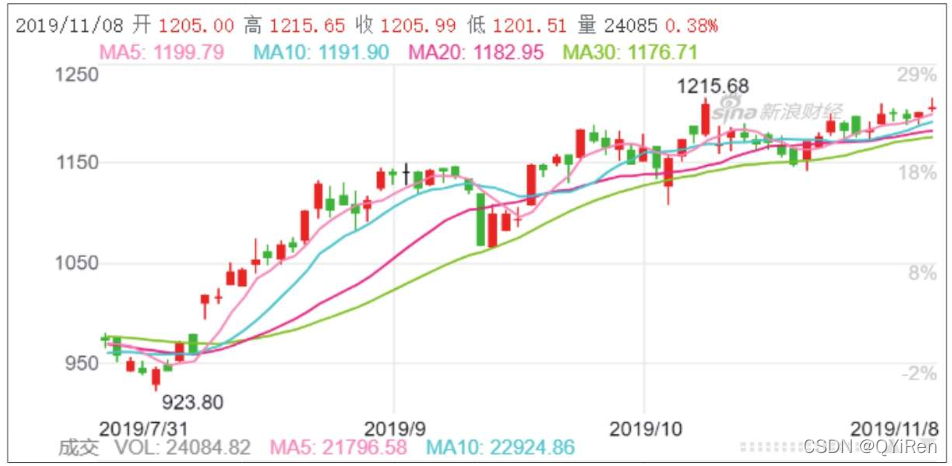
目录1 股票K线图知识了解2用Python绘制股票K线图2.1安装绘制K线图的mpl_finance库2.2引入相关库2.3用Tushare库获取股票基本数据2.4日期格式调整及表格转换2.5绘制K线图2.6添加均线图2.7添加每日成交量柱形图1 股票K线图知识了解下图所示为“贵州茅台”股票的日线级别的K线图：K线图中的柱形通常称为“K线”，因为形似蜡烛，所以也称为蜡烛图。K线是根据股票的4个价格

Python数据分析小案例

注：参考书籍《Python数据结构与算法》1.图的抽象数据类型定义Graph()新建一个空图；addVertex(vert)向图中添加一个顶点(vert)实例;addEdge(fromVert,toVert)向图中添加一条有向边，用于连接顶点fromVert，toVertaddEdge(fromVert,toVert,weight)向图中添加一条带权重(weight)的有向边getVertex(v

#用Python实现多元线性回归#当结果值得影响因素有多个时，可以采用多元线性回归模型。#例如，商品的销售额可能与电视广告投入、收音机广告投入、报纸广告投入有关系#使用pandas读取数据import pandas as pddata = pd.read_csv('Advertising.csv')# print(data.head())#显示前五行数据# print(data.tail())#显

在实际工作中获取到的数据往往不那么理想，可能会存在非数值类型的文本数据、重复值、缺失值、异常值及数据分布不均衡等问题，因此，在进行数学建模前还需要对这些问题进行处理，这项工作称为特征工程。特征工程通常分为特征使用方案、特征获取方案、特征处理、特征监控几大部分，其中特征处理是特征工程的核心内容，有时称为数据预处理。...

第11章 时间序列时间序列数据在很多领域都是重要的结构化数据形式，例如金融、经济、生态学、神经科学和物理学。在多个时间点观测或测量的数据形成了时间序列。许多时间序列是固定频率的，也就是说数据是根据相同的规则定期出现的，例如每15秒、每5分钟或每月1次。时间序列也可以是不规则的，没有固定的时间单位或单位间的偏移量。最简单和最广泛使用的时间序列是那些由时间戳索引的。11.1 日期和时间数据的类型及工具

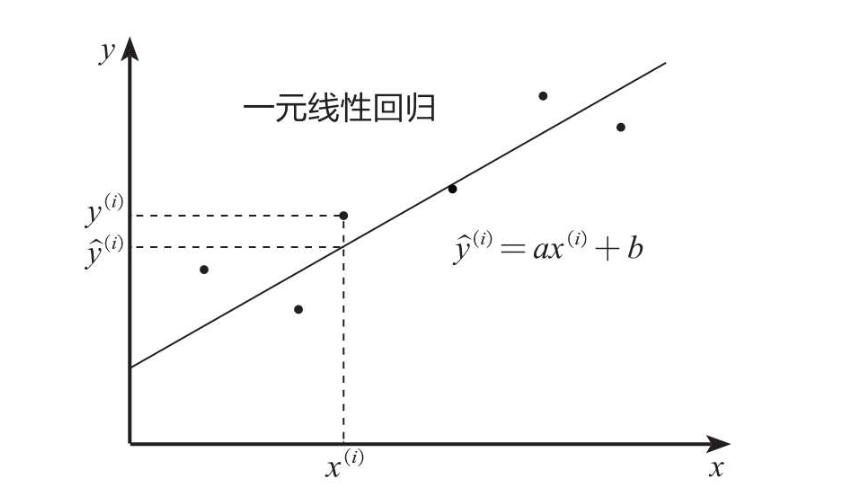
目录1 一元线性回归简介2 一元线性回归数学形式3案例：不同行业工龄与薪水的线性回归模型3.1案例背景3.2具体代码3.3模型优化4总体展示5线性回归模型评估6模型评估的数学原理6.1 R-squared6.2Adj.R-squared6.3 P值参考书籍1 一元线性回归简介线性回归模型是利用线性拟合的方式探寻数据背后的规律。如下图所示，先通过搭建线性回归模型寻找这些散点（也称样本点）背后的趋势线

Python数据分析小案例

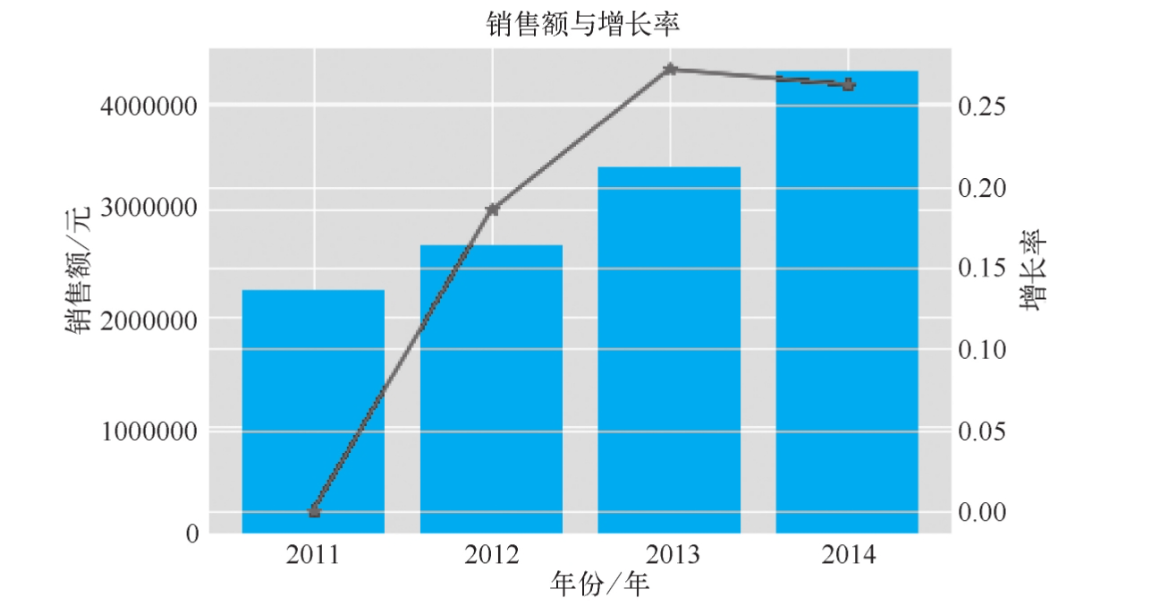
目录1.背景2.分析目标3.数据准备4.数据清洗4.1查看是否含有缺失值4.2查看是否有异常值4.3数据整理5.具体目标分析5.1分析每年销售额的增长率5.2各个地区分店的销售额5.3销售淡旺季分析5.4新老客户数5.5用户价值度RFM模型分析6.案例结论6.1结论依据6.2案例结论1.背景随着电商的不断发展，网上购物变得越来越流行。更多电商平台崛起，对于电商卖家来说增加的不只是人们越来越高的需求