执行完上述操作后，在 yolov5 文件夹下打开终端，输入以下命令。多了 __pycache__ 、 runs 和 yolov5s.pt 三个文件。这些字节码文件使得后续运行相同脚本时，加载速度更快，因为 Python 不需要重新编译源代码。__pycache__ 文件夹：当 Python 脚本首次运行时，解释器会将。检测结果会保存在 /yolov5/runs/detect/exp/ 文件夹下。环

在实际的处理中，由于测量传感器只能测量离散化的值，在精度不高的应用场景中，我们通常会选择忽略后面三项，只保留最简单的转换关系。注意：能被各种传感器（车速传感器，轮速计）测量到的速度是车体系速度，进行线性化得到的雅可比矩阵，即运动方程对状态。进行线性化得到的雅可比矩阵，即观测方程对状态。，后续噪声的符号会变化，但表示的意义不变。其中 t 为平移向量。为观测方程在当前时刻预测状态。为运动方程在上一时刻

高精地图本质上是结构化的矢量数据。常见的高精地图标准包括 OpenDrive，LaneLet2，Apollo OpenDrive 等。计算机上的高精地图通常由一些专用的绘制软件生成（例如 Arcgis，Autoware map tool等)。L2 在技术实现上会更倾向于实时感知，乃至可以使用感知结果直接构建。（bird eye view, BEV），而 L4 则依赖。

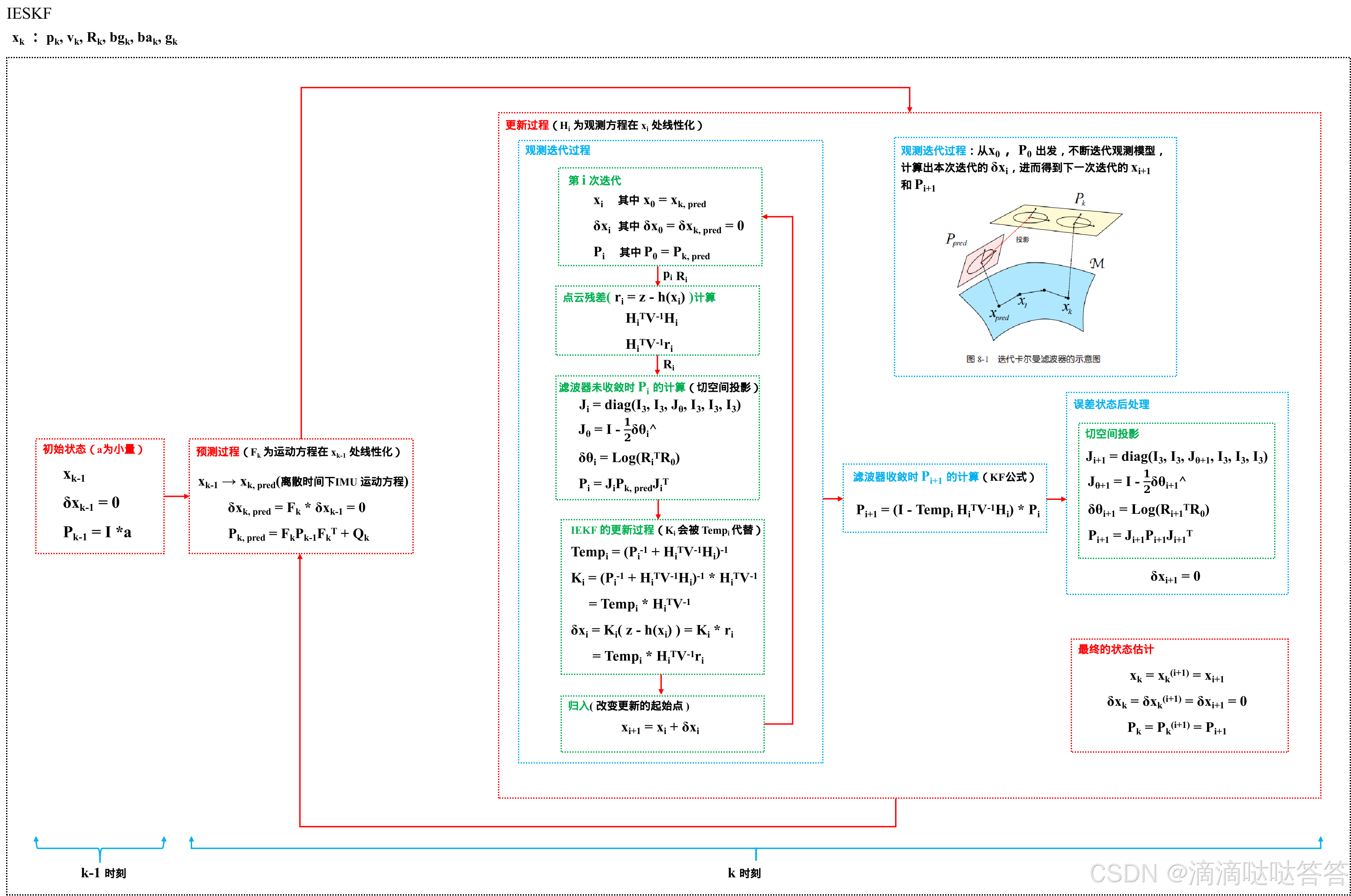
紧耦合系统，就是把点云的残差方程直接作为观测方程，写入观测模型中。这种做法相当于在滤波器或者优化算法内置了一个 ICP 或 NDT。因为 ICP 和 NDT 需要迭代来更新它们的最近邻，所以相应的滤波器也应该使用可以迭代的版本，ESKF 对应的可迭代版本的滤波器即为 IESKF。基于 IESKF 的紧耦合 LIO 系统的流程图如下所示：IESKF 的状态变量及运动过程 和 前文介绍过的 ESKF

增加卷积层的层数，构建更深的网络。添加池化层，降低分辨率，聚合信息。随着分辨率的降低，每个神经元所覆盖的区域也会增大，即感受野增大。

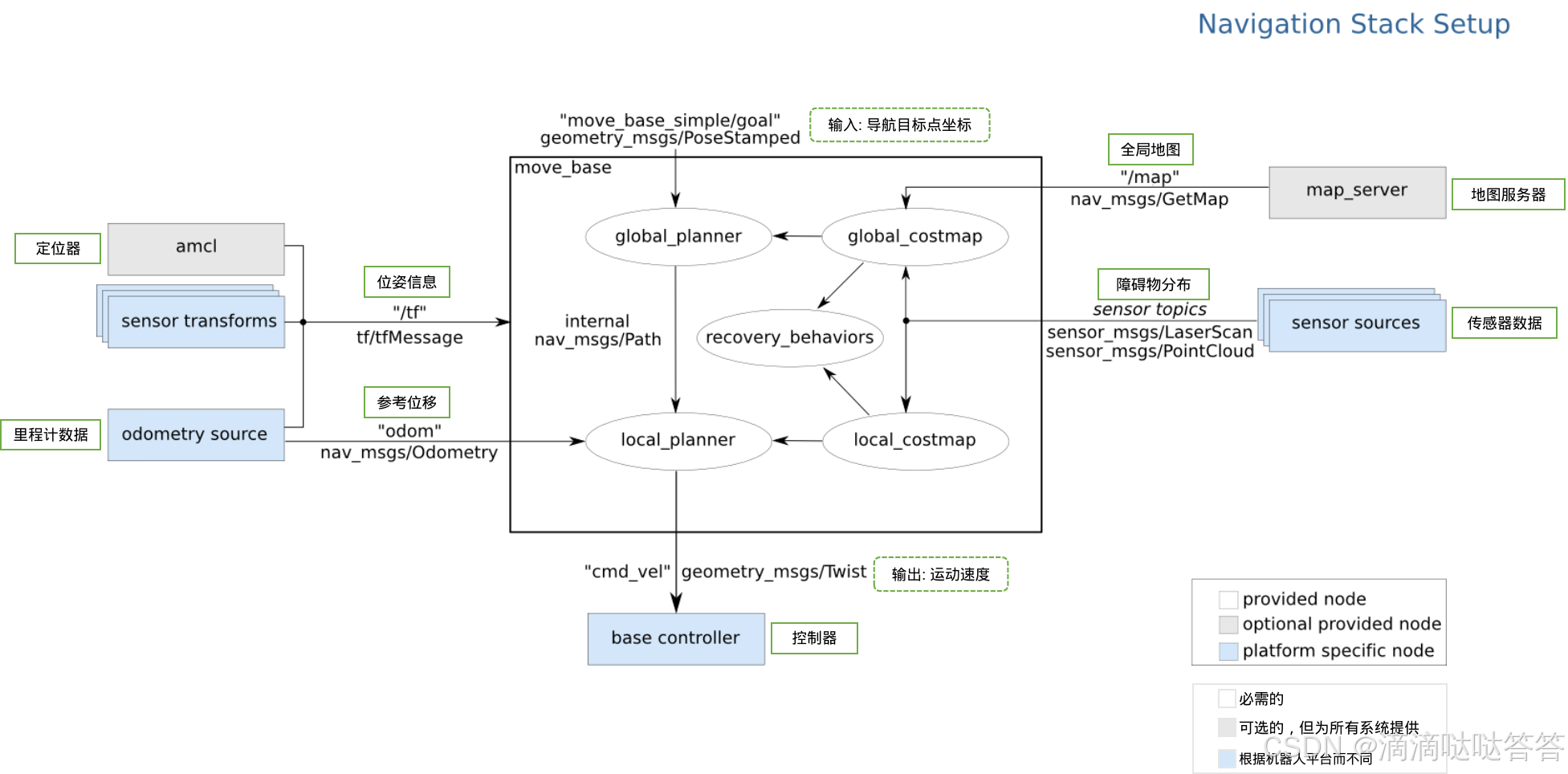
move_base支持自己编写自定义全局规划器，提供了一种 Plugin 插件接口，只要按照特定的格式，就能把自己的路径规划算法编写成新的规划器，加载到 move_base 节点中使用。

在 Ubuntu（或其他 Linux 系统）中，

这里使用《自动驾驶与机器人中的SLAM技术》ch4：预积分学中提到的散装的形式来实现预积分的顶点部分，所以每个状态被分为位姿（）、速度、陀螺零偏、加计零偏四种顶点（共 15 维）。后三者实际上都是的变量，可以直接使用继承来实现。g2o 部分可参考。1. 相比 ESKF，基于预积分的图优化方案可以累积 IMU 读数。累积多少时间，或者每次迭代优化取多少次，都可以人为选择。而 ESKF 默认只能迭代一

处理同步之后的点云和 IMU。初始化完毕后，先使用 IMU 数据进行预测，再用预测数据对点云去畸变，最后对去畸变的点云做配准。前文已经得到了去畸变的点云，这里只需将其传递给增量 NDT 里程计，并使用滤波器预测得到的先验位姿作为增量 NDT 里程计的初始位姿，经过迭代计算后得到优化后的位姿后再返回给滤波器，滤波器进行观测过程。），其存储上一 IMU 时刻 ESKF 的名义状态变量和当前 Measu

和组合导航一样，也可以通过加上来实现。一些现代的 Lidar SLAM 系统也采用了这种方式。相比滤波器方法来说，预积分因子可以更方便地整合到现有的优化框架中，从开发到实现都更为便捷。