中序线索二叉树在 n 个结点的二叉链表中，有（n+1）个空指针域，利用这些空指针域来存放当前结点的直接前驱和后继的线索，可以加快查找速度。普通二叉树只能找到结点的左右孩子信息，而结点的直接前驱和直接后继只能在遍历中获得，若将遍历后对应的前驱和后继预存起来，从第一个结点开始就可以顺藤摸瓜而遍历整棵树，树实际变成了线性序列。例如中序遍历的结果实际上就是把二叉树转化成了线性排列。线索二叉树的结构声明ty

二叉树的最大宽度求二叉树的宽度，我们首先想到他是广度（宽度）优先遍历的专利，记录每层结点数，取最大返回就是二叉树的宽度，如果我们想要用非递归的办法来解决的话，就需要设置一个数组来存储每层的结点数，然后引用一个 max 来记录最大结点数。这样的话就是相当于把非递归强行写成了递归，递归只起到了遍历的作用，所以此时更新 max 的时机可以是前中后任何一个地方。代码如下：#include<iostr

树的孩子兄弟表示法也叫树的二叉树表示法。树的左指针指向自己的第一个孩子，右指针指向与自己相邻的兄弟。结构的最大优点是：它和二叉树的二叉链表表示完全一样。可利用二叉树的算法来实现对树的操作 。左孩子右兄弟表示的树的高度因为二叉树表示法的根节点没有右孩子，所以树高就是左子树树高 + 1。然后我们看下根节点第一个孩子的高度，由于第一个孩子的右子树和第一个孩子的高度是相同的，所以比较左子树 + 1的高度来

并查集并查集用来判断一个图中的两个点是否连通，通过标记确定该成员所在的团队，每个团队都有自己的领头羊。我们给每个成员赋初值为 -1 ，那么下标对应值为 -1 的即为这个团队的领头羊。vector<int> parent(6,-1);每个团队都有自己的代理人，如何找到它呢？顺着这个成员往它的上级找，找到标记为 -1 的成员，就抓住了领头羊。//查询操作int getFather(int

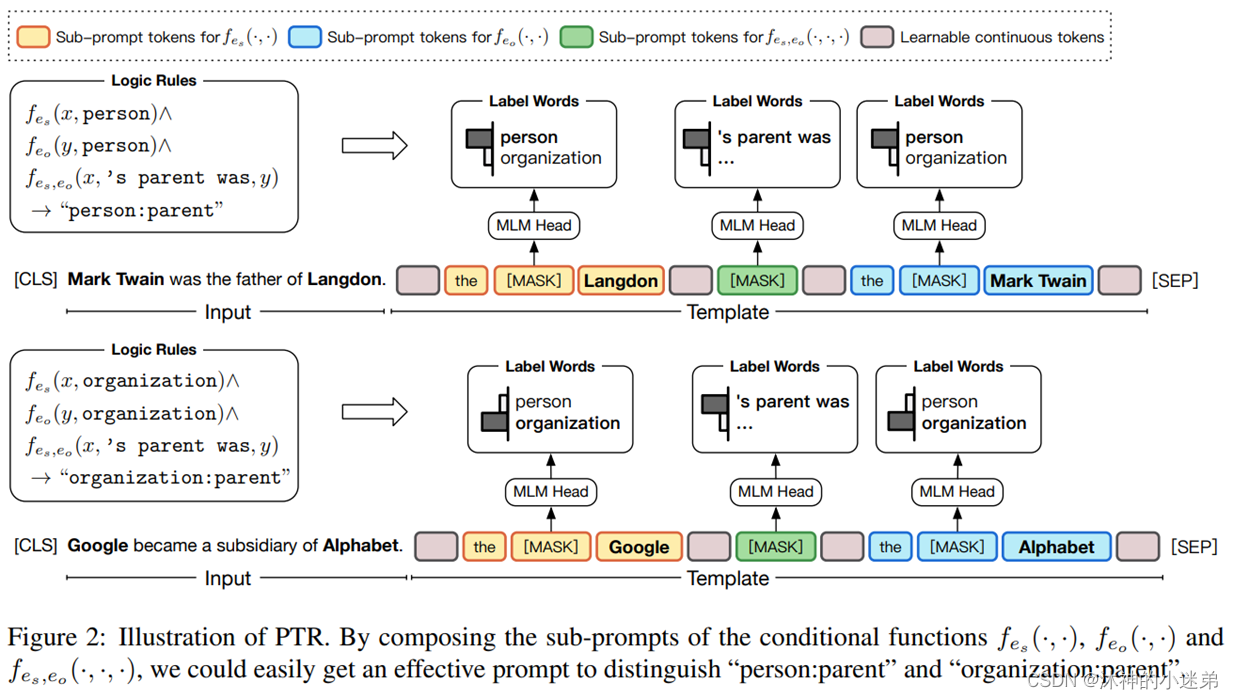
PTR-prompt关系抽取-2021