不同序列长度的多对多序列预测
回答问题
我的问题是使用 Keras 的 LSTM 层在给定先前时间步(t_{-n_pre}, t_{-n_pre+1} ... t_{-1})的情况下预测一系列值(t_0, t_1, ... t_{n_post-1})。
Keras 很好地支持了以下两种情况:
-
n_post == 1(多对一预测) -
n_post == n_pre(多对多预测,序列长度相等)
但不是n_post < n_pre所在的版本。
为了说明我需要什么,我使用正弦波构建了一个简单的玩具示例。
多对一模型预测
使用以下模型:
model = Sequential()
model.add(LSTM(input_dim=1, output_dim=hidden_neurons, return_sequences=False))
model.add(Dense(1))
model.add(Activation('linear'))
model.compile(loss='mean_squared_error', optimizer='rmsprop')
预测看起来像这样: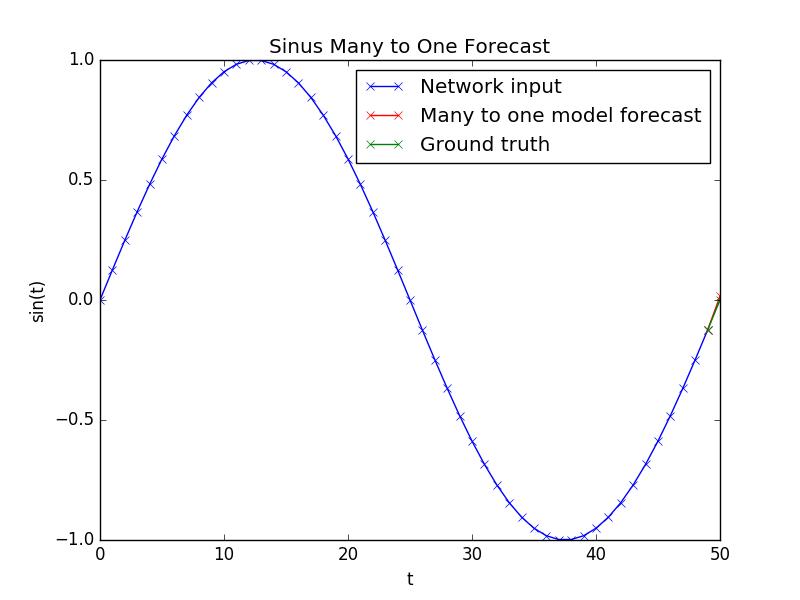
使用 n_pre u003du003d n_post 进行多对多模型预测
网络学习用这样的模型很好地拟合具有 n_pre u003du003d n_post 的正弦波:
model = Sequential()
model.add(LSTM(input_dim=1, output_dim=hidden_neurons, return_sequences=True))
model.add(TimeDistributed(Dense(1)))
model.add(Activation('linear'))
model.compile(loss='mean_squared_error', optimizer='rmsprop')
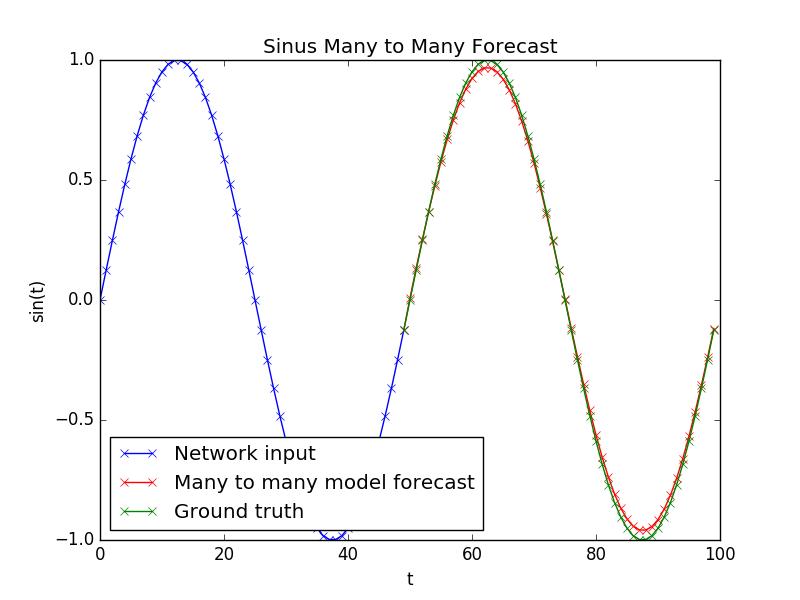
n_post < n_pre 的多对多模型预测
但是现在,假设我的数据如下所示:dataX 或输入:(nb_samples, nb_timesteps, nb_features) -> (1000, 50, 1)dataY 或输出:(nb_samples, nb_timesteps, nb_features) -> (1000, 10, 1)
经过一番研究,我找到了一种在 Keras 中处理这些输入大小的方法,使用如下模型:
model = Sequential()
model.add(LSTM(input_dim=1, output_dim=hidden_neurons, return_sequences=False))
model.add(RepeatVector(10))
model.add(TimeDistributed(Dense(1)))
model.add(Activation('linear'))
model.compile(loss='mean_squared_error', optimizer='rmsprop')
但是预测真的很糟糕: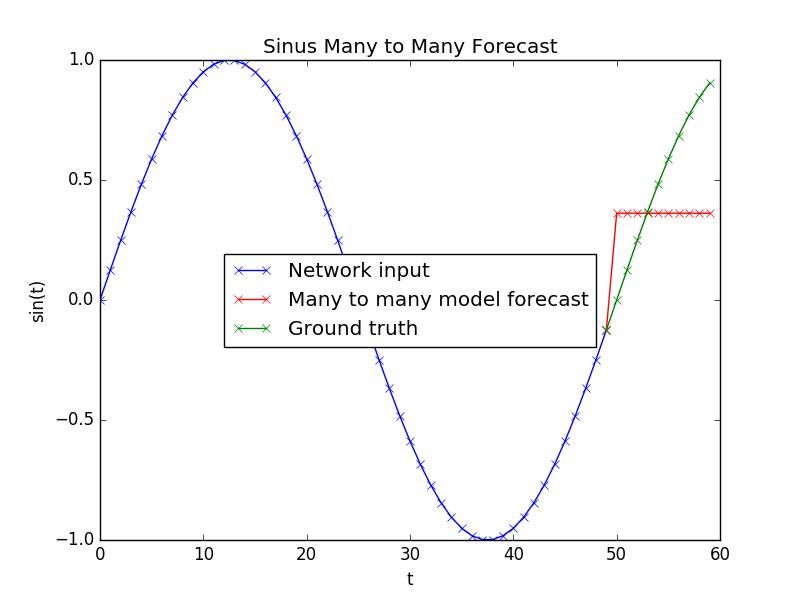
现在我的问题是:
-
如何使用
n_post < n_pre构建一个不会丢失信息的模型,因为它有一个return_sequences=False? -
使用
n_post == n_pre然后裁剪输出(训练后)对我来说不起作用,因为它仍然会尝试适应很多时间步长,而只有前几个可以用神经网络预测(其他的没有很好的相关性和会扭曲结果)
Answers
在 Keras Github 页面上提出这个问题后,我得到了答案,为了完整起见,我将其发布在这里。
解决方案是在使用RepeatVector将输出整形为所需的输出步数后,使用第二个 LSTM 层。
model = Sequential()
model.add(LSTM(input_dim=1, output_dim=hidden_neurons, return_sequences=False))
model.add(RepeatVector(10))
model.add(LSTM(output_dim=hidden_neurons, return_sequences=True))
model.add(TimeDistributed(Dense(1)))
model.add(Activation('linear'))
model.compile(loss='mean_squared_error', optimizer='rmsprop')
预测现在看起来更好,看起来像这样: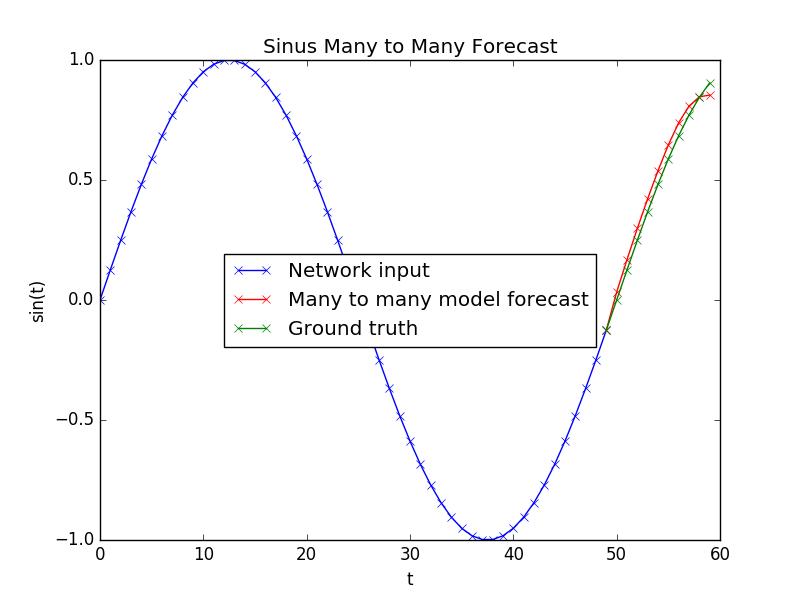
更多推荐
 已为社区贡献126445条内容
已为社区贡献126445条内容







所有评论(0)