【Unity Shader Graph 使用与特效实现】专栏-直达

Arccosine节点是Unity URP Shader Graph中一个重要的数学运算节点，用于计算输入值的反余弦函数。在计算机图形学和着色器编程中，反三角函数在角度计算、向量方向分析、光照模型构建等方面具有广泛的应用。该节点能够处理各种维度的向量输入，包括float、float2、float3和float4类型，为着色器开发提供了强大的数学工具支持。

反余弦函数是余弦函数的反函数，它能够将余弦值映射回对应的角度值。在Shader Graph中，Arccosine节点的实现基于标准的数学库函数，确保了计算的准确性和效率。理解并熟练运用这个节点，对于创建复杂的视觉效果和实现精确的数学计算至关重要。

数学原理

反余弦函数定义

反余弦函数，记作arccos(x)或acos(x)，定义为余弦函数的反函数。对于任意x ∈ [-1, 1]，arccos(x)返回的角度θ满足cos(θ) = x，其中θ ∈ [0, π]弧度或[0, 180]度。这一数学特性使得Arccosine节点在需要从方向余弦值还原角度信息的场景中特别有用。

从几何角度理解，反余弦函数可以看作是单位圆上某点的x坐标与该点和原点连线与正x轴夹角之间的关系。当我们在着色器中处理法线向量、光照方向或反射向量时，这种角度关系变得尤为重要。

定义域和值域特性

Arccosine节点的输入值有严格的定义域限制，输入向量的每个分量必须在[-1, 1]范围内。如果输入值超出这个范围，结果将是未定义的，在某些平台上可能导致NaN（非数字）值。输出值的范围被限制在[0, π]弧度内，这对应于[0, 180]度的角度范围。

这种限制在实际应用中具有重要意义。例如，在计算两个向量之间的夹角时，通过点积得到的余弦值自然落在[-1, 1]范围内，可以直接作为Arccosine节点的输入。了解这一特性有助于避免在着色器编程中出现意外的计算错误。

与其他三角函数的关系

Arccosine节点与其他三角函数节点存在密切的数学关系：

• 与Cosine节点的关系：acos(cos(θ)) = θ，对于θ ∈ [0, π]
• 与Arcsine节点的关系：acos(x) = π/2 - asin(x)，对于x ∈ [-1, 1]
• 与Arctangent节点的关系：acos(x) = atan2(√(1-x²), x)，对于x ∈ [-1, 1]

这些关系在复杂的着色器计算中非常有用，当某个三角函数节点不适用时，可以通过数学变换使用其他节点达到相同的计算目的。

节点描述

功能详解

Arccosine节点的核心功能是计算输入值的反余弦值。当输入为单值浮点数时，节点返回该值的反余弦；当输入为多维向量时，节点会对每个分量独立计算反余弦值，并返回相同维度的结果向量。这种逐分量计算的方式使得节点能够高效处理复杂的向量运算。

在着色器编程中，Arccosine节点通常用于将方向余弦转换回角度值。例如，在光照计算中，我们经常需要知道表面法线与光照方向之间的实际夹角，而不仅仅是它们的点积结果。通过使用Arccosine节点，我们可以从点积得到的余弦值中提取出精确的角度信息。

输入输出特性

Arccosine节点的输入输出具有以下重要特性：

• 输入值自动钳制：虽然理论上输入应在[-1, 1]范围内，但某些Shader Graph实现会自动将输入值钳制到这个范围内，防止无效计算
• 分量独立计算：对于向量输入，每个分量的计算完全独立，不会相互影响
• 维度保持：输出向量与输入向量具有相同的维度和长度
• 弧度输出：所有输出值均以弧度为单位，如需角度值需要额外进行弧度到角度的转换

理解这些特性对于正确使用Arccosine节点至关重要。特别是在处理边界值时，了解系统的自动钳制行为可以避免潜在的计算错误。

性能考虑

在性能方面，Arccosine节点的计算开销相对较高，特别是在移动平台或需要处理大量数据的场景中。反余弦函数的计算通常涉及级数展开或查找表，比基本的算术运算要复杂得多。因此，在性能敏感的应用中，应考虑以下优化策略：

• 尽量避免在片段着色器中频繁使用Arccosine节点
• 考虑使用预计算的值或近似公式替代精确计算
• 在可能的情况下，使用更简单的数学关系避免反三角函数的计算

端口详解

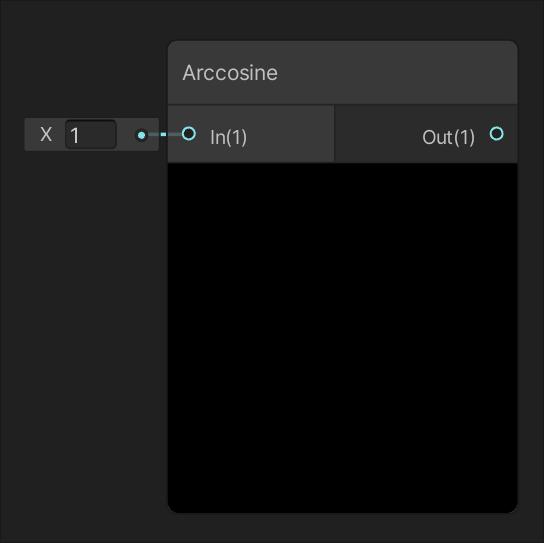
输入端口

Arccosine节点的输入端口标记为"In"，接受动态矢量类型的数据。动态矢量意味着该端口可以连接各种维度的向量数据，系统会根据实际连接的数据类型自动调整内部处理逻辑。

输入端口的设计考虑了Shader Graph的灵活性和易用性：

• 类型自适应：无需手动指定输入维度，系统自动检测连接的数据类型
• 范围验证：在某些Shader Graph版本中，编辑器会提供视觉提示或警告当检测到可能的输入越界
• 多数据源兼容：可以连接常数、属性、纹理采样结果或其他数学节点的输出

在实际使用中，应确保连接到输入端口的值在有效范围内。常见的做法是在连接前使用Clamp节点或Saturate节点对输入值进行限制，确保计算的安全性。

输出端口

输出端口标记为"Out"，同样支持动态矢量类型。输出数据的维度始终与输入数据保持一致，每个分量包含对应输入分量的反余弦值。

输出端口的特点包括：

• 维度一致性：输出向量与输入向量具有相同的结构
• 弧度单位：所有输出值均以弧度为单位，这是计算机图形学中的标准角度表示方式
• 实时计算：输出值根据输入实时计算，没有帧延迟或缓存

当需要角度值而非弧度值时，可以在输出后连接一个乘法节点，将弧度值乘以57.2958（180/π）转换为角度值。这种转换在需要与角度制UI或参数交互时特别有用。

端口连接实践

在实际的Shader Graph构建中，正确连接Arccosine节点的端口需要遵循一些最佳实践：

• 确保上游节点提供有效范围内的值
• 使用适当的节点预处理数据，如Normalize节点确保向量长度为1
• 在下游使用适当的后处理节点，如将弧度转换为角度或进行进一步的数学运算
• 在复杂的数据流中，使用注释说明端口的预期输入和输出，提高可读性

生成代码分析

代码结构解析

Arccosine节点生成的代码体现了简洁高效的设计理念。以float4类型的实现为例：

HLSL

void Unity_Arccosine_float4(float4 In, out float4 Out)
{
    Out = acos(In);
}

这段代码展示了几个重要特点：

• 函数命名规范：遵循Unity_Arccosine_类型的命名约定，清晰表明功能
• 参数设计：使用out参数直接输出结果，避免返回值带来的拷贝开销
• 内部实现：直接调用HLSL内置的acos函数，确保最佳性能和正确性

对于不同维度的向量，Shader Graph会生成相应版本的函数，如Unity_Arccosine_float、Unity_Arccosine_float2、Unity_Arccosine_float3等，确保每种数据类型都能得到正确处理。

HLSL的acos函数

Unity Arccosine节点底层调用的的是HLSL标准库中的acos函数。该函数遵循IEEE标准，提供了高精度的反余弦计算。在大多数现代GPU上，acos函数通过专门的硬件指令实现，保证了计算效率。

HLSL的acos函数具有以下特性：

• 精度：提供完整的单精度浮点数精度
• 异常处理：对超出范围的输入返回未定义结果（通常是NaN）
• 性能优化：在支持的硬件上使用专用数学单元

了解底层实现有助于在需要自定义反余弦计算时（如特定精度的近似计算）做出合适的选择。

自定义实现扩展

虽然Shader Graph提供了标准的Arccosine节点，但在某些特殊情况下可能需要自定义实现。例如，当需要特定的精度优化或特殊的功能扩展时，可以通过Custom Function节点创建自定义的反余弦计算。

常见的自定义实现包括：

• 多项式近似：使用切比雪夫多项式或泰勒级数展开提供更快的计算速度
• 查找表方法：通过预计算的查找表平衡精度和性能
• 特定范围优化：针对已知的输入范围进行特殊优化

这些自定义方法在性能极度敏感或具有特殊计算需求的场景中非常有用。

实际应用案例

向量夹角计算

计算两个向量之间的夹角是Arccosine节点最典型的应用场景。在光照模型、物理渲染和几何处理中，经常需要知道两个方向之间的角度关系。

实现步骤：

• 使用Dot Product节点计算两个归一化向量的点积
• 点积结果即为两向量夹角的余弦值
• 将点积结果输入Arccosine节点得到实际夹角（弧度）

示例应用：

HLSL

// 计算表面法线与光照方向的夹角
float3 normal = normalize(Normal);
float3 lightDir = normalize(LightDirection);
float cosTheta = dot(normal, lightDir);
float angle = acos(cosTheta); // 通过Arccosine节点实现

这种计算在Lambert光照模型、边缘检测和角度相关的材质效果中非常常见。

球形映射与坐标转换

在环境映射和球形纹理映射中，Arccosine节点用于将笛卡尔坐标转换为球面坐标。球面坐标使用两个角度（极角和方位角）来描述三维空间中的方向。

转换过程：

• 极角θ通过Arccosine节点计算：θ = acos(y)，其中y是归一化向量的y分量
• 方位角φ通过Arctangent节点计算：φ = atan2(z, x)

应用场景：

• 环境映射的坐标计算
• 球形纹理映射
• 天空盒和全景图渲染
• 方向性特效的生成

角度限制与范围控制

在游戏开发和视觉效果中，经常需要将角度限制在特定范围内。Arccosine节点可以与其他数学节点结合，实现复杂的角度约束逻辑。

典型应用：

• 关节旋转限制：通过计算当前角度并与限制值比较
• 摄像机视角约束：限制摄像机的俯仰角范围
• 特效方向控制：确保粒子或特效在预期的角度范围内发射

实现模式通常涉及将当前方向转换为角度，应用约束条件，然后再转换回方向向量。

高级光照计算

在基于物理的渲染中，Arccosine节点用于各种高级光照计算：

• Fresnel效应计算：根据视角与表面法线的夹角调整反射强度
• 边缘光照效果：在掠射角增强光照或特效
• 各向异性材质：处理方向相关的反射特性
• 阴影计算：基于角度调整阴影的柔和度

这些应用充分利用了反余弦函数在角度相关计算中的精确性，实现了更加真实和自然的视觉效果。

与其他节点的配合使用

与三角函数节点的组合

Arccosine节点与其他三角函数节点（Sine、Cosine、Tangent及其反函数）可以组合使用，解决复杂的几何和数学问题：

• 角度转换链：acos(cos(θ))用于角度标准化
• 三角恒等式实现：如实现sin(acos(x)) = √(1-x²)
• 坐标系统转换：在极坐标、球面坐标和笛卡尔坐标之间转换

这些组合在解决特定数学问题时非常有效，特别是当直接计算不可行或效率低下时。

与数学节点的协同

Arccosine节点与基本数学节点的协同工作构成了复杂计算的基础：

• 与Clamp节点：确保输入值在有效范围内
• 与Multiply节点：进行弧度到角度的转换
• 与Divide节点：实现角度归一化
• 与Add/Subtract节点：调整角度偏移或范围

通过合理的节点组合，可以实现从简单到复杂的各种数学运算和逻辑控制。

在条件逻辑中的应用

Arccosine节点的输出经常用于驱动条件逻辑和分支判断：

• 角度阈值检测：当夹角小于特定值时触发效果
• 方向分类：根据角度范围将方向分类为不同类别
• 渐进效果：使用角度值驱动平滑的过渡效果

与Branch节点、Compare节点或Step节点结合，可以创建基于角度的智能着色器行为。

最佳实践与注意事项

输入验证与安全

确保Arccosine节点的输入在有效范围内是避免计算错误的关键：

• 始终对输入向量进行归一化处理，确保点积结果在[-1, 1]范围内
• 使用Clamp节点明确限制输入范围，提高代码的鲁棒性
• 在可能产生数值误差的场景中，添加小的容差值

HLSL

// 安全的点积计算与反余弦转换
float3 dirA = normalize(VectorA);
float3 dirB = normalize(VectorB);
float dotProduct = dot(dirA, dirB);
float safeDot = clamp(dotProduct, -1.0, 1.0); // 确保在有效范围内
float angle = acos(safeDot);

性能优化策略

在性能敏感的应用中，优化Arccosine节点的使用：

• 避免在片段着色器中不必要的反余弦计算
• 考虑在顶点着色器或CPU端预计算角度值
• 使用近似公式替代精确计算，当精度要求不高时
• 利用GPU的并行计算特性，批量处理角度计算

对于移动平台或VR应用，这些优化策略尤为重要。

精度与误差管理

理解和管理反余弦计算的精度特性：

• 在角度接近0或π时，反余弦计算对输入误差更敏感
• 对于关键应用，考虑使用双精度计算或误差补偿技术
• 了解目标平台的浮点数精度特性，制定相应的精度策略

在需要高精度角度计算的应用中，如科学可视化或工程模拟，精度管理变得尤为重要。

故障排除与调试

常见问题分析

使用Arccosine节点时可能遇到的典型问题：

• NaN结果：通常由输入超出[-1, 1]范围引起
• 意外角度值：可能由于向量未归一化或坐标系统不匹配
• 性能问题：在复杂着色器中过度使用反余弦计算
• 视觉瑕疵：精度不足或数值不稳定导致

调试技巧与方法

有效的调试策略可以帮助快速定位问题：

• 使用Color节点可视化中间结果，检查数值范围
• 逐步简化节点网络，隔离问题来源
• 使用Preview节点实时监控数值变化
• 对比CPU端计算与GPU端计算的结果差异

Unity Shader Graph提供的实时预览和调试工具大大简化了这些调试过程。

平台兼容性考虑

不同平台对反余弦计算的支持可能存在差异：

• 移动平台的精度和性能限制
• 不同GPU架构的数学单元差异
• 着色器模型支持的特性变化
• 驱动程序级别的优化差异

进行多平台测试是确保着色器在各种设备上正确运行的关键步骤。

---

【Unity Shader Graph 使用与特效实现】专栏-直达
（欢迎点赞留言探讨，更多人加入进来能更加完善这个探索的过程，🙏）