【Unity Shader Graph 使用与特效实现】专栏-直达

在Unity URP Shader Graph中，Matrix Determinant（矩阵行列式）节点是一个强大的数学工具，用于计算输入矩阵的行列式值。这个节点在图形编程和着色器开发中扮演着重要角色，特别是在处理空间变换、体积计算和线性代数运算时。矩阵行列式不仅仅是数学上的一个概念，它直接关联到图形变换中的缩放因子、方向判断以及各种几何属性的计算。

行列式的概念源于线性代数，它能够提供关于矩阵变换特性的重要信息。在三维图形学中，每个变换矩阵都有一个对应的行列式值，这个值可以告诉我们该变换对空间体积的影响程度。当行列式为正值时，表示变换保持了坐标系的方向；当为负值时，表示变换反转了坐标系的方向；而当行列式为零时，表示变换将空间压缩到了更低的维度。

Shader Graph中的Matrix Determinant节点封装了复杂的行列式计算过程，使得着色器开发者无需手动实现这些数学运算，大大简化了着色器的开发流程。无论是处理模型变换、视图变换还是投影变换，该节点都能快速提供关键的行列式信息，帮助开发者实现更加精确和高效的图形效果。

描述

Matrix Determinant节点的核心功能是计算输入矩阵的行列式值。从数学角度来看，行列式是一个标量值，它包含了矩阵所代表线性变换的重要几何信息。在图形学中，这个值可以理解为矩阵描述的变换对空间的缩放因子。

当我们在着色器中使用变换矩阵时，行列式能够告诉我们这个变换对体积的影响程度。例如，如果一个变换矩阵的行列式值为2，这意味着该变换将空间的体积扩大了两倍；如果行列式值为0.5，则表示体积缩小了一半；如果行列式值为负，则表明变换包含了反射操作，改变了坐标系的手性。

在Shader Graph中，Matrix Determinant节点支持多种维度的矩阵输入，包括2x2、3x3和4x4矩阵。无论输入哪种维度的矩阵，输出始终是一个浮点数值，即该矩阵的行列式。这种设计使得节点非常灵活，可以适应各种不同的应用场景。

行列式的计算基于严格的数学定义。对于2x2矩阵，行列式计算相对简单；而对于更高维度的矩阵，计算过程会变得更加复杂。Shader Graph底层通过优化的算法来处理这些计算，确保在着色器执行时能够高效地获取结果。

理解行列式的几何意义对于有效使用这个节点至关重要。除了作为缩放因子外，行列式还可以用于判断矩阵是否可逆（行列式不为零的矩阵是可逆的），计算变换后的面积或体积比例，以及检测坐标系的方向变化等。

端口

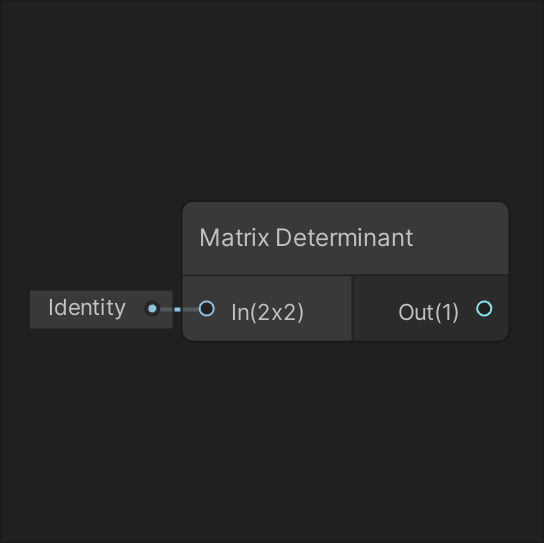
Matrix Determinant节点的端口设计简洁而高效，遵循了Shader Graph节点的一般设计原则。通过有限的端口实现了强大的功能，使得节点既易于使用又功能全面。

输入端口

输入端口是节点接收数据的入口，Matrix Determinant节点只有一个输入端口，标记为"In"。

• 名称：In
• 方向：输入
• 类型：动态矩阵
• 绑定：无
• 描述：接受需要计算行列式的矩阵

输入端口的设计体现了节点的灵活性。所谓的"动态矩阵"意味着该端口可以接受不同维度的矩阵输入，包括2x2、3x3和4x4矩阵。这种动态类型系统是Shader Graph的一个重要特性，它允许同一个节点处理不同类型的数据，减少了需要记忆的节点数量。

在实际使用中，用户可以将任何矩阵值连接到这个输入端口。这个矩阵可以来自Shader Graph中的其他节点，如Matrix Construction节点、变换矩阵节点，或者是通过自定义函数生成的矩阵。输入矩阵的数据来源多种多样，为开发者提供了极大的灵活性。

输入端口对数据类型有严格的验证，只接受矩阵类型的输入。如果尝试连接非矩阵类型的数据，Shader Graph会显示连接错误，防止不合理的数据流。这种类型安全检查有助于在编译前捕获潜在的错误，提高开发效率。

输出端口

输出端口是节点处理结果的出口，Matrix Determinant节点只有一个输出端口，标记为"Out"。

• 名称：Out
• 方向：输出
• 类型：Float
• 绑定：无
• 描述：输出输入矩阵的行列式值

输出端口提供了一个浮点数值，即输入矩阵的行列式。无论输入矩阵的维度如何，输出始终是单个浮点数，这反映了行列式的数学本质——它是一个标量值，不依赖于矩阵的表示形式。

输出值具有明确的数学意义和几何解释。当行列式值为正时，表示变换保持了坐标系的方向；为负时表示方向反转；为零时表示变换是奇异的，即不可逆的。这些特性在着色器编程中非常有用，可以用于实现各种高级效果。

输出端口可以连接到任何接受浮点数输入的节点，如数学运算节点、条件判断节点、材质参数节点等。这种连接灵活性使得Matrix Determinant节点可以轻松集成到复杂的着色器网络中，与其他节点协同工作。

端口间的数据流

理解端口间的数据流对于有效使用Matrix Determinant节点至关重要。数据从输入端口流入，经过节点的内部处理，然后从输出端口流出。

当矩阵数据通过输入端口进入节点时，节点会立即计算其行列式值。这个计算过程是即时的，不依赖于帧率或其他的时间因素。计算完成后，结果会立即通过输出端口提供，供后续节点使用。

数据流的效率是Shader Graph的一个重要考量。Matrix Determinant节点的计算经过高度优化，即使在移动设备上也能快速执行。这使得它适合用于实时图形应用，包括游戏和交互式媒体。

在复杂的着色器图中，Matrix Determinant节点可能只是数据流中的一个环节。它的输出可能被多个其他节点使用，或者经过进一步处理后再影响最终的渲染结果。理解这种数据流有助于构建更加高效和可维护的着色器。

生成的代码示例

Shader Graph节点最终会被编译为实际的着色器代码。理解生成的代码有助于深入掌握节点的工作原理，并在需要时进行自定义或优化。

基本代码结构

Matrix Determinant节点生成的代码遵循HLSL（High Level Shading Language）的标准，这是Unity着色器编程的主要语言。对于最常见的4x4矩阵输入，生成的代码通常如下所示：

HLSL

void Unity_MatrixDeterminant_float4x4(float4x4 In, out float Out)
{
    Out = determinant(In);
}

这段代码定义了一个函数，该函数接受一个4x4矩阵作为输入，并输出一个浮点数值。函数内部调用了HLSL内置的determinant函数，这是HLSL标准库的一部分，专门用于计算矩阵的行列式。

函数命名遵循了Unity Shader Graph的约定：Unity_MatrixDeterminant_float4x4表明这是用于4x4矩阵的行列式计算函数。对于不同维度的矩阵，函数名会相应变化，例如对于3x3矩阵会是Unity_MatrixDeterminant_float3x3。

不同矩阵维度的实现

虽然4x4矩阵在图形学中最为常见，但Matrix Determinant节点也支持其他维度的矩阵。对于不同维度的输入，生成的代码会有所差异。

对于3x3矩阵，生成的代码可能是：

HLSL

void Unity_MatrixDeterminant_float3x3(float3x3 In, out float Out)
{
    Out = determinant(In);
}

对于2x2矩阵，生成的代码可能是：

HLSL

void Unity_MatrixDeterminant_float2x2(float2x2 In, out float Out)
{
    Out = determinant(In);
}

尽管函数名和参数类型不同，但核心计算都是通过HLSL的determinant函数完成的。这表明Shader Graph充分利用了HLSL的内置功能，确保了计算的准确性和效率。

底层实现原理

了解determinant函数的底层实现有助于理解Matrix Determinant节点的性能特征和限制。在HLSL中，determinant函数是内置的，通常由图形驱动程序提供高度优化的实现。

对于2x2矩阵，行列式计算相对简单，公式为：

det([[a, b], [c, d]]) = a*d - b*c

对于3x3矩阵，计算变得复杂一些，使用Sarrus规则或拉普拉斯展开：

det([[a, b, c], [d, e, f], [g, h, i]]) = a*(e*i - f*h) - b*(d*i - f*g) + c*(d*h - e*g)

对于4x4矩阵，计算更加复杂，通常通过分块或展开为多个3x3行列式的组合来计算。

现代GPU对这些计算有专门的硬件优化，因此即使在片段着色器中频繁使用，性能影响通常也是可控的。

自定义实现的可能性

虽然Shader Graph自动生成这些代码，但了解其结构后，开发者可以在需要时创建自定义节点或直接编写着色器代码来实现特殊需求。例如，如果需要对行列式计算过程进行修改或添加调试信息，可以直接在着色器代码中实现类似功能。

以下是一个添加了调试信息的自定义行列式计算函数：

HLSL

void Custom_MatrixDeterminant_float4x4(float4x4 In, out float Out, out bool IsSingular)
{
    Out = determinant(In);
    IsSingular = (Out == 0.0);
}

这个自定义函数不仅计算行列式，还输出一个布尔值指示矩阵是否是奇异的（行列式为零）。这种扩展功能在Shader Graph标准节点中是不可用的，但通过自定义节点或直接编码可以实现。

性能考量

在实时图形应用中，性能始终是一个重要考量。Matrix Determinant节点的性能特征主要取决于输入矩阵的维度和目标硬件平台。

• 低维度矩阵（2x2、3x3）的行列式计算非常快速，通常可以在一个时钟周期内完成
• 高维度矩阵（4x4）的计算需要更多运算，但现代GPU仍有专门优化
• 在顶点着色器中使用通常比在片段着色器中更高效，因为顶点着色器的执行频率通常更低
• 如果可能，应考虑缓存计算结果，避免在同一帧中重复计算相同矩阵的行列式

理解这些性能特征有助于在保持视觉效果的同时优化着色器性能。

实际应用案例

Matrix Determinant节点在着色器开发中有多种实际应用。通过具体案例可以更好地理解如何在实际项目中利用这个节点。

体积缩放计算

一个常见的应用是计算变换对体积的缩放程度。在3D图形中，我们经常需要知道一个变换对物体体积的影响程度，例如在实现某些物理效果或优化渲染时。

HLSL

// 计算模型变换对体积的缩放
float4x4 modelMatrix = GetLocalToWorldMatrix();
float volumeScale = Unity_MatrixDeterminant_float4x4(modelMatrix);

// 根据体积缩放调整效果
if(volumeScale > 1.0)
{
    // 体积放大时的处理
}
else if(volumeScale < 1.0)
{
    // 体积缩小时的处理
}

这种应用在粒子系统、体积雾等效果中特别有用，可以根据变换的缩放程度调整效果的强度或范围。

方向性检测

行列式的符号可以用于检测变换是否包含了反射操作，这在处理法线变换或双面材质时非常有用。

HLSL

// 检测变换是否包含反射
float4x4 viewMatrix = GetWorldToViewMatrix();
float det = Unity_MatrixDeterminant_float4x4(viewMatrix);

// 根据行列式符号调整法线处理
if(det < 0.0)
{
    // 变换包含反射，需要特殊处理法线
    normal = -normal;
}

这种技术可以确保在镜像或反射变换下，光照计算仍然正确。

矩阵可逆性检查

在需要矩阵求逆的操作前，通常需要检查矩阵是否可逆。行列式为零的矩阵是奇异的，不可逆。

HLSL

// 检查矩阵是否可逆
float4x4 transformMatrix = GetSomeTransformMatrix();
float det = Unity_MatrixDeterminant_float4x4(transformMatrix);

if(abs(det) > 1e-6) // 避免浮点精度问题
{
    // 矩阵可逆，安全进行求逆操作
    float4x4 inverseMatrix = inverse(transformMatrix);
    // 使用逆矩阵...
}
else
{
    // 矩阵奇异，使用备选方案
}

这种检查可以防止在奇异矩阵上执行无效的求逆操作，提高着色器的稳定性。

自适应细节级别

在渲染远处物体或小物体时，可以使用行列式来动态调整细节级别，优化性能。

HLSL

// 根据变换的缩放程度调整细节级别
float4x4 modelViewMatrix = mul(GetWorldToViewMatrix(), GetLocalToWorldMatrix());
float scaleFactor = abs(Unity_MatrixDeterminant_float4x4(modelViewMatrix));

// 根据缩放因子选择细节级别
if(scaleFactor < 0.1)
{
    // 使用低细节版本
}
else if(scaleFactor < 1.0)
{
    // 使用中等细节版本
}
else
{
    // 使用高细节版本
}

这种技术可以在保持视觉质量的同时显著提高渲染性能。

最佳实践和注意事项

为了充分发挥Matrix Determinant节点的潜力，同时避免常见陷阱，以下是一些最佳实践和注意事项。

性能优化

• 尽量避免在片段着色器中频繁计算复杂矩阵的行列式，特别是对于4x4矩阵
• 如果可能，在顶点着色器中计算行列式并通过插值传递给片段着色器
• 考虑缓存计算结果，特别是在同一帧中多次使用相同矩阵的行列式时
• 对于静态或变化不频繁的矩阵，可以将行列式预计算并作为uniform变量传递

数值稳定性

• 注意浮点数精度问题，特别是在判断行列式是否为零时
• 使用适当的容差值而不是直接与零比较：abs(det) < epsilon
• 对于接近奇异的矩阵，考虑使用伪逆或其他数值稳定方法
• 在极端缩放情况下，行列式值可能超出浮点数的表示范围，需要特殊处理

与其他节点的配合

Matrix Determinant节点很少单独使用，通常需要与其他节点配合才能发挥最大效用。

• 与Conditional节点结合，根据行列式值选择不同的处理路径
• 与Math节点结合，对行列式值进行进一步处理，如取绝对值、对数变换等
• 与Matrix节点结合，构建需要分析的矩阵或基于行列式结果修改矩阵
• 与Custom Function节点结合，实现基于行列式的复杂算法

调试和验证

在开发过程中，正确验证Matrix Determinant节点的行为非常重要。

• 使用Preview节点可视化行列式值，确保其在预期范围内
• 对于已知矩阵，手动计算行列式值与节点输出对比
• 在极端情况下测试节点行为，如单位矩阵、零矩阵、奇异矩阵等
• 使用不同的矩阵维度测试，确保节点在各种情况下都能正确工作

平台兼容性

虽然Matrix Determinant节点在大多数平台上都能正常工作，但仍需注意一些平台特定问题。

• 在移动设备上，复杂矩阵的行列式计算可能比在桌面GPU上更昂贵
• 某些老旧GPU或特定图形API可能对矩阵运算有不同支持程度
• 在WebGL等目标上，需要测试行列式计算的精度和性能
• 跨平台项目应在所有目标平台上验证基于行列式的效果

---

【Unity Shader Graph 使用与特效实现】专栏-直达
（欢迎点赞留言探讨，更多人加入进来能更加完善这个探索的过程，🙏）