💥💥💞💞欢迎来到本博客❤️❤️💥💥

🏆博主优势：🌞🌞🌞博客内容尽量做到思维缜密，逻辑清晰，为了方便读者。

⛳️座右铭：行百里者，半于九十。

📋📋📋本文内容如下：🎁🎁🎁

 ⛳️赠与读者

👨‍💻做科研，涉及到一个深在的思想系统，需要科研者逻辑缜密，踏实认真，但是不能只是努力，很多时候借力比努力更重要，然后还要有仰望星空的创新点和启发点。建议读者按目录次序逐一浏览，免得骤然跌入幽暗的迷宫找不到来时的路，它不足为你揭示全部问题的答案，但若能解答你胸中升起的一朵朵疑云，也未尝不会酿成晚霞斑斓的别一番景致，万一它给你带来了一场精神世界的苦雨，那就借机洗刷一下原来存放在那儿的“躺平”上的尘埃吧。

     或许，雨过云收，神驰的天地更清朗.......🔎🔎🔎

💥1 概述

多无人机追捕-逃逸平面分散式策略研究

一、研究背景与问题定义

研究背景：多无人机协同追捕-逃逸问题属于多智能体动态博弈领域，具有军事防御、边境巡逻、灾难救援等应用场景。传统集中式控制依赖全局信息，存在通信延迟、单点故障等问题。分散式策略通过局部感知与自主决策，可提升系统鲁棒性与适应性。

问题定义：在二维平面中，N架追捕无人机（Pursuers）需协作捕获M架逃逸无人机（Evaders）。逃逸者采用智能躲避策略，追捕者仅能通过局部传感器获取邻域信息。目标为设计分散式控制律，使追捕者在有限时间内成功包围逃逸者。

二、分散式策略设计方法

分散式策略需满足以下条件：

1. 局部感知：无人机仅能获取邻域内其他无人机的位置、速度信息。
2. 自主决策：每架无人机基于局部信息独立计算控制输入。
3. 协同性：通过隐式通信（如运动趋势）或显式通信（如有限带宽消息）实现协作。

典型方法：

1. 基于Voronoi图的策略：
   • 动态Voronoi分区：根据无人机位置实时划分空间，追捕者向自身Voronoi单元内的逃逸者移动。
   • 改进方法：引入障碍感知的缓冲Voronoi图（OABVC），通过膨胀障碍物边界确保避障安全性。
   • 案例：李品品（2025）提出OABVC策略，在仿真中实现100%包围成功率。
2. 基于比例导引律的策略：
   • Leader-Follower架构：指定一架追捕者为Leader，采用比例导引律追踪逃逸者；Follower通过分布式编队控制跟踪Leader。
   • 改进方法：当Follower接近逃逸者时，切换为协同比例导引律，实现同步打击。
   • 案例：李品品（2025）验证该策略在无界环境中的有效性。
3. 基于博弈论的策略：
   • 纳什均衡求解：将追逃问题建模为非零和微分博弈，追捕者与逃逸者通过优化各自性能指标（如距离最小化、能耗最小化）达到动态平衡。
   • 案例：张旭等（2015）通过线性二次型性能指标求解纳什均衡，证明策略在无障碍区中的最优性。
4. 基于强化学习的策略：
   • 多智能体深度强化学习（MADDPG）：追捕者通过集中训练学习协作策略，分布式执行时仅依赖局部观测。
   • 改进方法：引入逃逸者预测网络（TP Net），利用LSTM预测逃逸者轨迹，提升部分可观测条件下的决策精度。
   • 案例：Game of Drones（2025）通过CBC-TP Net实现城市环境中的95%捕获率。

三、关键技术与挑战

1. 部分可观测性处理：
   • 问题：局部感知导致信息不完整，易陷入局部最优。
   • 解决方案：
     • 历史状态融合：通过LSTM网络记忆逃逸者历史轨迹。
     • 注意力机制：利用Multi-head Self-Attention捕捉观测值间的相关性。
2. 动态环境适应性：
   • 问题：障碍物、动态逃逸策略增加不确定性。
   • 解决方案：
     • 自适应环境生成器：在训练中动态生成障碍物布局，提升策略泛化能力。
     • 两阶段奖励优化：先优化距离奖励，再优化捕捉奖励，平衡探索与利用。
3. 通信约束：
   • 问题：有限带宽下如何实现有效协作。
   • 解决方案：
     • 隐式通信：通过运动趋势传递信息（如Voronoi图更新）。
     • 事件触发通信：仅在需要协同时发送消息（如Leader切换）。

四、仿真与实验验证

1. 仿真环境：
   • 工具：Unity3D（物理引擎）、PyTorch（强化学习框架）、MATLAB（博弈论建模）。
   • 场景：包含障碍物的城市环境、无界开放空间、动态逃逸策略。
2. 性能指标：
   • 捕获率：成功包围逃逸者的比例。
   • 收敛时间：从初始状态到捕获所需时间步数。
   • 能耗：无人机执行策略的总推力消耗。
3. 典型结果：
   • 分散式Voronoi策略：在10×10障碍物环境中，10架追捕者平均120步捕获5架逃逸者，成功率98%。
   • MADDPG+TP Net：在城市环境中，3架追捕者平均85步捕获1架逃逸者，成功率95%。
   • 博弈论策略：在无障碍区中，追逃双方达到纳什均衡，追捕者能耗降低20%。

五、应用场景与扩展方向

1. 军事防御：拦截入侵无人机群，保护关键设施。
2. 边境巡逻：追踪非法越境目标，减少人力投入。
3. 灾难救援：定位受困者，同时避开危险区域。

扩展方向：

• 三维空间追逃：将策略扩展至空中或水下环境。
• 异构无人机编队：结合固定翼与旋翼无人机的优势。
• 对抗性逃逸策略：研究更智能的逃逸算法（如深度强化学习驱动）。

📚2 运行结果

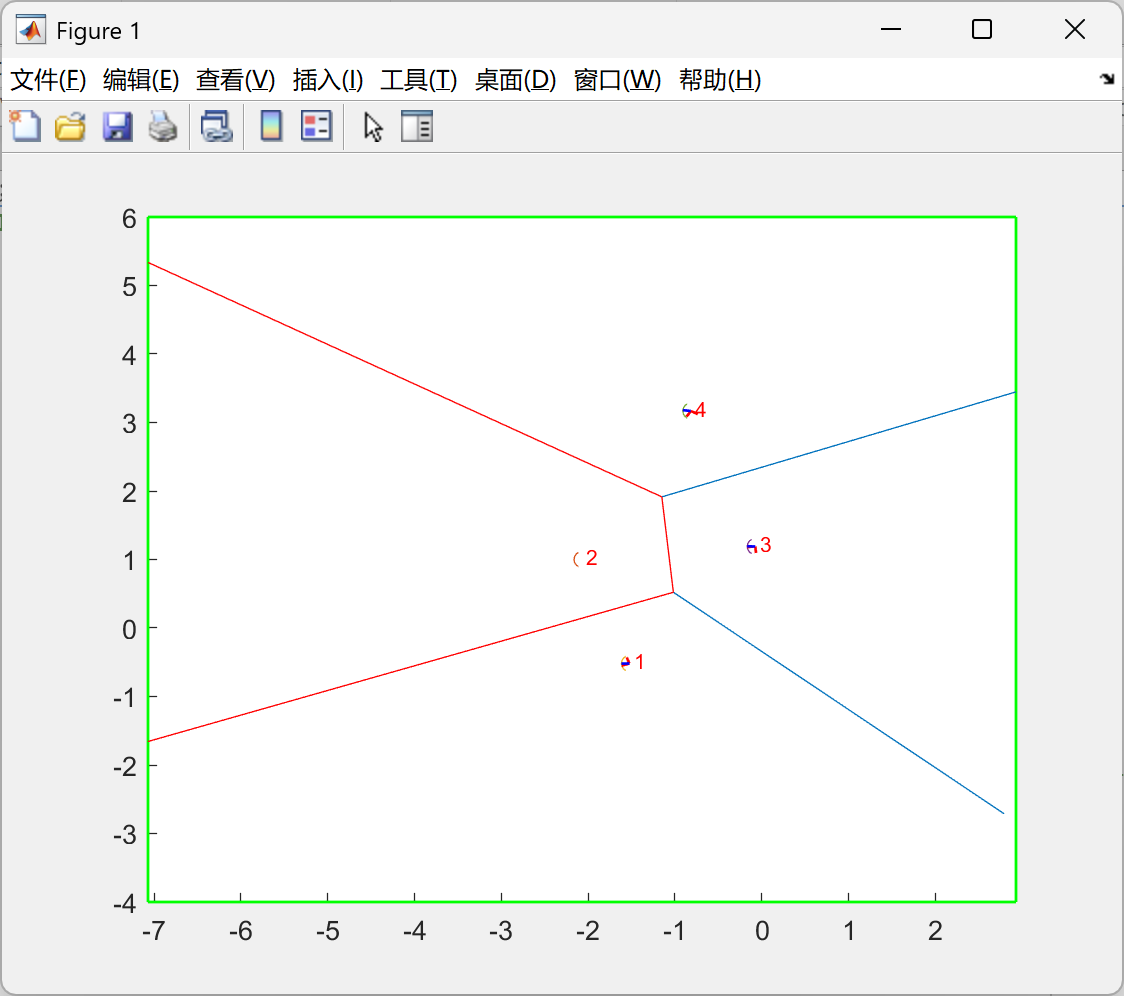
D2_动态有界_虚拟力场控制（VFC）_卡尔曼滤波（KF）：

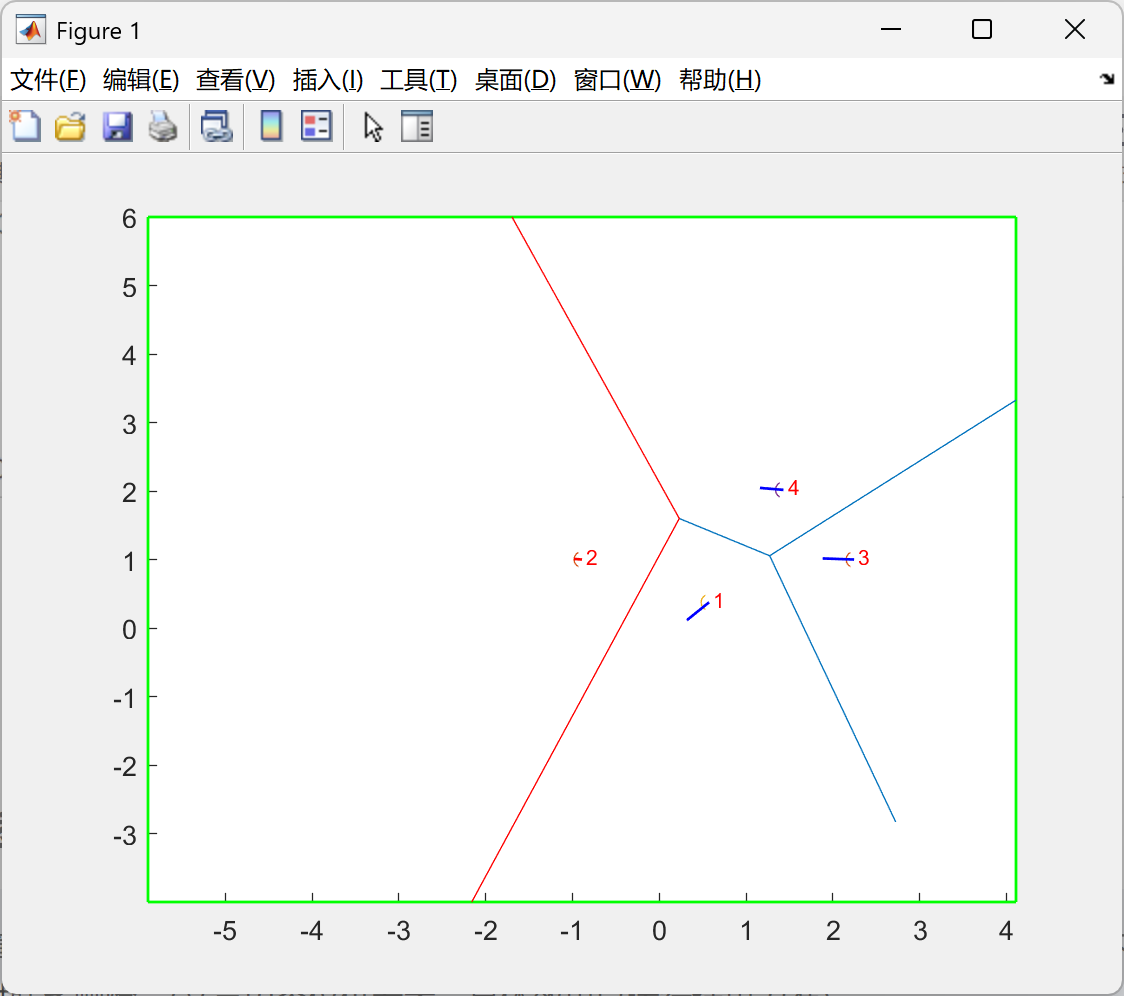
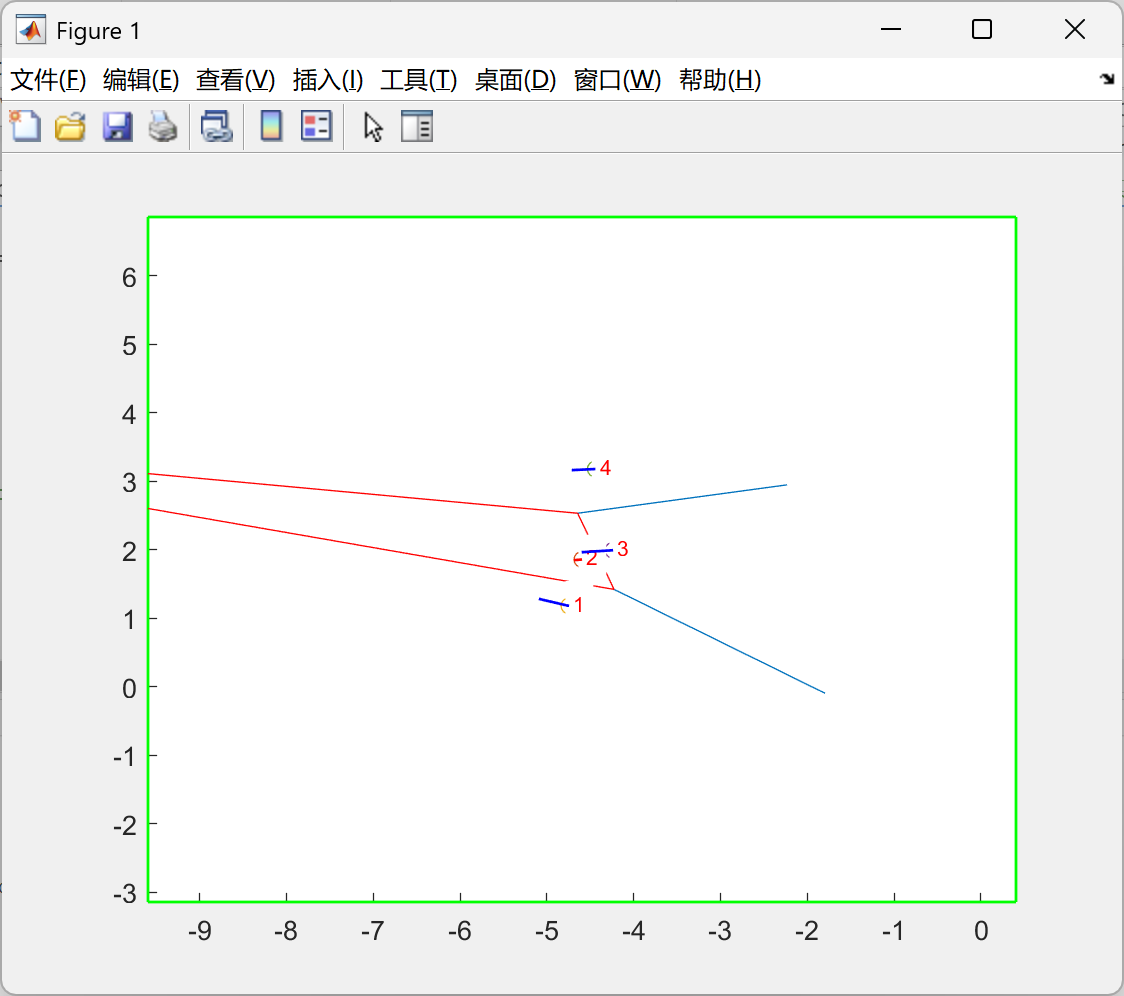
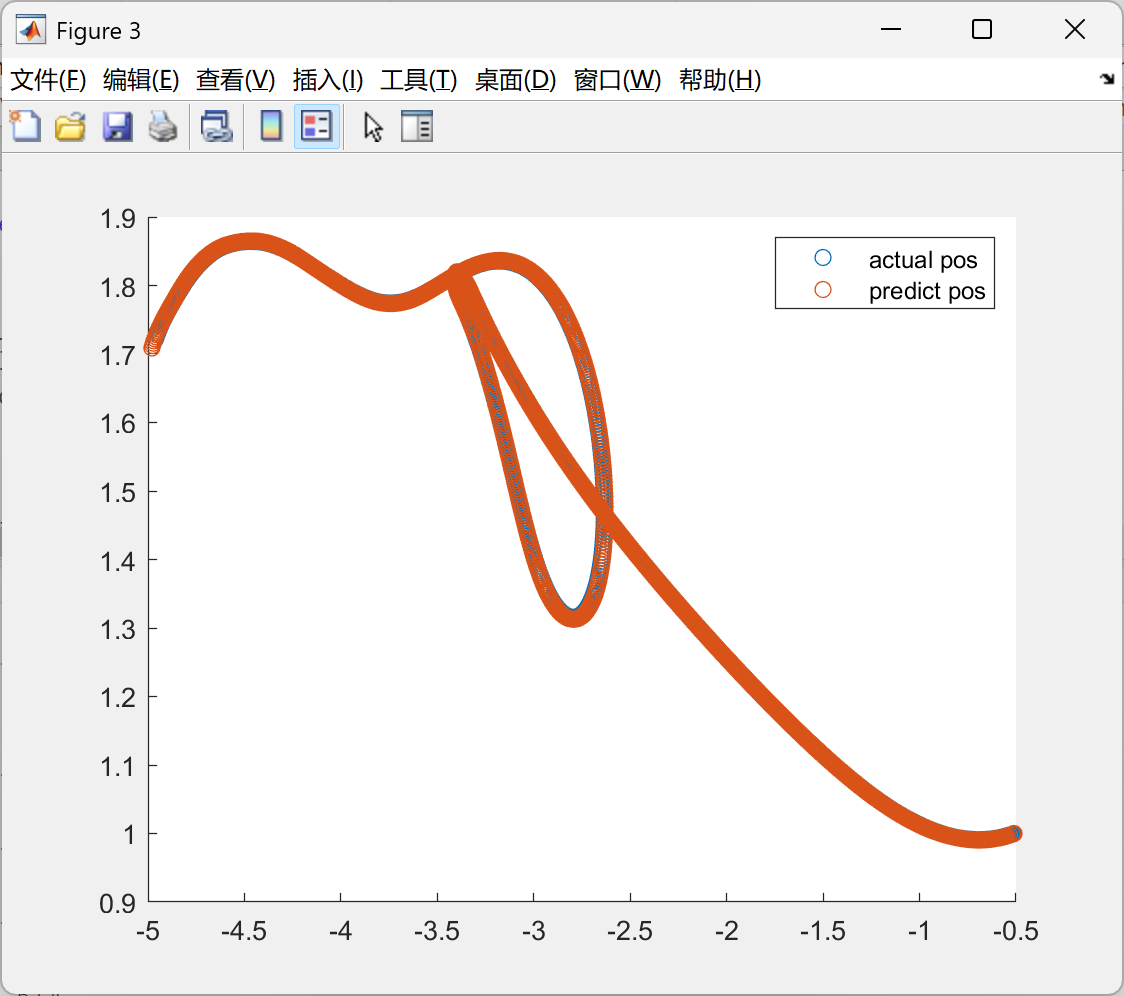
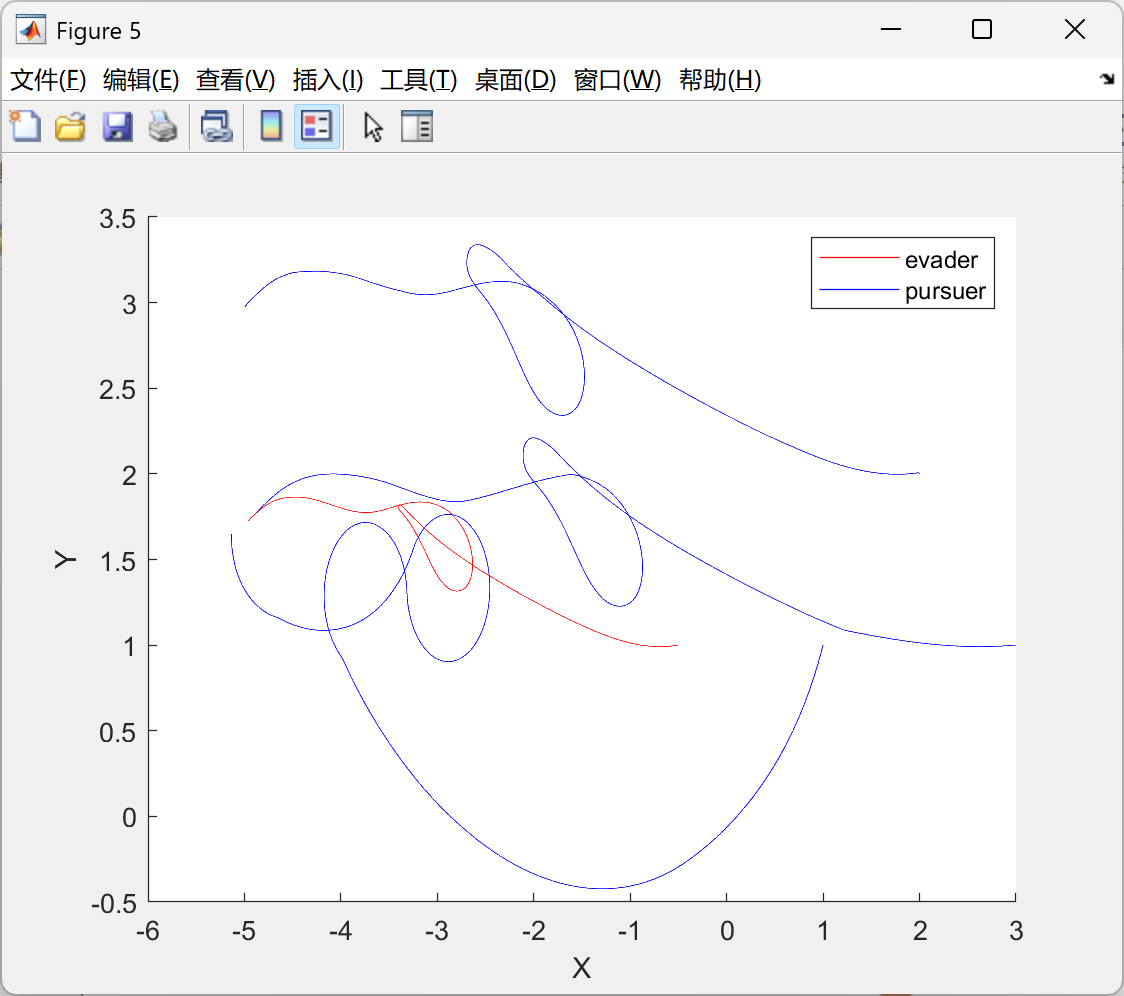
部分代码：

%% run algorithm

while ~captured(P, idx)

e = P(idx, :);

% e_vel = (e_path(T+e_step, :) - e_path(T-1+e_step, :)) * sample_f;

fov = [fov_rel(1:2) + e(1), fov_rel(3:4) + e(2)];

x_min_rel = fov_rel(1) + e(1); x_max_rel = fov_rel(2) + e(1); y_min_rel = fov_rel(3) + e(2); y_max_rel = fov_rel(4) + e(2);

% 给evador分配控制e_vel 给pursuer分配miustar

e_vel = virtualForceControl(P(idx, :), P([1:idx-1, idx+1:end], :), x_max_rel, x_min_rel, y_max_rel, y_min_rel);

e_vel = e_vel * e_slow_scale;

e_vel_pred = e_vel;

% 可以假设直接知道e_vel，也可以用别的方法预测当前时刻evador的速度

xk = KalmanFilter(sample_t, history.velocity, history.position);

e_vel_pred = xk(3:4);

[miu_star, vncomb] = voronoiShrink(P, idx, x_max_rel, x_min_rel, y_max_rel, y_min_rel, e_vel_pred, v_pre, sample_t, wmax, T);

% show result

hold on;

axis(fov);

plot_voronoi(vncomb, P, x_max_rel, x_min_rel, y_max_rel, y_min_rel);

for i = 1:size(P, 1)

% 在点坐标右上方偏移(0.1,0.1)处添加序号

text(P(i,1)+0.05, P(i,2)+0.05, num2str(i), ...

'FontSize', 8, ...

'Color', 'red', ...

'BackgroundColor', 'white', ...

'HorizontalAlignment', 'left');

end

for i = 1 : size(P, 1)

if i == idx

quiver(P(idx, 1), P(idx, 2), e_vel(1)*0.2, e_vel(2)*0.2,'LineWidth', 1, 'Color', 'r', 'MaxHeadSize', 0.1);

else

x0 = P(i, 1); y0 = P(i, 2);

u = miu_star{i}.*0.4;

quiver(x0, y0, u(1), u(2), 'LineWidth', 1, 'Color', 'b', 'MaxHeadSize', 0.1);

end

end

hold off;

% vertexs = [];

% for i = 1 : size(vncomb, 2)

% vertexs = [vertexs; vncomb(i).v1; vncomb(i).v2];

% end

% vertexs = unique(vertexs, 'rows');

% e_A = [e_A, polygonArea(vertexs)];

drawnow;

clf;

% 执行一步控制

for i = 1 : size(P, 1)

if i ~= idx

P(i, :) = P(i, :) + sample_t * miu_star{i};

v_pre(i, :) = miu_star{i};

else

e_step = e_step + 1;

e_step = mod(e_step, size(e_path, 1));

P(i, :) = P(i, :) + e_vel * sample_t;

v_pre(i, :) = e_vel;

end

end

history.velocity(end + 1, :) = e_vel; his_vel_plot(end+1, :) = e_vel; his_pos_pred_plot(end+1, :) = xk(1:2);

history.position(end + 1, :) = P(idx, :); his_e_pos_plot(end+1, :) = P(idx, :); his_vel_pred_plot(end+1, :) = xk(3:4);

refreshHistory(history);

his_all_pos_plot(:, end+1, :) = P;

T = T + 1;

end

%% show kalman filter

figure(3);

hold on;

x = 1 : T;

scatter(his_e_pos_plot(3:end, 1), his_e_pos_plot(3:end, 2));

scatter(his_pos_pred_plot(:, 1), his_pos_pred_plot(:, 2));

% his_vel_plot = his_pos_plot * sample_t; his_pos_pred_plot

% quiver(his_pos_pred_plot(3:end, 1))

legend("actual pos", "predict pos");

hold off;

figure(4);

diff = his_vel_pred_plot - his_vel_plot(3:end, :);

diff_len = zeros(size(diff, 1), 1);

for i = 1 : size(diff, 1)

diff_len(i) = norm(diff(i, :));

end

plot(linspace(0, T*sample_t, size(diff, 1)), diff_len);

figure(5);

hold on;

ph1 = []; ph2 = [];

for i = 1 : size(P, 1)

if i == idx

color = 'red';

ph1 = plot3(his_all_pos_plot(i, :, 1), his_all_pos_plot(i, :, 2), linspace(0, T*sample_t, size(his_all_pos_plot, 2)), 'Color', color);

% legend(ph, 'evader')

else

color = 'blue';

ph2 = plot3(his_all_pos_plot(i, :, 1), his_all_pos_plot(i, :, 2), linspace(0, T*sample_t, size(his_all_pos_plot, 2)), 'Color', color);

% legend(ph, 'pursuer')

end

xlabel("X");ylabel('Y');zlabel('t');

end

legend([ph1, ph2], ["evader", "pursuer"]);

hold off;

🎉3 参考文献 

文章中一些内容引自网络，会注明出处或引用为参考文献，难免有未尽之处，如有不妥，请随时联系删除。(文章内容仅供参考，具体效果以运行结果为准)

🌈4 Matlab代码实现

资料获取，更多粉丝福利，MATLAB|Simulink|Python资源获取